数模笔记模型篇一

线性规划（LP）

一般形式

可行解： 满足约束条件（4）的解 $x = [x_1, \ldots, x_n]^T$ ，称为线性规划问题的可行解，而使目标函数（3）达到最大值的可行解叫最优解。

可行域： 可行解构成的集合称为问题的可行域，记为 $R$

使用 scipy.optimize.linprog 解 LP 的代码模板

25.6.25更新：scipy.optimize.linprog狗都不用，直接用PuLP库太香了

from scipy.optimize import linprog

# 目标函数系数 c（注意是最小化）
c = [cost1, cost2, ..., costn]  # 要求最小化 c^T x

# 不等式约束：Ax ≤ b, 若Ax ≥ b则两边同时取负号−Ax ≤ −b
A = [
    [a11, a12, ..., a1n],
    [a21, a22, ..., a2n],
    ...
]
b = [b1, b2, ..., bm]

# 等式约束：Aeq x = beq（可选）
A_eq = [
    [aeq11, aeq12, ..., aeq1n],
    ...
]
b_eq = [beq1, beq2, ...]

# 变量范围：每个变量 x_i 的 (min, max)
bounds = [(lb1, ub1), (lb2, ub2), ..., (lbn, ubn)]

# 求解
res = linprog(c, A_ub=A, b_ub=b, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method="highs")

# 输出结果
if res.success:
    print("最小值:", res.fun)
    print("最优解 x:", res.x)
else:
    print("求解失败:", res.message)

若求最大值就在目标函数c处加负号

例如：最大化利润 40x + 30y → 最小化 -40x -30y
则 c = [-40, -30]

非线性的有时候也可以转化为线性规划的问题

例题

市场上有 $n$ 种资产 $S_i$ （ $i = 1, 2, \ldots, n$ ）可以选择，现用数额为 $M$ 的相当大的资金作一个时期的投资。这 $n$ 种资产在这一时期内购买 $S_i$ 的平均收益率为 $r_i$ ，风险损失率为 $q_i$ 。投资越分散，总的风险越少，总体风险可用投资的 $S_i$ 中最大的一个风险来度量。

购买 $S_i$ 时要付交易费，费率为 $p_i$ ，当购买额不超过给定值 $u_i$ 时，交易费按购买 $u_i$ 计算。另外，假定同期银行存款利率是 $r_0$ （ $r_0 = 5\%$ ），既无交易费又无风险。

已知 $n = 4$ 时相关数据如下：

资产 $S_i$	收益率 $r_i(\%)$	风险率 $q_i(\%)$	交易费率 $p_i(\%)$	交易费阈值 $u_i$ (元)
$S_1$	28	2.5	1	103
$S_2$	21	1.5	2	198
$S_3$	23	5.5	4.5	52
$S_4$	25	2.6	6.5	40

投资目标
用给定资金 $M$ ，有选择地购买若干种资产或存银行生息（无风险利率 $r_0=5\%$ ），要求：

净收益尽可能大
总体风险（定义为所投资资产中最大单个风险）尽可能小

解答

符号规定

符号	说明
$s_i$	第 $i$ 种投资项目（ $i = 0,1,\ldots,n$ ），其中 $s_0$ 表示存入银行
$r_i$	$s_i$ 的平均收益率（ $i = 0,\ldots,n$ ）
$p_i$	$s_i$ 的交易费率（ $i = 0,\ldots,n$ ），其中 $p_0 = 0$
$q_i$	$s_i$ 的风险损失率（ $i = 0,\ldots,n$ ），其中 $q_0 = 0$
$u_i$	$s_i$ 的交易定额（ $i = 1,\ldots,n$ ）
$x_i$	投资项目 $s_i$ 的资金（ $i = 0,1,\ldots,n$ ）
$a$	投资风险度
$Q$	总体收益

基本假设

投资规模
投资数额 $M$ 相当大，为便于计算，设 $M = 1$ （单位化处理）
风险分散性
投资越分散，总风险越小
风险度量
总体风险定义为所有投资项目 $s_i$ 中最大的单个风险，即 $\max(q_i x_i)$ ，其中 $x_i$ 为投资比例
资产独立性
$n + 1$ 种资产 $s_i$ （含银行存款）之间相互独立
参数稳定性
在投资期内，各资产的参数为定值，不受其他意外因素影响：
- 收益率 $r_i$
- 交易费率 $p_i$
- 风险损失率 $q_i$
收益与风险的决定性
净收益和总体风险仅由 $r_i, p_i, q_i$ 决定，不受其他因素干扰

模型关键定义

总体风险度量
总体风险定义为所投资资产中最大单项风险：
$\max \{ q_i x_i \mid i = 1, 2, \ldots, n \}.$
交易费分段函数
购买资产 $s_i$ ( $i = 1, \ldots, n$ ) 的交易费计算规则：
$\text{交易费} = \begin{cases} p_i x_i, & x_i > u_i; \\ p_i u_i, & x_i \leq u_i. \end{cases}$

简化假设：由于 $u_i$ 和 $p_i u_i$ 相对总投资 $M$ 极小，净收益可近似为 $(r_i - p_i)x_i$
多目标规划性质
目标函数需同时满足：
- 净收益 $(r_i - p_i)x_i$ 最大化
- 总体风险 $\max(q_i x_i)$ 最小化
  （需通过多目标优化方法求解）

总结一下：

\text{目标函数} \begin{cases} \max \sum\limits_{i=0}^n (r_i - p_i)x_i & \text{(最大化净收益)} \\ \min \max \{q_i x_i\} & \text{(最小化最大单项风险)} \end{cases}

\text{约束条件} \begin{cases} \sum\limits_{i=0}^n (1 + p_i)x_i = M & \text{(总资金约束)} \\ x_i \geq 0, & i = 0,1,\cdots,n \end{cases}

多目标转单目标

模型一： 固定风险水平下的收益优化模型

通过引入风险承受界限 $a$ ，将多目标规划转化为单目标线性规划：

限定最大风险： $\max \frac{q_i x_i}{M} \leq a$
单一优化目标：最大化净收益

目标函数

\max \sum_{i=0}^n (r_i - p_i)x_i

约束条件

\begin{cases} \frac{q_i x_i}{M} \leq a, & i=1,\ldots,n \quad \text{(单项风险控制)} \\ \sum\limits_{i=0}^n (1 + p_i)x_i = M, & \text{(资金总量约束)} \\ x_i \geq 0, & i=0,1,\ldots,n \quad \text{(非负投资)} \end{cases}

模型二： 固定收益下的风险最小化

目标函数

\min \{\max \{ q_i x_i \}\}

约束条件

\begin{cases} \sum\limits_{i=0}^n (r_i - p_i)x_i \geq k & \text{(最低收益要求)} \\ \sum\limits_{i=0}^n (1 + p_i)x_i = M & \text{(资金总量约束)} \\ x_i \geq 0, & i=0,1,\ldots,n \end{cases}

模型三： 风险-收益加权优化

投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资组合。因此对风险、收益分别赋予权重 $s$ （ $0 < s \leq 1$ ）和 $(1-s)$ ， $s$ 称为投资偏好系数

目标函数

\min \left[ s \cdot \max \{ q_i x_i \} - (1-s) \sum\limits_{i=0}^n (r_i - p_i)x_i \right]

约束条件

\begin{cases} \sum\limits_{i=0}^n (1 + p_i)x_i = M \\ x_i \geq 0, & i=0,1,\ldots,n \end{cases}

整数规划（ILP）

整数规划特点

原线性规划有最优解，当自变量限制为整数后，其整数规划解出现下述情况

原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致
整数规划无可行解
有可行解（当然就存在最优解），但最优解值变差

整数规划最优解不能按照实数最优解简单取整而获得，可能会超出可行域

整数规划分类:

纯整数规划：所有决策变量要求取非负整数（这时引进的松弛变量和剩余变量可以不要求取整数）
全整数规划：除了所有决策变量要求取非负整数外，系数 $a_{ij}$ 和常数 $b_i$ 也要求取整数（这时引进的松弛变量和剩余变量也必须是整数）
混合整数规划：只有一部分的决策变量要求取非负整数，另一部分可以取非负实数
0—1整数规划：所有决策变量只能取0或1两个整数

松弛变量: $x_1 + x_2 \geq 10$ 引入 $x_3$ → $x_1 + x_2 + x_3 = 10$ ， $x_3 \geq 0$
剩余变量: $x_1 + x_2 \geq 10$ 引入 $x_3$ → $x_1 + x_2 - x_3 = 10$ ， $x_3 \leq 0$
松弛变量和剩余变量的目的是将不等式约束转化为等式约束

整数规划与松弛的线性规划的关系：

整数规划可行解是松弛问题可行域中的整数格点松弛问题无可行解，则整数规划无可行解
ILP最优值小于或等于松弛问题的最优值
松弛问题最优解满足整数要求，则该最优解为整数规划最优解

一般形式

\max(\min) \, z = \sum_{j=1}^n c_j x_j

\begin{cases} \sum_{j=1}^n a_{ij} x_j \leq (=, \geq) b_i & (i = 1, 2, \ldots m) \\ x_j \geq 0, & x_j \text{为整数} \, (j = 1, 2, \ldots n) \end{cases}

分支定界算法 (Deprecated)

不考虑整数限制先求出相应松弛问题的最优解

若不满足整数条件，则任选一个不满足整数条件的变量 $x_i^0$ 来构造新的约束添加到松弛问题中形成两个子问题：

x_i \leq \left\lfloor x_i^0 \right\rfloor

x_i \geq \left\lfloor x_i^0 \right\rfloor + 1

缩小的可行域中求解新构造的线性规划的最优解，并重复上述过程，直到子问题无解或有整数最优解（被查清）

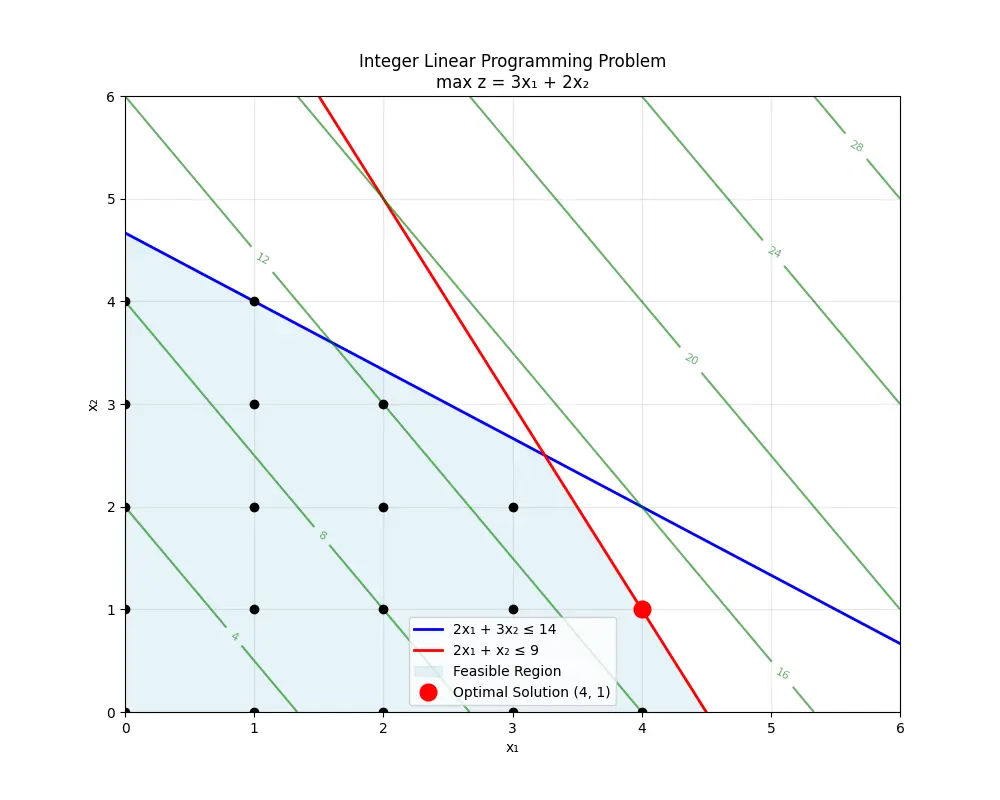
示例:

\max z = 3x_1 + 2x_2

\begin{cases} 2x_1 + 3x_2 \leq 14 \\ 2x_1 + x_2 \leq 9 \\ x_1, x_2 \geq 0 \end{cases}

import numpy as np
from scipy.optimize import linprog
import matplotlib.pyplot as plt
from collections import deque


class BranchAndBoundSolver:
    """分支定界法求解器类"""

    def __init__(self):
        """初始化求解器"""
        self.best_solution = None  # 最优解
        self.best_value = float('-inf')  # 最优目标函数值
        self.nodes_explored = 0  # 已探索节点数

    def solve_lp_relaxation(self, c, A_ub, b_ub, bounds):
        """
        求解线性规划松弛问题
        参数:
            c: 目标函数系数
            A_ub: 不等式约束系数矩阵
            b_ub: 不等式约束右端向量
            bounds: 变量边界
        返回:
            目标函数值, 解向量
        """
        # scipy求最小值，目标函数系数取负数转换为最大值问题
        result = linprog(-c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

        if result.success:
            return -result.fun, result.x  # 返回最大值和解
        else:
            return None, None

    def is_integer_solution(self, x, tolerance=1e-6):
        """检查解是否为整数解"""
        return all(abs(xi - round(xi)) < tolerance for xi in x)

    def find_fractional_variable(self, x, tolerance=1e-6):
        """找到第一个非整数变量的索引"""
        for i, xi in enumerate(x):
            if abs(xi - round(xi)) >= tolerance:
                return i
        return None

    def solve(self, c, A_ub, b_ub, initial_bounds):
        """
        主求解函数 - 分支定界法
        参数:
            c: 目标函数系数
            A_ub: 约束矩阵
            b_ub: 约束右端向量
            initial_bounds: 初始变量边界
        """
        # 用队列存储待处理的节点 (边界, 深度)
        queue = deque([(initial_bounds, 0)])

        print("开始分支定界法求解...")
        print("=" * 50)

        while queue:
            current_bounds, depth = queue.popleft()
            self.nodes_explored += 1

            print(f"\n节点 {self.nodes_explored}:")
            print(f"边界: x1∈{current_bounds[0]}, x2∈{current_bounds[1]}")

            # 求解当前节点的LP松弛
            obj_value, solution = self.solve_lp_relaxation(c, A_ub, b_ub, current_bounds)

            if obj_value is None:
                print("  无可行解")
                continue

            print(f"  LP解: x1={solution[0]:.3f}, x2={solution[1]:.3f}, z={obj_value:.3f}")

            # 剪枝：如果上界不能改进当前最优解
            if obj_value <= self.best_value:
                print(f"  剪枝: {obj_value:.3f} ≤ {self.best_value}")
                continue

            # 检查是否为整数解
            if self.is_integer_solution(solution):
                print("  *** 找到整数解! ***")
                if obj_value > self.best_value:
                    self.best_value = obj_value
                    self.best_solution = solution.copy()
                    print(f"  *** 更新最优解: z={obj_value} ***")
                continue

            # 分支：选择第一个非整数变量
            branch_var = self.find_fractional_variable(solution)
            if branch_var is not None:
                branch_value = solution[branch_var]
                print(f"  分支变量: x{branch_var + 1}={branch_value:.3f}")

                # 创建左右两个子问题
                left_bounds = [list(bound) if isinstance(bound, tuple) else bound for bound in current_bounds]
                right_bounds = [list(bound) if isinstance(bound, tuple) else bound for bound in current_bounds]

                # 左分支: x[branch_var] <= floor(branch_value)
                left_bounds[branch_var] = (left_bounds[branch_var][0], int(branch_value))
                # 右分支: x[branch_var] >= ceil(branch_value)
                right_bounds[branch_var] = (int(branch_value) + 1, right_bounds[branch_var][1])

                # 添加子问题到队列
                queue.append((left_bounds, depth + 1))
                queue.append((right_bounds, depth + 1))

        # 输出最终结果
        print("\n" + "=" * 50)
        print("求解完成!")
        print(f"探索节点数: {self.nodes_explored}")

        if self.best_solution is not None:
            print(f"最优解: x1={int(self.best_solution[0])}, x2={int(self.best_solution[1])}")
            print(f"最优值: z={self.best_value}")
        else:
            print("未找到可行解")

    def visualize_problem(self, c, A_ub, b_ub):
        """
        可视化问题的可行域和解
        参数:
            c: 目标函数系数
            A_ub: 约束矩阵
            b_ub: 约束右端向量
        """
        # 创建图形
        plt.figure(figsize=(10, 8))

        # 定义x1的范围
        x1 = np.linspace(0, 6, 100)

        # 绘制约束线
        # 约束1: 2x1 + 3x2 <= 14
        x2_1 = (14 - 2 * x1) / 3
        plt.plot(x1, x2_1, 'b-', label='2x₁ + 3x₂ ≤ 14', linewidth=2)

        # 约束2: 2x1 + x2 <= 9
        x2_2 = 9 - 2 * x1
        plt.plot(x1, x2_2, 'r-', label='2x₁ + x₂ ≤ 9', linewidth=2)

        # 填充可行域
        x1_fill = np.linspace(0, 4.5, 100)
        x2_fill1 = np.minimum((14 - 2 * x1_fill) / 3, 9 - 2 * x1_fill)
        x2_fill2 = np.zeros_like(x1_fill)
        plt.fill_between(x1_fill, x2_fill2, np.maximum(x2_fill1, 0),
                         alpha=0.3, color='lightblue', label='Feasible Region')

        # 绘制目标函数等值线
        X1, X2 = np.meshgrid(np.linspace(0, 6, 50), np.linspace(0, 6, 50))
        Z = 3 * X1 + 2 * X2
        contours = plt.contour(X1, X2, Z, levels=8, colors='green', alpha=0.6)
        plt.clabel(contours, inline=True, fontsize=8)

        # 标记所有整数点
        for i in range(6):
            for j in range(6):
                if 2 * i + 3 * j <= 14 and 2 * i + j <= 9 and i >= 0 and j >= 0:
                    plt.plot(i, j, 'ko', markersize=6)

        # 标记最优解
        if self.best_solution is not None:
            x1_opt, x2_opt = int(self.best_solution[0]), int(self.best_solution[1])
            plt.plot(x1_opt, x2_opt, 'ro', markersize=12,
                     label=f'Optimal Solution ({x1_opt}, {x2_opt})')

        # 设置图形属性
        plt.xlim(0, 6)
        plt.ylim(0, 6)
        plt.xlabel('x₁')
        plt.ylabel('x₂')
        plt.title('Integer Linear Programming Problem\nmax z = 3x₁ + 2x₂')
        plt.legend()
        plt.grid(True, alpha=0.3)
        plt.show()


def main():
    """主函数 - 定义问题并求解"""

    # 1. 定义问题参数
    print("线性整数规划问题:")
    print("目标函数: max z = 3x₁ + 2x₂")
    print("约束条件:")
    print("  2x₁ + 3x₂ ≤ 14")
    print("  2x₁ + x₂ ≤ 9")
    print("  x₁, x₂ ≥ 0 且为整数")

    # 目标函数系数
    c = np.array([3, 2])

    # 约束矩阵和右端向量
    A_ub = np.array([
        [2, 3],  # 第一个约束: 2x₁ + 3x₂ ≤ 14
        [2, 1]  # 第二个约束: 2x₁ + x₂ ≤ 9
    ])
    b_ub = np.array([14, 9])

    # 变量边界 (下界, 上界)
    initial_bounds = [(0, 10), (0, 10)]

    # 2. 创建求解器并求解
    solver = BranchAndBoundSolver()
    solver.solve(c, A_ub, b_ub, initial_bounds)

    # 3. 可视化结果
    solver.visualize_problem(c, A_ub, b_ub)

    # 4. 验证解的正确性
    if solver.best_solution is not None:
        x1, x2 = int(solver.best_solution[0]), int(solver.best_solution[1])
        print(f"\n解的验证:")

        # 检查约束条件
        constraint1 = 2 * x1 + 3 * x2
        constraint2 = 2 * x1 + x2
        objective = 3 * x1 + 2 * x2

        print(f"约束1: 2×{x1} + 3×{x2} = {constraint1} ≤ 14 ✓" if constraint1 <= 14 else "约束1违反!")
        print(f"约束2: 2×{x1} + 1×{x2} = {constraint2} ≤ 9 ✓" if constraint2 <= 9 else "约束2违反!")
        print(f"目标函数: 3×{x1} + 2×{x2} = {objective}")

        # 5. 与LP松弛解比较
        print(f"\n与LP松弛解的比较:")
        result = linprog(-c, A_ub=A_ub, b_ub=b_ub, bounds=[(0, None), (0, None)], method='highs')
        if result.success:
            lp_solution = result.x
            lp_value = -result.fun
            print(f"LP松弛解: x₁={lp_solution[0]:.3f}, x₂={lp_solution[1]:.3f}")
            print(f"LP松弛值: z={lp_value:.3f}")
            print(f"整数解值: z={objective}")
            print(f"最优性间隙: {lp_value - objective:.3f}")


if __name__ == "__main__":
    main()

输出：

线性整数规划问题:
目标函数: max z = 3x₁ + 2x₂
约束条件:
  2x₁ + 3x₂ ≤ 14
  2x₁ + x₂ ≤ 9
  x₁, x₂ ≥ 0 且为整数
开始分支定界法求解...
==================================================

节点 1:
边界: x1∈(0, 10), x2∈(0, 10)
  LP解: x1=3.250, x2=2.500, z=14.750
  分支变量: x1=3.250

节点 2:
边界: x1∈(0, 3), x2∈[0, 10]
  LP解: x1=3.000, x2=2.667, z=14.333
  分支变量: x2=2.667

节点 3:
边界: x1∈(4, 10), x2∈[0, 10]
  LP解: x1=4.000, x2=1.000, z=14.000
  *** 找到整数解! ***
  *** 更新最优解: z=14.0 ***

节点 4:
边界: x1∈[0, 3], x2∈(0, 2)
  LP解: x1=3.000, x2=2.000, z=13.000
  剪枝: 13.000 ≤ 14.0

节点 5:
边界: x1∈[0, 3], x2∈(3, 10)
  LP解: x1=2.500, x2=3.000, z=13.500
  剪枝: 13.500 ≤ 14.0

==================================================
求解完成!
探索节点数: 5
最优解: x1=4, x2=1
最优值: z=14.0

解的验证:
约束1: 2×4 + 3×1 = 11 ≤ 14 ✓
约束2: 2×4 + 1×1 = 9 ≤ 9 ✓
目标函数: 3×4 + 2×1 = 14

与LP松弛解的比较:
LP松弛解: x₁=3.250, x₂=2.500
LP松弛值: z=14.750
整数解值: z=14
最优性间隙: 0.750

PuLP库

PuLP是一个功能强大的Python库，专门用于解决线性规划、整数规划和混合整数规划问题

示例:

import pulp


def solve_integer_programming_with_pulp():
    """
    使用PuLP求解整数线性规划问题

    问题描述:
    最大化: z = 3x₁ + 2x₂
    约束条件:
        2x₁ + 3x₂ ≤ 14
        2x₁ + x₂ ≤ 9
        x₁, x₂ ≥ 0 且为整数
    """

    # 步骤1: 创建问题实例
    prob = pulp.LpProblem("Integer_Linear_Programming", pulp.LpMaximize)

    # 步骤2: 定义决策变量（整数变量）
    x1 = pulp.LpVariable("x1", lowBound=0, cat='Integer')
    x2 = pulp.LpVariable("x2", lowBound=0, cat='Integer')

    # 步骤3: 添加目标函数
    prob += 3 * x1 + 2 * x2, "Objective_Function"

    # 步骤4: 添加约束条件
    prob += 2 * x1 + 3 * x2 <= 14, "Material_Constraint"
    prob += 2 * x1 + x2 <= 9, "Time_Constraint"

    # 步骤5: 求解问题
    print("Solving the problem...")
    prob.solve(pulp.PULP_CBC_CMD(msg=0))  # msg=0 隐藏求解器详细输出

    # 步骤6: 检查求解状态
    print(f"Status: {pulp.LpStatus[prob.status]}")

    # 步骤7: 输出结果
    if prob.status == pulp.LpStatusOptimal:
        print("\nOptimal Solution Found!")
        print(f"x₁ = {int(x1.varValue)}")
        print(f"x₂ = {int(x2.varValue)}")
        print(f"Maximum objective value z = {int(pulp.value(prob.objective))}")

        # 验证约束条件
        print("\nConstraint Verification:")
        x1_val = int(x1.varValue)
        x2_val = int(x2.varValue)

        constraint1_value = 2 * x1_val + 3 * x2_val
        constraint2_value = 2 * x1_val + x2_val

        print(f"Constraint 1: 2×{x1_val} + 3×{x2_val} = {constraint1_value} ≤ 14 ✓")
        print(f"Constraint 2: 2×{x1_val} + 1×{x2_val} = {constraint2_value} ≤ 9 ✓")

        return x1_val, x2_val, int(pulp.value(prob.objective))
    else:
        print("No optimal solution found!")
        return None

def main():
    solve_integer_programming_with_pulp()

if __name__ == "__main__":
    main()

非线性规划（NP）

一般形式

\min f(x)

\begin{cases} A \cdot x \leq b \\ Aeq \cdot x = beq \\ c(x) \leq 0 \\ ceq(x) = 0 \\ lb \leq x \leq ub \end{cases}

其中：

$f(x)$ 是标量目标函数
$A$ , $b$ , $Aeq$ , $beq$ 是线性约束的矩阵和向量
$c(x)$ , $ceq(x)$ 是非线性约束函数
$lb$ , $ub$ 是变量的下界和上界

Pyomo库

Pyomo作为一个功能强大的Python优化建模语言，能够处理广泛的数学规划问题

具体包括：

线性规划问题

标准线性规划（LP）
混合整数线性规划（MILP）

非线性规划问题

非线性规划（NLP）
混合整数非线性规划（MINLP）
混合整数二次规划（MIQP）

特殊问题类型

二次规划（QP）
随机规划
双层规划问题
广义析取规划
带平衡约束的数学规划
微分代数方程优化问题

安装:

1 2	`pip install pyomo conda install -c conda-forge ipopt`

Pyomo和求解器的安装建议用conda而不是普通的虚拟环境，不然会遇到奇妙bug（

示例代码:

unified_optimization.py

import pyomo.environ as pyo
import numpy as np
import matplotlib.pyplot as plt
from pyomo.opt import SolverStatus, TerminationCondition
import warnings

warnings.filterwarnings('ignore')

# English font setup for all plots
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 10


class OptimizationSolver:

    def __init__(self, name="Problem"):
        self.model = None
        self.solver = None
        self.results = None
        self.name = name
        self.problem_type = "LP"
        self.var_names = []
        self.var_types = []
        self.constraint_counter = 0
        self.has_integer_vars = False
        self.has_continuous_vars = False
        self.has_quadratic_terms = False
        self.has_nonlinear_terms = False

    def create_model(self, n_vars, var_names=None, var_types=None, lb=None, ub=None):
        """Create optimization model with mixed variable types"""
        self.model = pyo.ConcreteModel(self.name)
        self.model.I = pyo.RangeSet(1, n_vars)

        # Handle variable names
        if var_names is None:
            self.var_names = [f"x{i}" for i in range(1, n_vars + 1)]
        else:
            self.var_names = list(var_names[:n_vars])
            while len(self.var_names) < n_vars:
                self.var_names.append(f"x{len(self.var_names) + 1}")

        # Handle variable types
        if var_types is None:
            self.var_types = ['continuous'] * n_vars
        elif isinstance(var_types, str):
            self.var_types = [var_types] * n_vars
        else:
            self.var_types = list(var_types[:n_vars])
            while len(self.var_types) < n_vars:
                self.var_types.append('continuous')

        # Track variable types
        self.has_integer_vars = any(vtype in ['integer', 'binary'] for vtype in self.var_types)
        self.has_continuous_vars = any(vtype == 'continuous' for vtype in self.var_types)

        # Create variables with individual domains
        self.model.x = pyo.Var(self.model.I)

        for i, var_type in enumerate(self.var_types, 1):
            if var_type == 'continuous':
                self.model.x[i].domain = pyo.Reals
            elif var_type == 'integer':
                self.model.x[i].domain = pyo.Integers
            elif var_type == 'binary':
                self.model.x[i].domain = pyo.Binary
            else:
                self.model.x[i].domain = pyo.Reals

        # Set bounds with safety for nonlinear functions
        if lb is not None:
            if isinstance(lb, (int, float)):
                lb = [lb] * n_vars
            for i, lower in enumerate(lb, 1):
                if lower is not None and i <= n_vars:
                    # Safe bounds for sqrt and other nonlinear functions
                    safe_lower = max(lower, 1e-6) if lower >= 0 else lower
                    self.model.x[i].setlb(safe_lower)

        if ub is not None:
            if isinstance(ub, (int, float)):
                ub = [ub] * n_vars
            for i, upper in enumerate(ub, 1):
                if upper is not None and i <= n_vars:
                    self.model.x[i].setub(upper)

        return self

    def set_objective(self, objective_func, sense='minimize'):
        """Set objective function with type detection"""
        if sense.lower() in ['minimize', 'min']:
            self.model.obj = pyo.Objective(expr=objective_func(self.model), sense=pyo.minimize)
        else:
            self.model.obj = pyo.Objective(expr=objective_func(self.model), sense=pyo.maximize)

        self._detect_problem_type()
        return self

    def _detect_problem_type(self):
        """Detect problem type based on objective and variables"""
        self.has_quadratic_terms = False
        self.has_nonlinear_terms = False

        try:
            obj_str = str(self.model.obj.expr).lower()

            # Check for quadratic terms
            import re
            if (re.search(r'x\[\d+\]\*\*2', obj_str) or
                    re.search(r'x\[\d+\]\s*\*\s*x\[\d+\]', obj_str)):
                self.has_quadratic_terms = True

            # Check for nonlinear terms (sqrt, exp, log, higher powers)
            nonlinear_keywords = ['exp', 'log', 'sin', 'cos', 'sqrt']
            higher_powers = [f'**{i}' for i in range(3, 10)] + ['**0.5', '**1.5']

            if (any(keyword in obj_str for keyword in nonlinear_keywords) or
                    any(power in obj_str for power in higher_powers)):
                self.has_nonlinear_terms = True

        except:
            pass

        # Determine problem type
        if self.has_integer_vars and self.has_continuous_vars:
            # Mixed integer problem
            if self.has_nonlinear_terms:
                self.problem_type = "MINLP"
            elif self.has_quadratic_terms:
                self.problem_type = "MIQP"
            else:
                self.problem_type = "MILP"
        elif self.has_integer_vars:
            # Pure integer problem
            if self.has_nonlinear_terms:
                self.problem_type = "INLP"
            elif self.has_quadratic_terms:
                self.problem_type = "IQP"
            else:
                self.problem_type = "ILP"
        else:
            # Pure continuous problem
            if self.has_nonlinear_terms:
                self.problem_type = "NLP"
            elif self.has_quadratic_terms:
                self.problem_type = "QP"
            else:
                self.problem_type = "LP"

    def add_constraint(self, constraint_func, sense='<=', name=None):
        """Add single constraint"""
        self.constraint_counter += 1
        if name is None:
            name = f"constraint_{self.constraint_counter}"

        if sense == '<=':
            expr = constraint_func(self.model) <= 0
        elif sense == '>=':
            expr = constraint_func(self.model) >= 0
        else:  # '='
            expr = constraint_func(self.model) == 0

        setattr(self.model, name, pyo.Constraint(expr=expr))
        return self

    def add_linear_constraints(self, A, b, sense='<='):
        """Add multiple linear constraints"""
        A = np.array(A)
        b = np.array(b)

        if A.ndim == 1:
            A = A.reshape(1, -1)

        self.constraint_counter += 1
        constraint_name = f'linear_constraints_{self.constraint_counter}'

        if sense == '<=':
            def rule(model, i):
                return sum(A[i - 1, j - 1] * model.x[j] for j in model.I) <= b[i - 1]
        elif sense == '>=':
            def rule(model, i):
                return sum(A[i - 1, j - 1] * model.x[j] for j in model.I) >= b[i - 1]
        else:  # '='
            def rule(model, i):
                return sum(A[i - 1, j - 1] * model.x[j] for j in model.I) == b[i - 1]

        setattr(self.model, constraint_name,
                pyo.Constraint(pyo.RangeSet(1, len(b)), rule=rule))

        return self

    def solve(self, solver=None, options=None, verbose=False):
        """Solve optimization problem"""
        if self.model is None:
            print("❌ No model created!")
            return False

        # Auto-select solver
        if solver is None:
            if self.problem_type in ["LP", "QP", "NLP"]:
                solver = "ipopt" if self.problem_type == "NLP" else "gurobi"
            else:
                solver = "gurobi" if pyo.SolverFactory('gurobi').available() else "ipopt"

        if not pyo.SolverFactory(solver).available():
            print(f"❌ Solver {solver} not available!")
            return False

        # Create solver
        self.solver = pyo.SolverFactory(solver)

        # Set solver options
        if solver == 'ipopt':
            clean_options = {
                'print_level': 0,  # Silent IPOPT
                'max_iter': 3000,
                'tol': 1e-6,
                'linear_solver': 'mumps'
            }
            if options:
                clean_options.update(options)

            for key, value in clean_options.items():
                self.solver.options[key] = value
        elif options:
            for key, value in options.items():
                self.solver.options[key] = value

        # Set safe initial point for nonlinear problems
        if self.has_nonlinear_terms:
            try:
                for i in self.model.I:
                    if self.model.x[i].value is None:
                        lb = self.model.x[i].lb if self.model.x[i].lb is not None else 0
                        ub = self.model.x[i].ub if self.model.x[i].ub is not None else 10
                        initial_val = max((lb + ub) / 2, 0.1)
                        self.model.x[i].set_value(initial_val)
            except:
                pass

        # Solve
        try:
            self.results = self.solver.solve(self.model, tee=verbose)

            if (self.results.solver.status == SolverStatus.ok and
                    self.results.solver.termination_condition in [TerminationCondition.optimal,
                                                                  TerminationCondition.locallyOptimal,
                                                                  TerminationCondition.feasible]):
                return True
            else:
                return False

        except:
            return False

    def get_solution(self):
        """Get solution information"""
        if not self.results:
            return None

        try:
            solution = {
                'objective_value': pyo.value(self.model.obj),
                'variables': {},
                'variable_types': {},
                'problem_type': self.problem_type,
                'solver_status': str(self.results.solver.status),
                'termination_condition': str(self.results.solver.termination_condition),
                'has_mixed_variables': self.has_integer_vars and self.has_continuous_vars
            }

            for i in self.model.I:
                var_name = self.var_names[i - 1]
                var_type = self.var_types[i - 1]
                value = pyo.value(self.model.x[i])
                solution['variables'][var_name] = value if value is not None else 0.0
                solution['variable_types'][var_name] = var_type

            return solution
        except:
            return None

    def print_solution(self):
        solution = self.get_solution()
        if not solution:
            print("❌ No solution available")
            return

        print(f"\n📊 {solution['problem_type']} SOLUTION")
        print("=" * 50)
        print(f"Objective Value: {solution['objective_value']:.6f}")

        # Show variable types for mixed problems
        if solution['has_mixed_variables']:
            print("Variable Types:")
            continuous_vars = [name for name, vtype in solution['variable_types'].items()
                               if vtype == 'continuous']
            integer_vars = [name for name, vtype in solution['variable_types'].items()
                            if vtype == 'integer']
            binary_vars = [name for name, vtype in solution['variable_types'].items()
                           if vtype == 'binary']

            if continuous_vars:
                print(f"  Continuous: {', '.join(continuous_vars)}")
            if integer_vars:
                print(f"  Integer: {', '.join(integer_vars)}")
            if binary_vars:
                print(f"  Binary: {', '.join(binary_vars)}")

        print("Variable Values:")
        for name, value in solution['variables'].items():
            var_type = solution['variable_types'][name]
            if var_type in ['integer', 'binary'] and abs(value - round(value)) < 1e-6:
                print(f"  {name} = {int(round(value))} ({var_type})")
            else:
                print(f"  {name} = {value:.6f} ({var_type})")

    def plot_solution_2d(self, x_range=None, y_range=None, title=None, figsize=(10, 7)):
        """Plot 2D solution with ALL ENGLISH LABELS"""
        solution = self.get_solution()
        if not solution or len(solution['variables']) != 2:
            print(
                f"⚠️ Cannot plot: Problem has {len(solution['variables']) if solution else 0} variables (need exactly 2 for 2D plot)")
            return

        if x_range is None:
            x_range = (0, 10)
        if y_range is None:
            y_range = (0, 10)
        if title is None:
            title = f"{self.name}"

        # Get solution point and variable types
        vars_list = list(solution['variables'].items())
        x_opt, y_opt = vars_list[0][1], vars_list[1][1]
        x_name, y_name = vars_list[0][0], vars_list[1][0]
        x_type = solution['variable_types'][x_name]
        y_type = solution['variable_types'][y_name]

        # Create plot with ALL ENGLISH LABELS
        fig, ax = plt.subplots(figsize=figsize)

        # Plot optimal point with markers based on variable types
        if x_type in ['integer', 'binary'] or y_type in ['integer', 'binary']:
            ax.plot(x_opt, y_opt, 'rs', markersize=14, zorder=5,
                    label=f'Optimal Solution\n({x_opt:.3f}, {y_opt:.3f})')
        else:
            ax.plot(x_opt, y_opt, 'ro', markersize=14, zorder=5,
                    label=f'Optimal Solution\n({x_opt:.3f}, {y_opt:.3f})')

        # Annotation with ENGLISH TEXT and variable types
        annotation_text = (f'Optimal Point\n'
                           f'{x_name}: {x_opt:.3f} ({x_type})\n'
                           f'{y_name}: {y_opt:.3f} ({y_type})\n'
                           f'Objective Value: {solution["objective_value"]:.3f}')

        ax.annotate(annotation_text,
                    xy=(x_opt, y_opt),
                    xytext=(x_opt + (x_range[1] - x_range[0]) * 0.15,
                            y_opt + (y_range[1] - y_range[0]) * 0.15),
                    arrowprops=dict(arrowstyle='->', color='red', lw=2),
                    bbox=dict(boxstyle="round,pad=0.5", facecolor="yellow", alpha=0.8),
                    fontsize=12, ha='left')

        # Set ALL ENGLISH AXIS LABELS
        ax.set_xlim(x_range)
        ax.set_ylim(y_range)
        ax.set_xlabel(f'{x_name} ({x_type})', fontsize=14, fontweight='bold')
        ax.set_ylabel(f'{y_name} ({y_type})', fontsize=14, fontweight='bold')
        ax.set_title(f'{title} ({solution["problem_type"]} Problem)',
                     fontsize=16, fontweight='bold')

        ax.grid(True, alpha=0.3)
        ax.legend(fontsize=12, loc='best')

        # Add variable information box in ENGLISH
        if solution['has_mixed_variables']:
            info_text = "Mixed Variable Types:\n"
            for name, vtype in solution['variable_types'].items():
                info_text += f"{name}: {vtype}\n"

            ax.text(0.02, 0.98, info_text.strip(), transform=ax.transAxes,
                    bbox=dict(boxstyle="round,pad=0.3", facecolor="lightblue", alpha=0.7),
                    fontsize=10, verticalalignment='top')

        # ENGLISH TIMESTAMP
        timestamp_text = f"Generated: 2025-06-20 10:58:07 UTC | User: giraffishh"
        fig.text(0.99, 0.01, timestamp_text, ha='right', va='bottom',
                 fontsize=9, alpha=0.6)

        plt.tight_layout()
        plt.show()
        print(f"✅ Plot created for {solution['problem_type']} problem with ALL ENGLISH LABELS")


# Example 1: LP - x,y (continuous, continuous)
def example_linear_programming():
    """Example 1: Linear Programming - All continuous variables"""
    print("🎯Example 1: Linear Programming (LP)")
    print("Variables: x,y (continuous, continuous)")
    print("Maximize: 3x + 2y")
    print("Subject to: x + y ≤ 4, 2x + y ≤ 6, x,y ≥ 0")

    solver = OptimizationSolver("Linear_Programming")
    solver.create_model(n_vars=2, var_names=['x', 'y'],
                        var_types=['continuous', 'continuous'], lb=[0, 0])

    # Linear objective
    def objective(model):
        return 3 * model.x[1] + 2 * model.x[2]

    solver.set_objective(objective, 'maximize')
    solver.add_linear_constraints(A=[[1, 1], [2, 1]], b=[4, 6], sense='<=')

    if solver.solve():
        solver.print_solution()
        solver.plot_solution_2d(x_range=(0, 5), y_range=(0, 5), title="Linear Programming")
        return solver.get_solution()
    return None


# Example 2: MILP - x,y (continuous, integer)
def example_mixed_integer_programming():
    """Example 2: Mixed Integer Linear Programming - Mixed variables"""
    print("\n🎯Example 2: Mixed Integer Linear Programming (MILP)")
    print("Variables: x,y (continuous, integer)")
    print("Minimize: 2x + 3y")
    print("Subject to: x + 2y ≥ 5, x ≥ 0 (continuous), y ∈ Z+ (integer)")

    solver = OptimizationSolver("Mixed_Integer_Programming")
    solver.create_model(n_vars=2, var_names=['x', 'y'],
                        var_types=['continuous', 'integer'], lb=[0, 0])

    # Linear objective with mixed variables
    def objective(model):
        return 2 * model.x[1] + 3 * model.x[2]

    solver.set_objective(objective, 'minimize')
    solver.add_linear_constraints(A=[[1, 2]], b=[5], sense='>=')

    if solver.solve():
        solver.print_solution()
        solver.plot_solution_2d(x_range=(0, 6), y_range=(0, 4), title="Mixed Integer Programming")
        return solver.get_solution()
    return None


# Example 3: NLP - x,y (continuous, continuous) with sqrt and cubic
def example_nonlinear_programming():
    """Example 3: Nonlinear Programming - sqrt and cubic terms"""
    print("\n🎯Example 3: Nonlinear Programming (NLP)")
    print("Variables: x,y (continuous, continuous)")
    print("Minimize: sqrt(x) + y³ + 0.1x + 0.1y")
    print("Subject to: x + y ≥ 2, x ≥ 0.01, y ≥ 0.01")

    solver = OptimizationSolver("Nonlinear_Programming")
    solver.create_model(n_vars=2, var_names=['x', 'y'],
                        var_types=['continuous', 'continuous'],
                        lb=[0.01, 0.01], ub=[10, 10])

    # Nonlinear objective with sqrt(x) and y³
    def objective(model):
        return (pyo.sqrt(model.x[1]) + model.x[2] ** 3 +
                0.1 * model.x[1] + 0.1 * model.x[2])

    solver.set_objective(objective, 'minimize')

    # Linear constraint
    def constraint(model):
        return model.x[1] + model.x[2] - 2

    solver.add_constraint(constraint, '>=')

    if solver.solve():
        solver.print_solution()
        solver.plot_solution_2d(x_range=(0, 5), y_range=(0, 3), title="Nonlinear Programming")
        return solver.get_solution()
    return None


# Example 4: QP - x,y (continuous, continuous)
def example_quadratic_programming():
    """Example 4: Quadratic Programming - Quadratic terms"""
    print("\n🎯Example 4: Quadratic Programming (QP)")
    print("Variables: x,y (continuous, continuous)")
    print("Minimize: x² + y² - 4x - 6y")
    print("Subject to: x + y ≤ 5, x,y ≥ 0")
    solver = OptimizationSolver("Quadratic_Programming")

    # Quadratic objective
    def objective(model):
        return model.x[1] ** 2 + model.x[2] ** 2 - 4 * model.x[1] - 6 * model.x[2]

    # Support chain calls
    solver.create_model(n_vars=2, var_names=['x', 'y'],
                        var_types=['continuous', 'continuous'], lb=[0, 0]) \
        .set_objective(objective, 'minimize') \
        .add_linear_constraints(A=[[1, 1]], b=[5], sense='<=')

    if solver.solve():
        solver.print_solution()
        solver.plot_solution_2d(x_range=(0, 6), y_range=(0, 6), title="Quadratic Programming")
        return solver.get_solution()
    return None


def main():
    """Main function with updated examples"""

    # Run 4 updated examples
    results = []

    try:
        results.append(example_linear_programming())  # LP - x,y (continuous, continuous)
        results.append(example_mixed_integer_programming())  # MILP - x,y (continuous, integer)
        results.append(example_nonlinear_programming())  # NLP - x,y (continuous, continuous) with sqrt and cubic
        results.append(example_quadratic_programming())  # QP - x,y (continuous, continuous)

    except Exception as e:
        print(f"❌ Error: {e}")

    # Summary with ALL ENGLISH labels
    print(f"\n📊 SUMMARY")
    print("=" * 70)

    examples = [
        ("Linear Programming", "LP", "x,y (continuous, continuous)"),
        ("Mixed Integer Linear Programming", "MILP", "x,y (continuous, integer)"),
        ("Nonlinear Programming", "NLP", "x,y (continuous, continuous) - sqrt & cubic"),
        ("Quadratic Programming", "QP", "x,y (continuous, continuous)")
    ]

    successful = sum(1 for r in results if r is not None)

    for i, (name, expected_type, description) in enumerate(examples):
        if i < len(results) and results[i] is not None:
            actual_type = results[i]['problem_type']
            has_mixed = results[i].get('has_mixed_variables', False)
            mixed_info = " (Mixed Variables)" if has_mixed else ""
            print(f"✅ {name}: {actual_type}{mixed_info} - {description}")
        else:
            print(f"❌ {name}: Failed")

    print(f"\nSolved: {successful}/4 problems")

if __name__ == "__main__":
    main()

说明:

方法	功能	示例
`create_model(n_vars, var_names, var_types, lb, ub)`	创建模型	`solver.create_model(2, ['x','y'], 'continuous', lb=[0,0])`
`set_objective(objective_func, sense)`	设置目标函数	`solver.set_objective(obj_func, 'maximize')`
`add_linear_constraints(A, b, sense)`	添加线性约束	`solver.add_linear_constraints([[1,1]], [5], '<=')`
`add_constraint(constraint_func, sense)`	添加单个约束	`solver.add_constraint(constraint, '>=')`
`solve(solver, options, verbose)`	求解问题	`solver.solve()`
`print_solution()`	打印解	`solver.print_solution()`
`plot_solution_2d()`	2D图表	`solver.plot_solution_2d()`

支持方法链式调用

solver.create_model(2, ['x','y'], lb=[0,0]) \
      .set_objective(obj_func, 'maximize') \
      .add_linear_constraints(A, b, '<=') \
      .solve()

注意：在构造符号表达式应使用Pyomo中的方法而不是Python的math库

# 示例
import pyomo.environ as pyo

pyo.sqrt(model.x[1])

exp(x)：指数函数 $e^x$
log(x)：自然对数 $\ln(x)$ （要求 $x > 0$ ）
log10(x)：以 10 为底的对数 $\log_{10}(x)$
sqrt(x)：平方根 $\sqrt{x}$
x ** n：幂函数（支持变量或表达式的幂）
sin(x)：正弦函数
cos(x)：余弦函数
tan(x)：正切函数
asin(x)：反正弦（值域为 [-π/2, π/2]）
acos(x)：反余弦（值域为 [0, π]）
atan(x)：反正切（值域为 [-π/2, π/2]）
sinh(x)：双曲正弦
cosh(x)：双曲余弦
tanh(x)：双曲正切
abs(x)：绝对值（自动引入约束）
ceil(x)：向上取整（整数规划中慎用）
floor(x)：向下取整（同上）
max_(x, y)：最大值（注意末尾是下划线，避免与 Python 保留字冲突）
min_(x, y)：最小值

注意某些函数（如 log、sqrt）在边界点（如 0）求导会出错，应设置合理的变量下限

层析分析法（AHP）

“层次分析法”（Analytic Hierarchy Process，简称 AHP）是一种多准则决策分析方法，由美国运筹学家托马斯·萨蒂（Thomas L. Saaty）在20世纪70年代提出的。它用于将复杂的决策问题分解成多个层次结构，并通过成对比较和一致性检验来确定各因素的相对重要性

层次分析法的三大典型应用

用于最佳方案的选取（选择地址）
用于评价类问题（评价水质状况、评价环境）
用于指标体系的优选（兼顾科学和效率）

核心步骤

建立层次结构模型
将问题抽象成目标、准则和方案三个层次，形成树状结构。
构造判断矩阵
采用成对比较的方法，专家对每一层因素进行两两比较，使用 1~9 标度法填写判断矩阵。例如，“因素 A 比因素 B 重要”可用数值表示。
计算权重向量
求解判断矩阵的特征向量，得到每个因素的相对权重（即重要性）。
一致性检验
判断专家打分是否逻辑一致。如果不一致（CI 值超过阈值），需要重新打分。
综合权重计算
逐层计算出最终每个方案的综合得分，选择得分最高的方案。

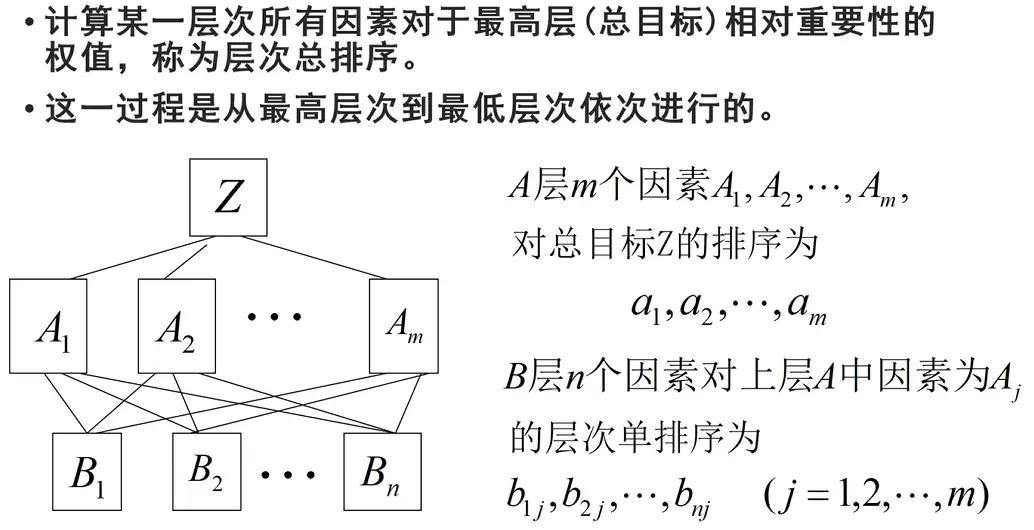
1. 建立层次结构模型

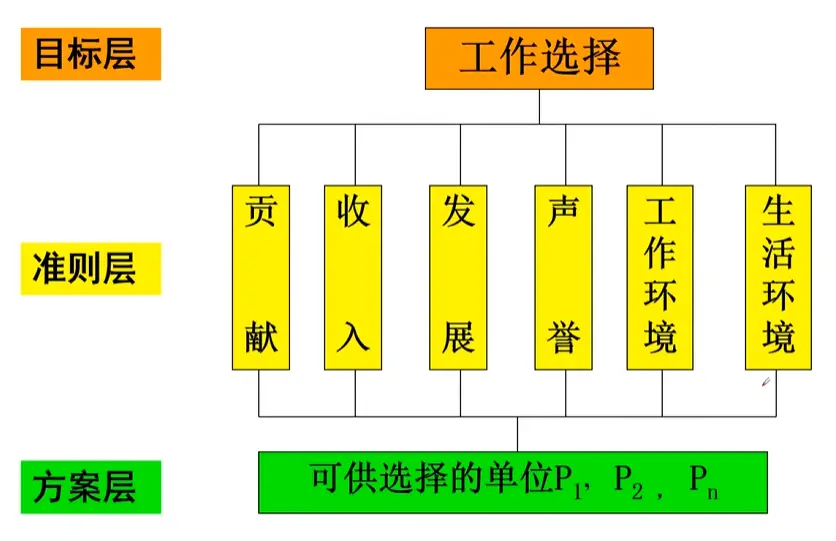
AHP 通过将复杂问题结构化，分成三个主要层次：

目标层（目标）：决策的最终目标，比如“选出最优方案”
准则层（或叫标准层）：影响目标实现的准则或指标
方案层：备选的决策方案

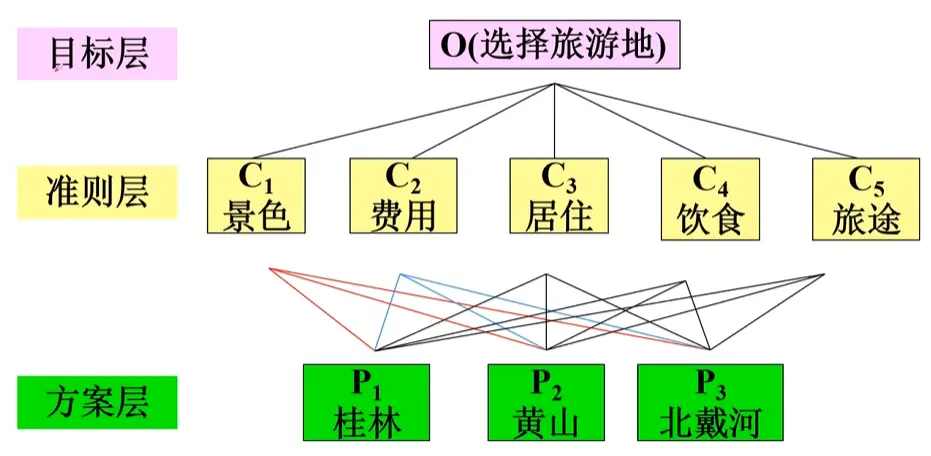
示例:

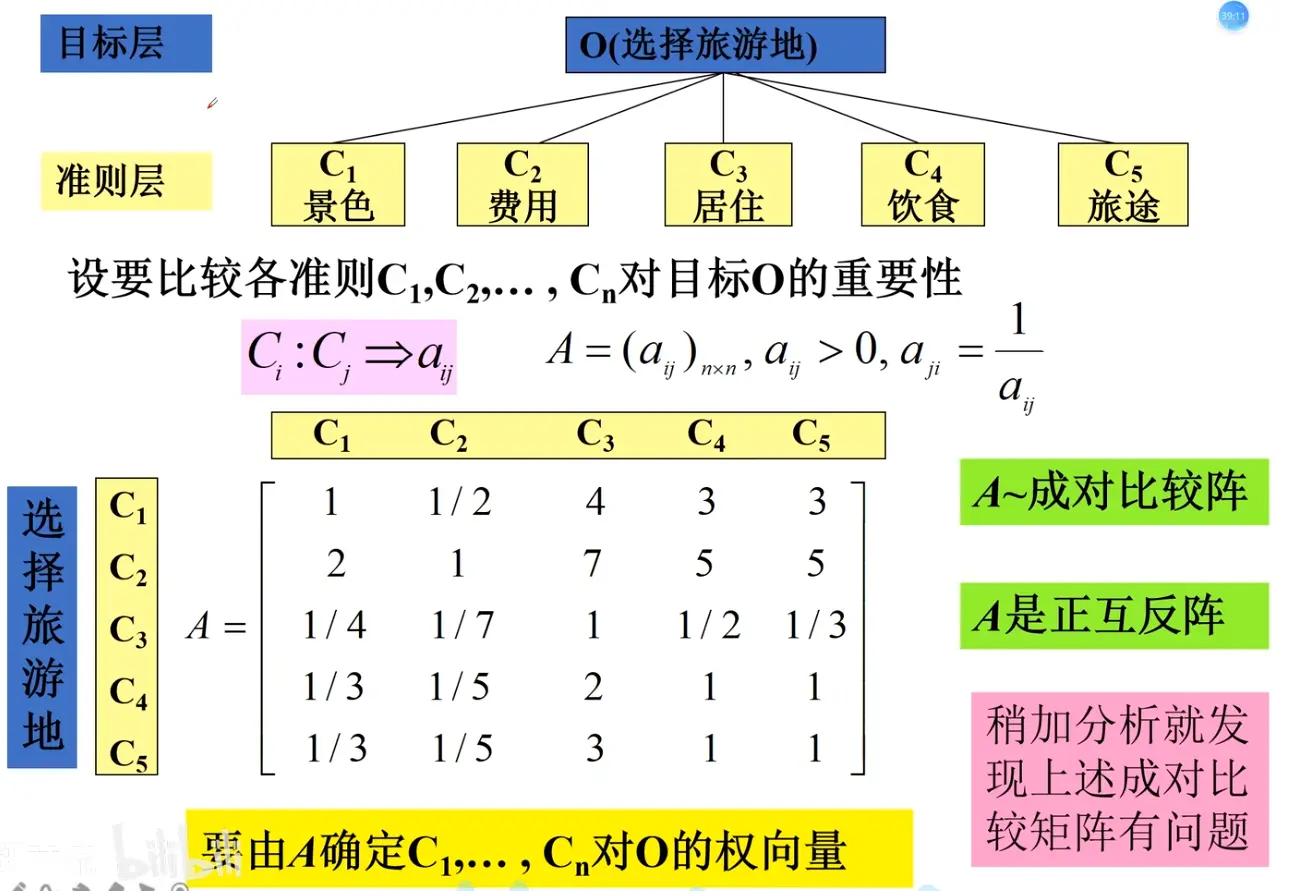
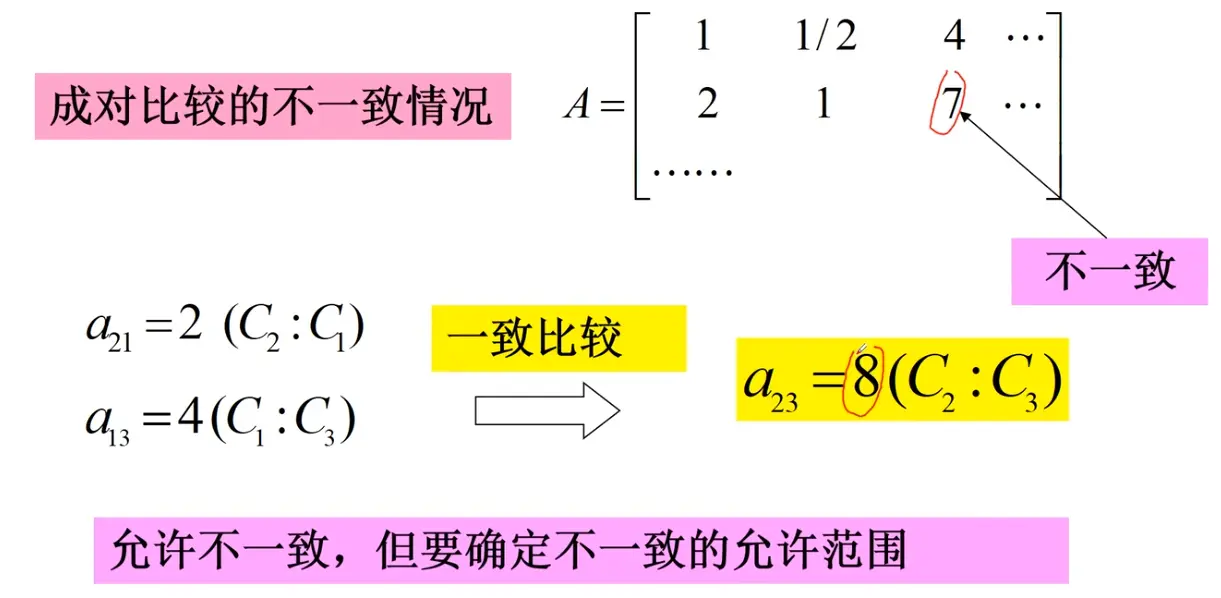
2. 构造判断（成对比较）矩阵

在确定各层次各因素之间的权重时，如果只是定性的结果，常常不容易被他人接受。因此，Saaty 等人提出“一致矩阵法”，其主要思想包括：

不把所有因素放在一起比较，而是两两相互比较；
采用相对尺度，尽可能减少性质不同的因素直接比较的困难，以提高判断的准确度。

判断矩阵用于表示本层所有因素针对上一层某一个因素的相对重要性。判断矩阵中的元素 $a_{ij}$ 由 Saaty 提出的 1—9 标度法给出，用来量化“因素 $i$ 相对于因素 $j$ 的重要性”

心理学研究表明，成对比较的因素不宜超过 9 个，因此每一层的因素数量通常控制在 9 个以内

判断矩阵元素 $a_{ij}$ 的标度方法

标度	含义
1	表示两个因素相比，具有同样重要性
3	表示两个因素相比，一个因素比另一个因素稍微重要
5	表示两个因素相比，一个因素比另一个因素明显重要
7	表示两个因素相比，一个因素比另一个因素强烈重要
9	表示两个因素相比，一个因素比另一个因素极端重要
2, 4, 6, 8	上述两相邻判断的中值
倒数	因素 $i$ 与 $j$ 比较的判断 $a_{ij}$ ，则因素 $j$ 与 $i$ 比较的判断 $a_{ji} = 1/a_{ij}$

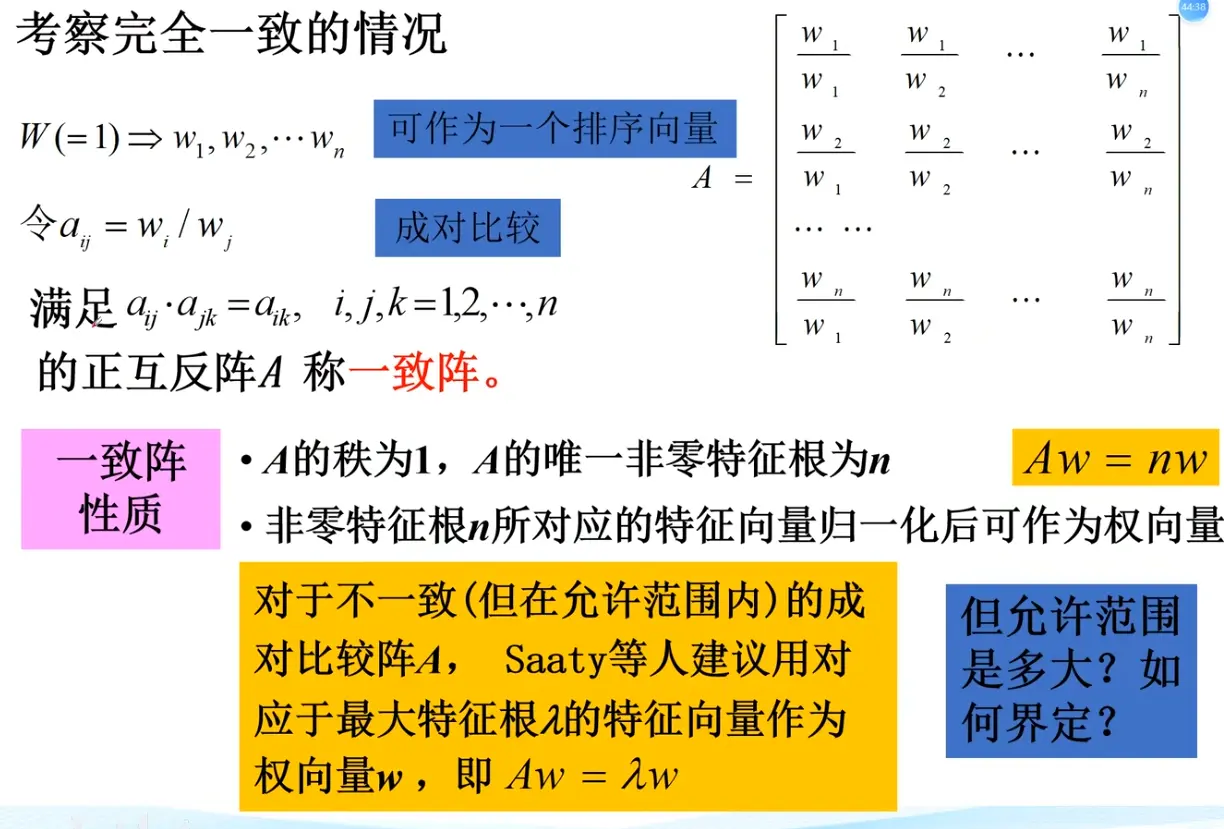
3. 计算权重向量

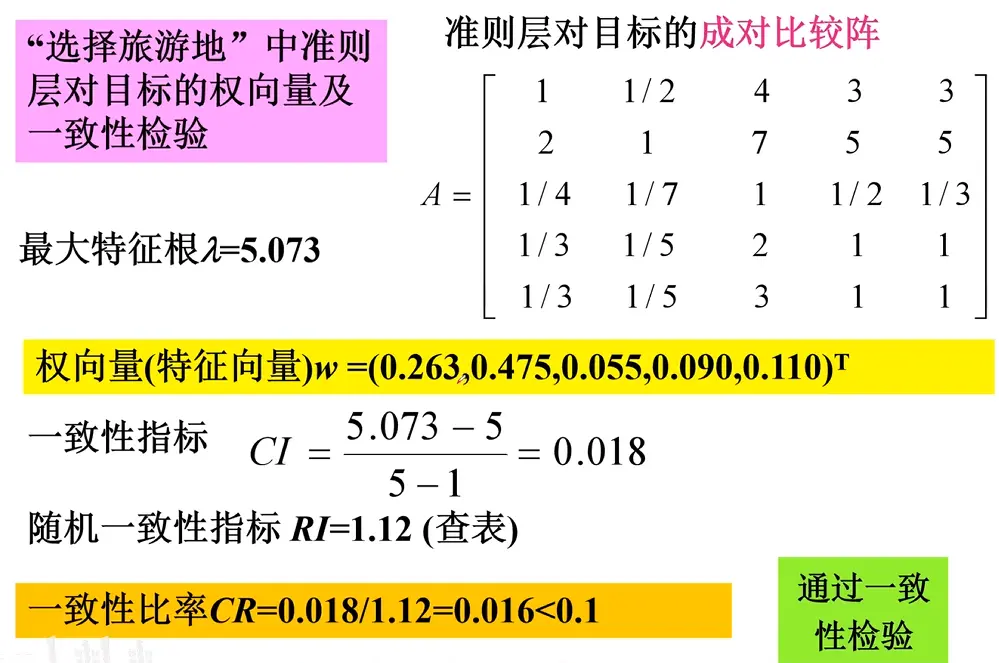
4. 一致性检验

5. 综合权重计算

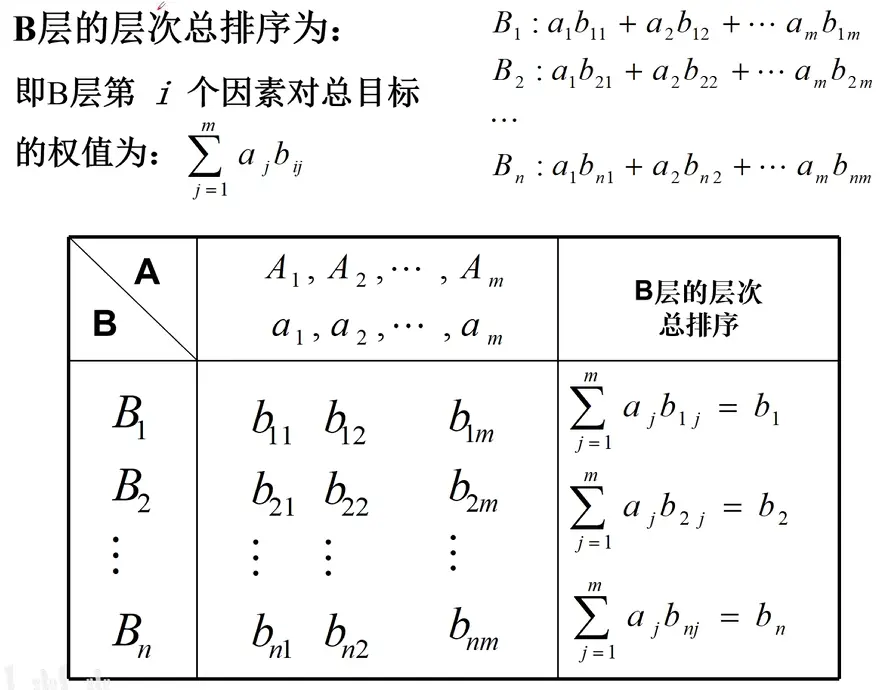
上述步骤2-4完成了准则层到目标层的权重向量（层次单排序），现在需要重复2-4的步骤，完成方案层对每一个准则层的权重向量，即方案在每一个评判准则上的“得分”， $\sum (\text{得分} \times \text{权重}) = \text{总得分}$ ，即层次总排序

层次总排序的一致性检验

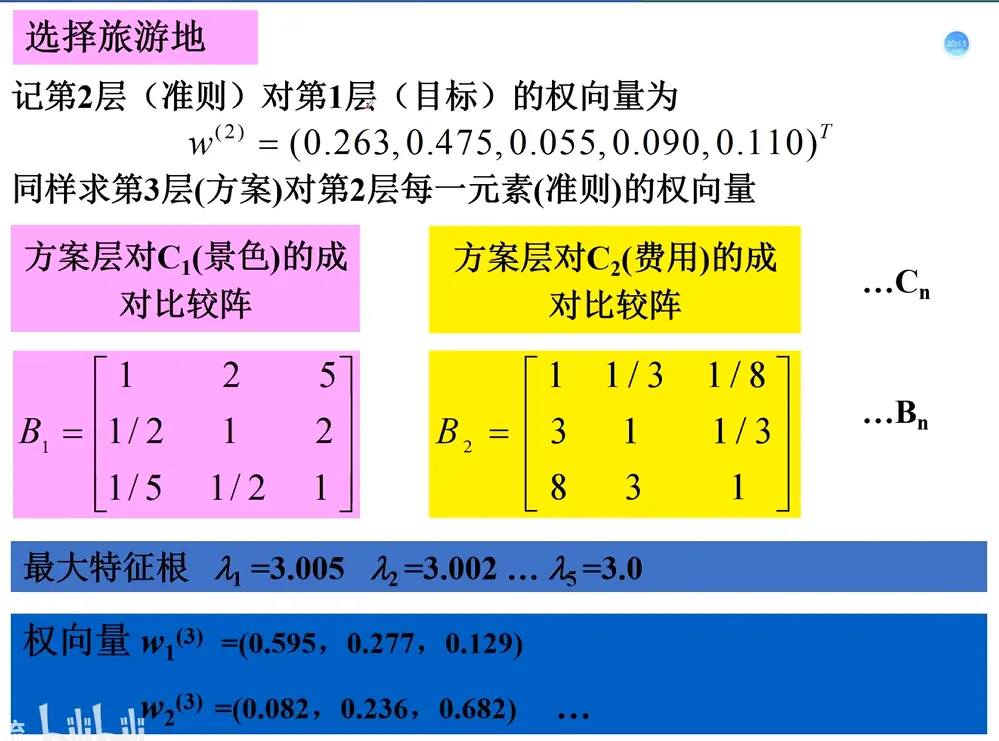
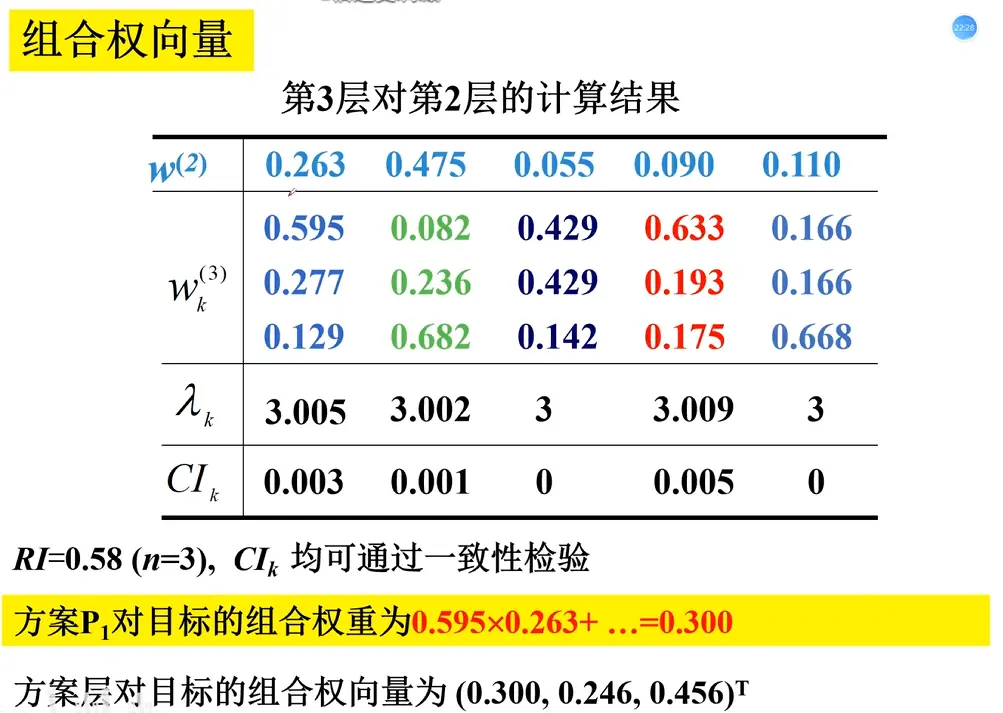
示例

示例代码

import numpy as np
from scipy.linalg import eig


class AHP:
    """
    A class to implement the Analytic Hierarchy Process.
    """

    def __init__(self, criteria_matrix, alternatives_matrices):
        """
        Initialize the AHP model.
        :param criteria_matrix: The pairwise comparison matrix for the criteria.
        :param alternatives_matrices: A list of pairwise comparison matrices for the alternatives,
                                      one for each criterion.
        """
        self.criteria_matrix = np.array(criteria_matrix, dtype=float)
        self.alternatives_matrices = [np.array(m, dtype=float) for m in alternatives_matrices]

        self.num_criteria = self.criteria_matrix.shape[0]
        self.num_alternatives = self.alternatives_matrices[0].shape[0]

        # Predefined Random Index (RI) for matrices of size 1 to 10
        # Saaty's 1980 RI values
        self.RI = {
            1: 0, 2: 0, 3: 0.58, 4: 0.90, 5: 1.12,
            6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45, 10: 1.49
        }

    def _calculate_weights(self, matrix):
        """
        Calculate the priority vector (weights) from a pairwise comparison matrix.
        This uses the principal eigenvalue method.
        """
        # Calculate eigenvalues and eigenvectors
        eigenvalues, eigenvectors = eig(matrix)

        # Find the index of the largest real eigenvalue
        max_eigenvalue_index = np.argmax(np.real(eigenvalues))

        # Get the corresponding eigenvector
        principal_eigenvector = np.real(eigenvectors[:, max_eigenvalue_index])

        # Normalize the eigenvector to get weights (ensure positive values)
        if np.sum(principal_eigenvector) < 0:
            principal_eigenvector = -principal_eigenvector

        weights = principal_eigenvector / np.sum(principal_eigenvector)

        return weights

    def _check_consistency(self, matrix):
        """
        Check the consistency of a pairwise comparison matrix.
        Returns the Consistency Ratio (CR). A CR of 0.10 or less is considered acceptable.
        """
        n = matrix.shape[0]
        if n <= 2:
            return 0.0  # Matrices of size 1 or 2 are always consistent

        weights = self._calculate_weights(matrix)

        # Calculate lambda_max
        weighted_sum_vector = np.dot(matrix, weights)
        lambda_max = np.mean(weighted_sum_vector / weights)

        # Calculate Consistency Index (CI)
        CI = (lambda_max - n) / (n - 1)

        # Get Random Index (RI)
        RI = self.RI.get(n)
        if RI is None or RI == 0:
            return float('inf')  # Should not happen for n > 2 with the given RI table

        # Calculate Consistency Ratio (CR)
        CR = CI / RI
        return CR

    def calculate_final_scores(self):
        """
        Calculate the final scores for each alternative.
        """
        # 1. Calculate criteria weights and check consistency
        criteria_weights = self._calculate_weights(self.criteria_matrix)
        criteria_cr = self._check_consistency(self.criteria_matrix)

        print("--- Criteria Analysis ---")
        print(f"Criteria Weights: {np.round(criteria_weights, 4)}")
        print(f"Criteria Consistency Ratio (CR): {criteria_cr:.4f}")
        if criteria_cr > 0.1:
            print("Warning: The criteria comparison matrix is inconsistent (CR > 0.1).")
        print("-" * 25)

        # 2. Calculate alternative weights for each criterion
        alternative_weights_matrix = []
        for i, alt_matrix in enumerate(self.alternatives_matrices):
            alt_weights = self._calculate_weights(alt_matrix)
            alt_cr = self._check_consistency(alt_matrix)
            alternative_weights_matrix.append(alt_weights)

            print(f"\n--- Analysis for Criterion {i + 1} ---")
            print(f"Alternative Weights: {np.round(alt_weights, 4)}")
            print(f"Consistency Ratio (CR): {alt_cr:.4f}")
            if alt_cr > 0.1:
                print(f"Warning: The alternative comparison matrix for criterion {i + 1} is inconsistent (CR > 0.1).")
            print("-" * 25)

        # 3. Synthesize the results to get final scores
        alternative_weights_matrix = np.array(alternative_weights_matrix).T
        final_scores = np.dot(alternative_weights_matrix, criteria_weights)

        return final_scores

if __name__ == '__main__':
    # --- Step 1: Define your problem ---
    # Goal: Choose the best car

    criteria_labels = ["Price", "Safety", "Performance"]
    alternatives_labels = ["Car A", "Car B", "Car C"]

    # --- Step 2: Create pairwise comparison matrices ---
    # These matrices represent subjective judgments.
    # The scale typically ranges from 1 (equal importance) to 9 (extreme importance).
    # If criterion A is '3' times more important than B, then B is '1/3' as important as A.

    # 2.1. Pairwise comparison matrix for the criteria
    #       Price   Safety  Performance
    # Price   1        3         5
    # Safety 1/3       1         2
    # Perf.  1/5      1/2        1
    criteria_matrix = [
        [1, 3, 5],
        [1 / 3, 1, 2],
        [1 / 5, 1 / 2, 1]
    ]

    # 2.2. Pairwise comparison matrices for alternatives for each criterion
    # For "Price" (lower is better, so a cheaper car gets a higher score)
    #       Car A   Car B   Car C
    # Car A   1        5       2
    # Car B  1/5       1      1/3
    # Car C  1/2       3       1
    alternatives_price = [
        [1, 5, 2],
        [1 / 5, 1, 1 / 3],
        [1 / 2, 3, 1]
    ]

    # For "Safety"
    #       Car A   Car B   Car C
    # Car A   1      1/5     1/2
    # Car B   5       1       3
    # Car C   2      1/3      1
    alternatives_safety = [
        [1, 1 / 5, 1 / 2],
        [5, 1, 3],
        [2, 1 / 3, 1]
    ]

    # For "Performance"
    #       Car A   Car B   Car C
    # Car A   1      1/3     1/7
    # Car B   3       1      1/3
    # Car C   7       3       1
    alternatives_performance = [
        [1, 1 / 3, 1 / 7],
        [3, 1, 1 / 3],
        [7, 3, 1]
    ]

    alternatives_matrices = [alternatives_price, alternatives_safety, alternatives_performance]

    # --- Step 3: Run the AHP calculation ---
    ahp_model = AHP(criteria_matrix, alternatives_matrices)
    final_scores = ahp_model.calculate_final_scores()

    # --- Step 4: Display the final results ---
    print("\n\n--- Final Results ---")
    for i, score in enumerate(final_scores):
        print(f"Final Score for {alternatives_labels[i]}: {score:.4f}")

    best_alternative_index = np.argmax(final_scores)
    print(f"\nBased on the AHP model, the best choice is: {alternatives_labels[best_alternative_index]}")

TOPSIS + 熵权法

TOPSIS（Technique for Order Preference by Similarity to Ideal Solution，优劣解距离法）是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距

TOPSIS法引入了两个基本概念：
理想解：设想的最优的解（方案），它的各个属性值都达到各备选方案中的最好的值
负理想解：设想的最劣的解（方案），它的各个属性值都达到各备选方案中的最坏的值

方案排序的规则是把各备选方案与理想解和负理想解做比较，若其中有一个方案最接近理想解，而同时又远离负理想解，则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择

熵权法是一种客观赋权方法，基于信息熵理论确定各评价指标的权重，可用于多种多指标综合评价方法中的权重计算，其核心思想为：

指标值差异越大，包含的信息越多，权重应越大
指标值越接近，说明信息越少，权重应越小

核心步骤

1. 构建决策矩阵

构建决策矩阵 $X = [x_{ij}]$ ，其中 $x_{ij}$ 表示第 $i$ 个方案在第 $j$ 个指标上的数值， $i=1,2,\dots,m$ ， $j=1,2,\dots,n$

2. 标准化决策矩阵

指标类型	指标特点	例子
极大型（效益型）指标	越大（多）越好	颜值、成绩、GDP增速
极小型（成本型）指标	越小（少）越好	脾气、费用、环品率、污染程度
中间型指标	越接近某个值越好	身高、水质量评估时的PH值
区间型指标	落在某个区间最好	体重、体温

将原始矩阵正向化
将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标

指标名称	公式	说明
极大型（效益型）指标	/	/
极小型（成本型）指标	$\hat{x} = \max - x$	$\hat{x}$ 为转化后指标， $\max$ 为指标最大值， $x$ 为原始指标值
中间型指标	$\hat{x}_i = 1 - \frac{	x_i - x_{\text{best}}
区间型指标	$\hat{x}_i = \begin{cases} 1 - \frac{a - x_i}{M}, & x_i < a \\ 1, & a \le x_i \le b \\ 1 - \frac{x_i - b}{M}, & x_i > b \end{cases}$ $M = \max\{a - \min\{x_i\}, \max\{x_i\} - b\}$	$\{x_i\}$ 是一组区间型序列，最优区间为 $[a, b]$

正向矩阵标准化
标准化的方法有很多种，其主要目的就是去除量纲的影响，保证不同评价指标在同一数量级，且数据大小排序不变

假设有 $n$ 个要评价的对象， $m$ 个评价指标（已正向化）构成的正向化矩阵如下：

X = \begin{bmatrix} x_{11} & \cdots & x_{1m} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{nm} \end{bmatrix}

那么，对其标准化的矩阵记为 $Z$ ， $Z$ 中的每一个元素：

Z_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^n x_{ij}^2}}

即：每一个元素除以其所在列的元素的平方和的平方根

3. 熵权法加权标准化矩阵

计算概率矩阵

p_{ij} = \frac{x_{ij}}{\sum_{i=1}^m x_{ij}}

计算信息熵

e_j = -\frac{1}{\ln n} \sum_{i=1}^n p_{ij} \ln p_{ij}

注意：当 $p_{ij} = 0$ 时，定义 $p_{ij} \ln p_{ij} = 0$

计算信息效用值

d_j = 1 - e_j

计算指标权重：

w_j = \frac{d_j}{\sum_{j=1}^m d_j}

利用权重加权

对于标准化矩阵 $Z = [z_{ij}]$ ，每列是归一化的值，每列的权重为 $w_j$ ，则加权后的矩阵 $V = [v_{ij}]$ 中的每一个元素为：

v_{ij} = w_j \cdot z_{ij}

4. 确定正理想解与负理想解

正理想解（最优）： $Z^+ = \{v_1^+, v_2^+, \dots, v_n^+\}$
负理想解（最劣）： $Z^- = \{v_1^-, v_2^-, \dots, v_n^-\}$

对于每个指标 $j$ ：

v_j^+ = \max_i v_{ij}, \quad v_j^- = \min_i v_{ij}

5. 计算各方案到理想解的距离

到正理想解的距离：

D_i^+ = \sqrt{\sum_{j=1}^m (v_{ij} - Z_j^+)^2}

到负理想解的距离：

D_i^- = \sqrt{\sum_{j=1}^m (v_{ij} - Z_j^-)^2}

6. 计算贴近度（最终得分）

S_i = \frac{D_i^+}{D_i^+ + D_i^-}

其中 $0 \le S_i \le 1$ ， $S_i$ 越大表示方案越优

另外我们可以将得分归一化并换成百分制

\tilde{S_i} = \frac{S_i}{\sum_{i=1}^{n} S_i} \times 100

示例

明星Kun在选npy，构建决策矩阵

候选人	颜值	脾气（争吵次数）	身高	体重
A	9	10	175	120
B	8	7	164	80
C	6	3	157	90

其中颜值为极大型指标，脾气极小型指标，身高中间型指标(165)，体重区间型指标（90-100）

正向化

候选人	颜值	脾气（争吵次数）	身高	体重
A	9	0	0	0
B	8	3	0.9	0.5
C	6	7	0.2	1

标准化

候选人	颜值	脾气（争吵次数）	身高	体重
A	0.669	0.000	0.000	0.000
B	0.595	0.394	0.976	0.447
C	0.446	0.919	0.217	0.894

熵权法计算权重

颜值	脾气（争吵次数）	身高	体重
0.008	0.307	0.393	0.291

加权后矩阵

候选人	颜值	脾气	身高	体重
A	0.0057	0.0000	0.0000	0.0000
B	0.0051	0.1210	0.3839	0.1301
C	0.0038	0.2823	0.0853	0.2603

确定正理想解与负理想解：

属性	Z+ (最大)	Z- (最小)
颜值	0.0057	0.0038
脾气	0.2823	0.0000
身高	0.3839	0.0000
体重	0.2603	0.0000

正理想解 Z+: [0.0057, 0.2823, 0.3839, 0.2603]
负理想解 Z-: [0.0038, 0.0000, 0.0000, 0.0000]

计算各方案到理想解的距离

候选人	D+	D-
A	0.5430	0.0019
B	0.2073	0.4230
C	0.2986	0.3934

计算贴近度（最终得分）

候选人	得分
A	0.0035
B	0.6711
C	0.5685

归一化换成百分制

候选人	得分
B	53.99%
C	45.73%
A	0.28%

示例代码

import numpy as np
import matplotlib.pyplot as plt

def topsis(decision_matrix, weights, criteria_specs, alternatives_labels):
    """
    Advanced TOPSIS method that handles multiple criteria types and prints intermediate steps.

    Args:
        decision_matrix (np.ndarray): A 2D numpy array of the decision matrix.
                                      Rows are alternatives, columns are criteria.
        weights (np.ndarray): A 1D numpy array of weights for each criterion.
        criteria_specs (list): A list of tuples specifying the type and parameters for each criterion.
        alternatives_labels (list): A list of strings for labeling the alternatives.

    Returns:
        tuple: A tuple containing:
            - np.ndarray: The closeness coefficient (Si) for each alternative.
            - np.ndarray: The rank of each alternative.
    """
    # Step 1: Forwardization (Convert all criteria to benefit type)
    positive_matrix = np.zeros_like(decision_matrix, dtype=float)

    for i, spec in enumerate(criteria_specs):
        col = decision_matrix[:, i]
        criterion_type = spec[0]

        if criterion_type == 'benefit':
            positive_matrix[:, i] = col
        elif criterion_type == 'cost':
            positive_matrix[:, i] = np.max(col) - col
        elif criterion_type == 'mid':
            best_value = spec[1]
            m = np.max(np.abs(col - best_value))
            if m == 0:
                positive_matrix[:, i] = 1.0
            else:
                positive_matrix[:, i] = 1 - (np.abs(col - best_value) / m)
        elif criterion_type == 'interval':
            lower_bound, upper_bound = spec[1], spec[2]
            m = np.max([lower_bound - np.min(col), np.max(col) - upper_bound])
            transformed_col = np.zeros_like(col, dtype=float)
            if m == 0:
                 for j, val in enumerate(col):
                    if lower_bound <= val <= upper_bound:
                        transformed_col[j] = 1
                    else:
                        transformed_col[j] = 0
            else:
                for j, val in enumerate(col):
                    if val < lower_bound:
                        transformed_col[j] = 1 - (lower_bound - val) / m
                    elif val > upper_bound:
                        transformed_col[j] = 1 - (val - upper_bound) / m
                    else:
                        transformed_col[j] = 1
            positive_matrix[:, i] = transformed_col
        else:
            raise ValueError(f"Unknown criterion type: {criterion_type}")

    # Step 2: Normalize the positive decision matrix
    norm_matrix = positive_matrix / np.sqrt(np.sum(positive_matrix ** 2, axis=0))

    # Step 3: Calculate weights using Entropy Weight Method if not provided
    if weights is None:
        # Calculate probability matrix
        prob_matrix = norm_matrix / np.sum(norm_matrix, axis=0, keepdims=True)

        # Calculate entropy for each criterion
        entropy = np.zeros(prob_matrix.shape[1])
        for j in range(prob_matrix.shape[1]):
            for i in range(prob_matrix.shape[0]):
                if prob_matrix[i, j] == 0:
                    continue
                entropy[j] += prob_matrix[i, j] * np.log(prob_matrix[i, j])
        entropy = -entropy / np.log(norm_matrix.shape[0])

        # Calculate redundancy (utility) for each criterion
        redundancy = 1 - entropy

        # Calculate weights for each criterion
        weights = redundancy / np.sum(redundancy)

    # Step 4: Create the weighted normalized decision matrix
    weighted_matrix = norm_matrix * weights

    print("--- Intermediate Steps ---")
    print("\nStep 1: Forwardized Matrix (Positive Matrix):\n", positive_matrix)
    print("\nStep 2: Normalized Matrix:\n", norm_matrix)
    print("\nStep 3: Calculated Weights (or provided weights):\n", weights)
    print("\nStep 4: Weighted Normalized Matrix:\n", weighted_matrix)
    print("\n" + "=" * 50 + "\n")

    # Step 5: Determine the ideal and negative-ideal solutions
    ideal_solution = np.max(weighted_matrix, axis=0)  # Z+
    negative_ideal_solution = np.min(weighted_matrix, axis=0)  # Z-

    print("--- Ideal and Negative-Ideal Solutions ---")
    print("\nIdeal Solution (Z+):\n", ideal_solution)
    print("\nNegative-Ideal Solution (Z-):\n", negative_ideal_solution)
    print("Ideal Solution (Z+):")
    print(ideal_solution)
    print("\nNegative-Ideal Solution (Z-):")
    print(negative_ideal_solution)
    print("\n" + "="*50 + "\n")


    print("--- Intermediate Step 5: Distances to Ideal Solutions ---")
    # Step 5: Calculate the separation measures
    distance_to_ideal = np.sqrt(np.sum((weighted_matrix - ideal_solution)**2, axis=1))
    distance_to_negative_ideal = np.sqrt(np.sum((weighted_matrix - negative_ideal_solution)**2, axis=1))
    for i, label in enumerate(alternatives_labels):
        print(f"{label} -> Distance to Ideal (D+): {distance_to_ideal[i]:.4f}, Distance to Negative-Ideal (D-): {distance_to_negative_ideal[i]:.4f}")
    print("\n" + "="*50 + "\n")

    # Step 6: Calculate the relative closeness to the ideal solution
    epsilon = 1e-6
    closeness_coefficient = distance_to_negative_ideal / (distance_to_ideal + distance_to_negative_ideal + epsilon)

    # Step 7: Rank the alternatives
    rank = len(closeness_coefficient) - np.argsort(np.argsort(closeness_coefficient))

    return closeness_coefficient, rank

if __name__ == '__main__':
    # --- Example Usage: Candidate Selection ---

    # Alternatives: Candidate A, Candidate B, Candidate C
    alternatives = [f'Candidate {chr(65+i)}' for i in range(3)]

    # Criteria:
    # 1. Appearance (Score) - 'benefit' type
    # 2. Temper (Number of quarrels) - 'cost' type
    # 3. Height (cm) - 'mid' type (best is 165cm)
    # 4. Weight (kg) - 'interval' type (best is between 90-100kg)
    decision_matrix = np.array([
    # Appearance, Temper, Height, Weight
        [9, 10, 175, 120],  # Candidate A
        [8,  7, 164,  80],  # Candidate B
        [6,  3, 157,  90],  # Candidate C
    ])

    # Weights for each criterion. Assuming equal importance.
    weights = None # Use None to calculate weights using entropy method

    # Specifications for each criterion
    criteria_specs = [
        ('benefit',),
        ('cost',),
        ('mid', 165),
        ('interval', 90, 100)
    ]

    # --- Run TOPSIS ---
    closeness_coefficient, rank = topsis(decision_matrix, weights, criteria_specs, alternatives)

    # --- Final Results ---
    print("--- Final Results ---")
    print(f"{'Alternative':<12} | {'Closeness (Si)':<15} | {'Rank':<5}")
    print("-" * 40)
    results_to_display = sorted(zip(alternatives, closeness_coefficient, rank), key=lambda x: x[2])
    for alt, closeness, r in results_to_display:
        print(f"{alt:<12} | {closeness:<15.4f} | {r:<5}")

    # Calculate percentage score
    percentage_score = (closeness_coefficient / np.sum(closeness_coefficient)) * 100
    print("\n--- Final Percentage Scores (Normalized) ---")
    print(f"{'Alternative':<12} | {'Percentage Score':<20}")
    print("-" * 40)
    results_to_display_percent = sorted(zip(alternatives, percentage_score, rank), key=lambda x: x[2])
    for alt, percent_score, r in results_to_display_percent:
        print(f"{alt:<12} | {percent_score:<20.2f}%")

    best_alternative_index = np.argmax(closeness_coefficient)
    print(f"\nBest Alternative based on TOPSIS: {alternatives[best_alternative_index]}")

    # --- Visualize the Results ---
    plt.figure(figsize=(10, 6))
    sorted_indices = np.argsort(rank)
    sorted_alternatives = [alternatives[i] for i in sorted_indices]
    sorted_closeness = closeness_coefficient[sorted_indices]

    bars = plt.bar(sorted_alternatives, sorted_closeness, color='teal')
    plt.xlabel('Alternatives (Sorted by Rank)')
    plt.ylabel('Closeness Coefficient (Si)')
    plt.title('TOPSIS Results: Closeness Coefficient of Candidates')
    plt.ylim(0, max(closeness_coefficient) * 1.2)

    for bar in bars:
        yval = bar.get_height()
        plt.text(bar.get_x() + bar.get_width()/2.0, yval, f'{yval:.4f}', va='bottom', ha='center')

    plt.tight_layout()
    plt.show()

灰色关联分析

灰色关联分析是一种多因素统计分析方法，隶属于灰色系统理论。它通过分析和比较数据序列的几何形状相似度，来判断不同序列之间的关联程度。当两个序列的曲线变化趋势越一致，它们的关联度就越高，反之则越低

该方法尤其适用于样本量小、信息不完全的系统，以及因素之间关系不明确的情况。与传统的回归分析等方法相比，灰色关联分析对数据分布没有严格要求，计算简便，结果直观易懂

灰色系统

灰色系统理论是一种研究和解决信息不完全、数据量小问题的有效方法。它把所有信息都已知的系统看作“白色”（如实验室环境），把信息完全未知的系统看作“黑色”（如黑箱），而把介于两者之间、信息部分明确、部分不明确的系统，就称为“灰色系统”

灰色系统理论主要包括以下几个分支：

灰色关联分析
灰色预测
灰色决策
灰色聚类

核心步骤

1. 确定分析序列（母序列和子序列）

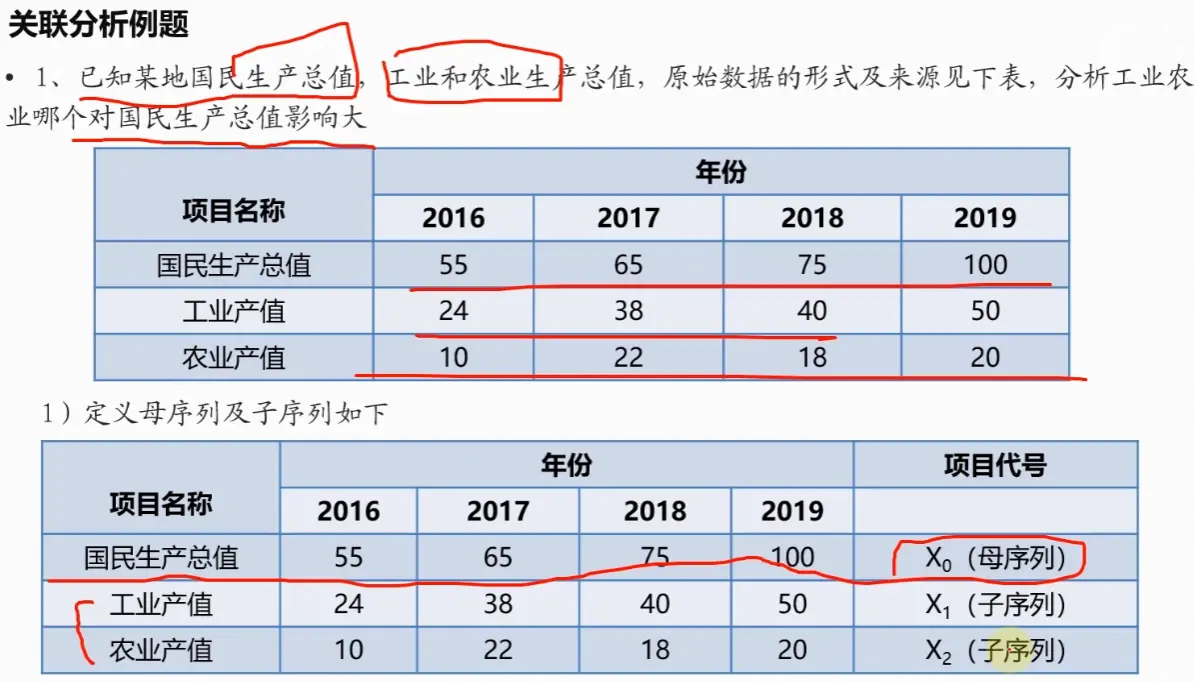
首先，需要明确研究的目标。在灰色关联分析中，我们将反映系统行为特征的数据序列称为参考序列或母序列，记为 $X_0$ 。而影响系统行为的因素组成的数据序列则称为比较序列或子序列，记为 $X_i$ (i=1, 2, …, n)

母序列 $X_0$ ：通常是代表我们最关心的一个指标的序列，例如，研究产品质量时，母序列就是产品合格率序列
子序列 $X_i$ ：是可能影响母序列的各个因素所构成的数据序列，例如，影响产品合格率的可能是原材料纯度、生产温度、工人熟练度等

在方法评价问题中，可以先将数据正向化（同TOPSIS），再选取每一评价项在所有评价对象中最大值组成母序列，子序列与母序列的关联度越高，则该评价对象越优

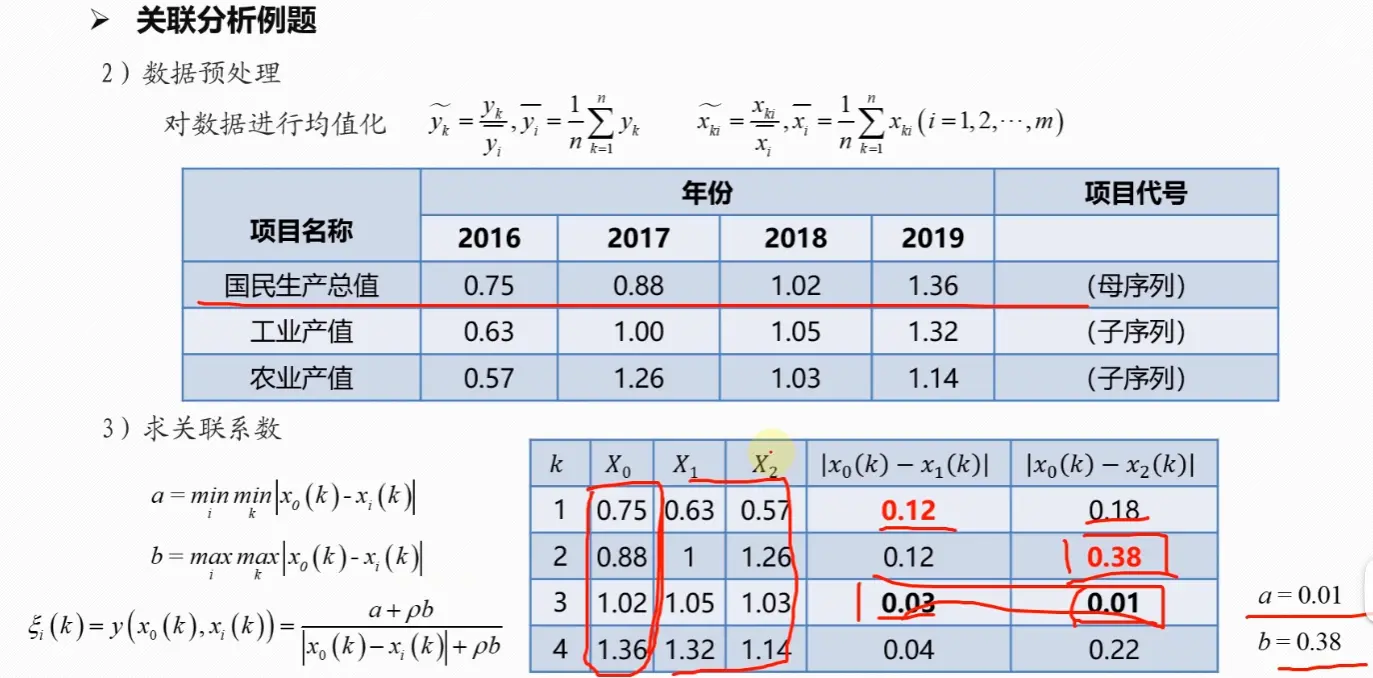
2. 数据无量纲化处理

由于各个子序列的单位和量纲可能不同，为了消除这种差异对结果的影响，需要对数据进行预处理，即无量纲化，方法是将序列中的每个数据都除以该序列的平均值

x_i^l(k) = \frac{x_i(k)}{\bar{x_i}}

其中 $\bar{x_i} = \frac{1}{m} \sum_{k=1}^m x_i(k)$ ， $m$ 为序列的长度

母序列和所有子序列都必须进行相同的无量纲化处理

3. 计算灰色关联系数

灰色关联系数用于表示在每个时间点上，子序列与母序列的关联程度。其计算公式如下：

\xi_i(k) = \frac{\min\limits_i \min\limits_k |x_0'(k) - x_i'(k)| + \rho \cdot \max\limits_i \max\limits_k |x_0'(k) - x_i'(k)|}{|x_0'(k) - x_i'(k)| + \rho \cdot \max\limits_i \max\limits_k |x_0'(k) - x_i'(k)|}

其中：

$x_0'(k)$ 是母序列在第 $k$ 个点的值
$x_i'(k)$ 是第 $i$ 个子序列在第 $k$ 个点的值
$|x_0'(k) - x_i'(k)|$ 是母序列与子序列在第 $k$ 点的绝对差
$\min\limits_i \min\limits_k |x_0'(k) - x_i'(k)|$ 是所有序列在所有点的绝对差中的最小值（两级最小差）
$\max\limits_i \max\limits_k |x_0'(k) - x_i'(k)|$ 是所有序列在所有点的绝对差中的最大值（两级最大差）
$\rho$ 是分辨系数，取值范围为 $(0, 1)$ 。 $\rho$ 的作用是提高关联系数之间的差异性。 $\rho$ 越小，分辨能力越强。通常情况下， $\rho$ 取值为0.5

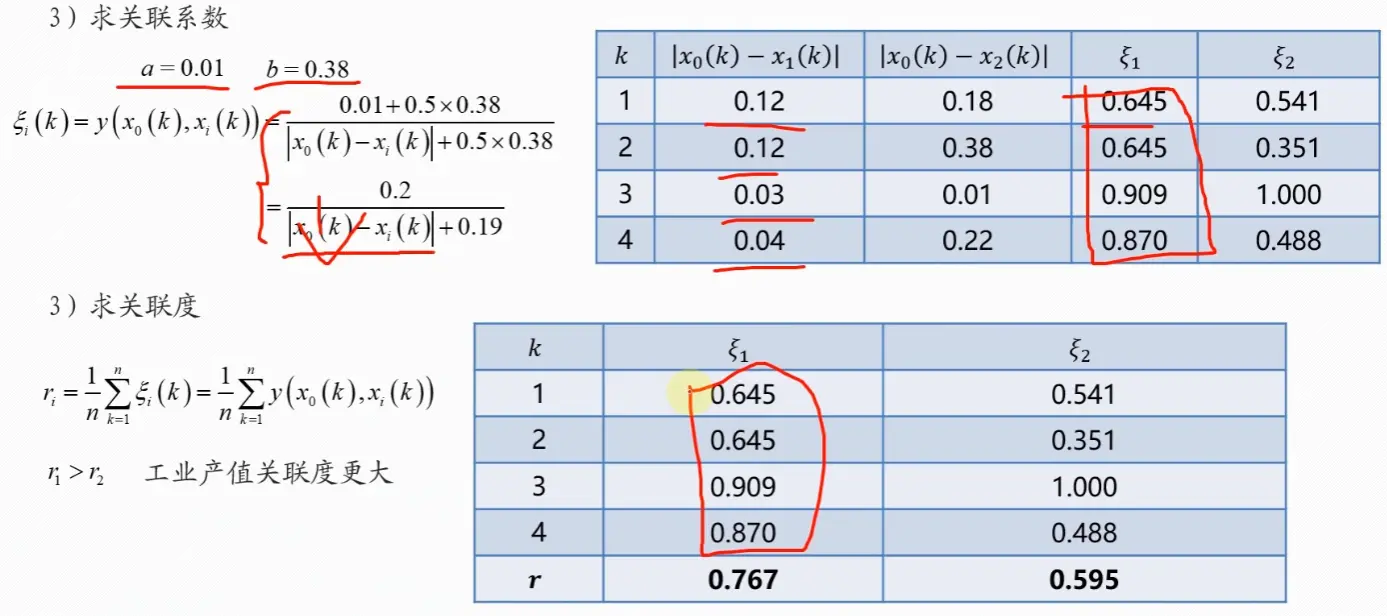
4. 计算计算灰色关联度

灰色关联度是所有时间点上关联系数的平均值，它综合地反映了子序列与母序列的关联程度。计算公式为：

\gamma_i = \frac{1}{m} \sum_{k=1}^m \xi_i(k)

其中：

$\gamma_i$ 是第 $i$ 个子序列对母序列的灰色关联度
$m$ 是序列的长度

5. 关联度排序与结论

计算出所有子序列的灰色关联度后：

根据关联度大小进行排序
关联度值越大，说明该子序列（因素）对母序列（目标）的影响越大
通过排序可以找出影响目标的关键因素

示例

示例代码

import pandas as pd
import numpy as np


def grey_relational_analysis(data, rho=0.5, method='mean'):
    """
    灰色关联分析 (Grey Relational Analysis, GRA) 函数

    该函数实现了灰色关联分析方法，用于衡量多个子序列与一个母序列之间的关联程度。
    适用于数学建模中进行多因素影响程度的分析。

    参数 (Args):
        data (pd.DataFrame):
            输入的数据框。
            格式要求：
            - 第一列 (index 0) 应为参考序列 (母序列)。
            - 后续列 (index 1, 2, ...) 应为比较序列 (子序列)。
            - 每一行代表一个观察点 (例如，年份、实验批次)。

        rho (float, optional):
            分辨系数，取值范围 (0, 1)，通常取 0.5。
            分辨系数越小，关联系数之间的差异越大，区分能力越强。默认为 0.5。

        method (str, optional):
            数据无量纲化的方法。
            - 'initial': 初值化处理 (序列的每个值除以第一个值)。适用于数据有明显增减趋势的情况。
            - 'mean': 均值化处理 (序列的每个值除以均值)。适用于数据波动平稳的情况。
            默认为 'initial'。

    返回 (Returns):
        pd.DataFrame:
            一个包含分析结果的数据框，包括：
            - 'GreyRelationalGrade': 每个子序列的灰色关联度。
            - 'Rank': 根据关联度降序排列的排名。
    """

    # 1. 数据预处理 (无量纲化)
    # ---------------------------------
    # 检查输入数据是否为DataFrame
    if not isinstance(data, pd.DataFrame):
        raise ValueError("输入数据必须是 pandas DataFrame 格式。")

    # 提取母序列和子序列
    ref_series = data.iloc[:, 0]
    comp_series = data.iloc[:, 1:]

    # 无量纲化
    if method == 'initial':
        # 初值化
        normalized_ref = ref_series / ref_series.iloc[0]
        normalized_comp = comp_series / comp_series.iloc[0, :]
    elif method == 'mean':
        # 均值化
        normalized_ref = ref_series / ref_series.mean()
        normalized_comp = comp_series / comp_series.mean()
    else:
        raise ValueError("无量纲化方法 'method' 只能是 'initial' 或 'mean'。")

    # 2. 计算母序列与子序列的差值序列
    # ---------------------------------
    # 使用numpy的广播机制来计算差的绝对值
    diff_series = np.abs(normalized_comp.values - normalized_ref.values.reshape(-1, 1))

    # 3. 计算两级最小差和最大差
    # ---------------------------------
    min_diff = np.min(diff_series)
    max_diff = np.max(diff_series)

    # 4. 计算灰色关联系数
    # ---------------------------------
    # 根据公式计算关联系数矩阵
    relational_coeffs = (min_diff + rho * max_diff) / (diff_series + rho * max_diff)

    # 5. 计算灰色关联度
    # ---------------------------------
    # 对每个子序列的关联系数求均值，得到关联度
    grey_relational_grade = relational_coeffs.mean(axis=0)

    # 6. 结果整理与输出
    # ---------------------------------
    # 创建结果DataFrame
    result_df = pd.DataFrame({
        'Factor': comp_series.columns,
        'GreyRelationalGrade': grey_relational_grade
    })

    # 按关联度降序排序
    result_df = result_df.sort_values(by='GreyRelationalGrade', ascending=False)

    # 添加排名
    result_df['Rank'] = range(1, len(result_df) + 1)

    # 将Factor列设为索引，方便查看
    result_df = result_df.set_index('Factor')

    return result_df


# --- 使用示例 ---
if __name__ == '__main__':
    # 假设我们研究影响地区生产总值(GDP)的因素
    # 数据来源为虚构，仅用于演示

    # 创建一个DataFrame
    # 第一列是母序列 (GDP)
    # 后续列是子序列 (影响因素)
    example_data = pd.DataFrame({
        '地区生产总值 (亿元)': [100, 110, 125, 145, 170, 200],
        '全社会固定资产投资 (亿元)': [30, 35, 42, 50, 60, 75],
        '社会消费品零售总额 (亿元)': [50, 55, 60, 70, 80, 95],
        '地方财政收入 (亿元)': [20, 22, 26, 30, 35, 42],
        '年末总人口 (万人)': [200, 202, 205, 208, 212, 215]
    }, index=['2018年', '2019年', '2020年', '2021年', '2022年', '2023年'])

    print("--- 原始数据 ---")
    print(example_data)
    print("\n" + "=" * 40 + "\n")

    # 调用函数进行灰色关联分析
    # 使用默认的 rho=0.5 和 method='mean'
    try:
        analysis_result = grey_relational_analysis(example_data)

        print("--- 灰色关联分析结果 ---")
        print(analysis_result)

        # 结果解读
        print("\n--- 结果解读 ---")
        best_factor = analysis_result.index[0]
        print(f"根据灰色关联度分析，与'{example_data.columns[0]}'关联度最高的因素是'{best_factor}'。")
        print("各因素的影响程度排序如下：")
        ranked_factors = " > ".join(analysis_result.index)
        print(ranked_factors)

    except ValueError as e:
        print(f"发生错误: {e}")

模糊综合评价法

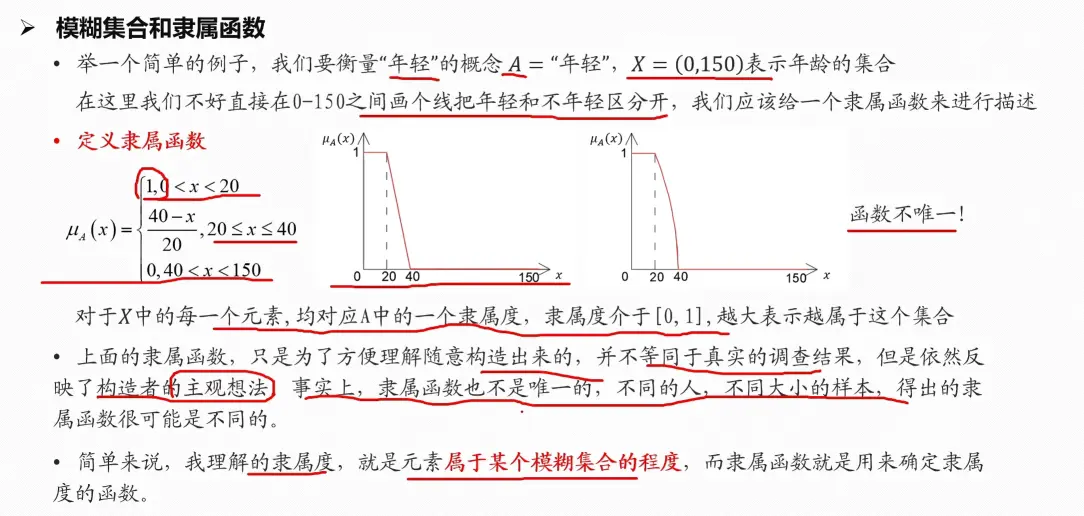
模糊集合与隶属函数

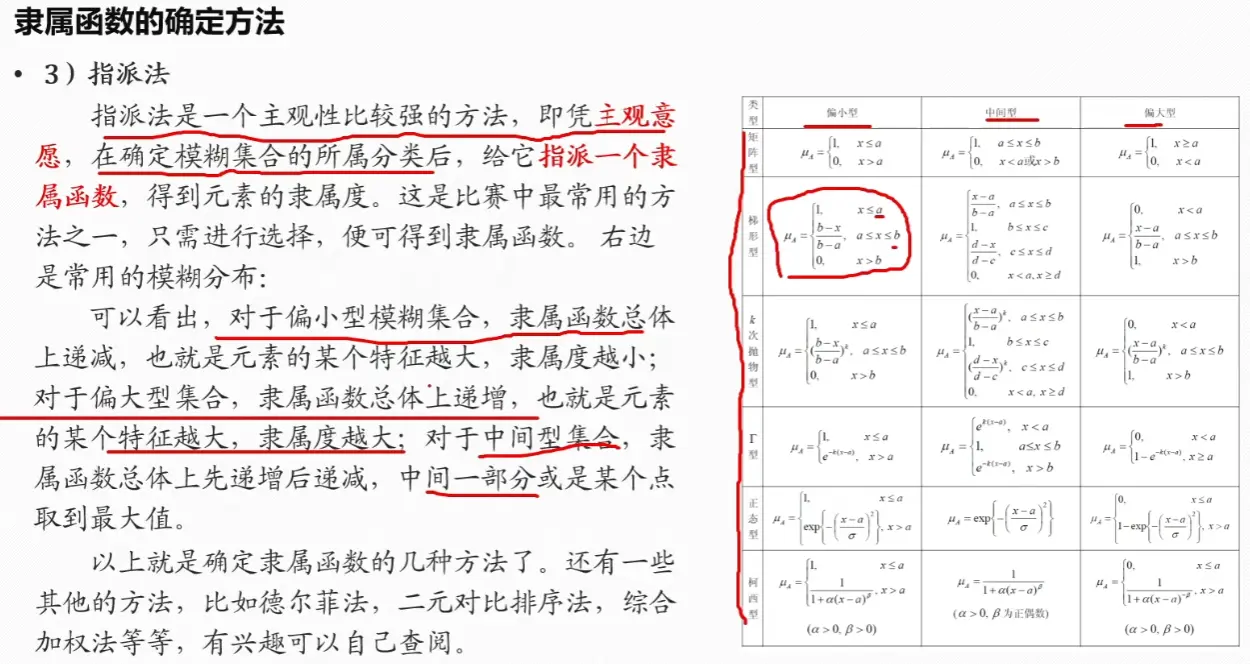
隶属函数的确定方法

评价步骤

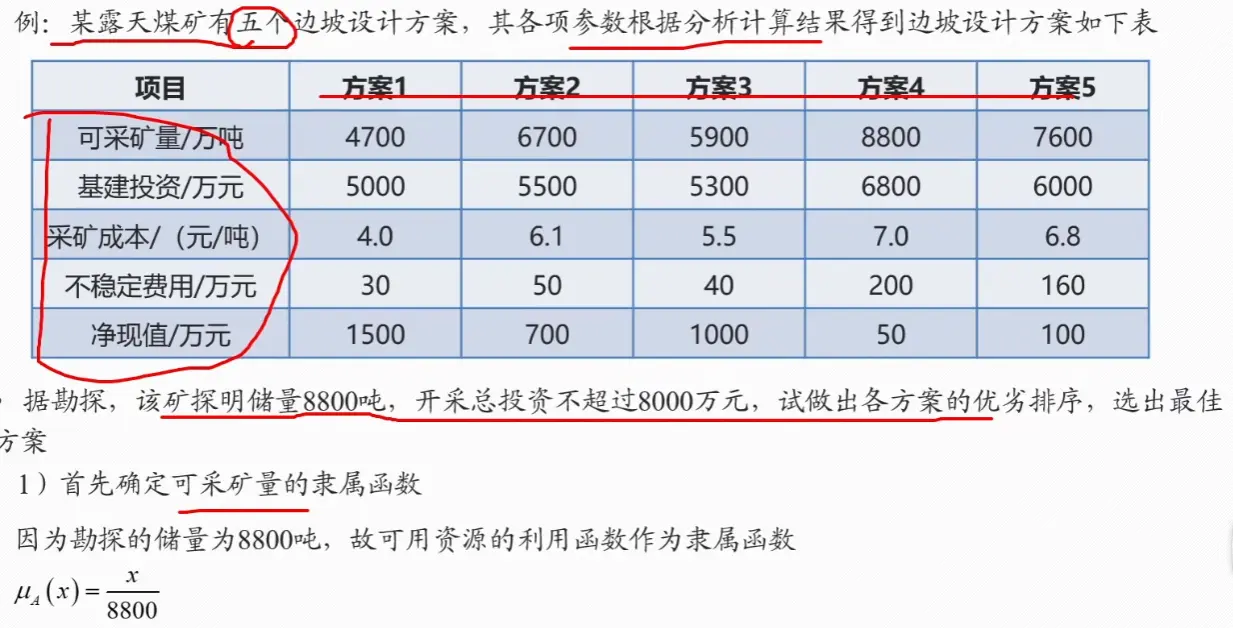
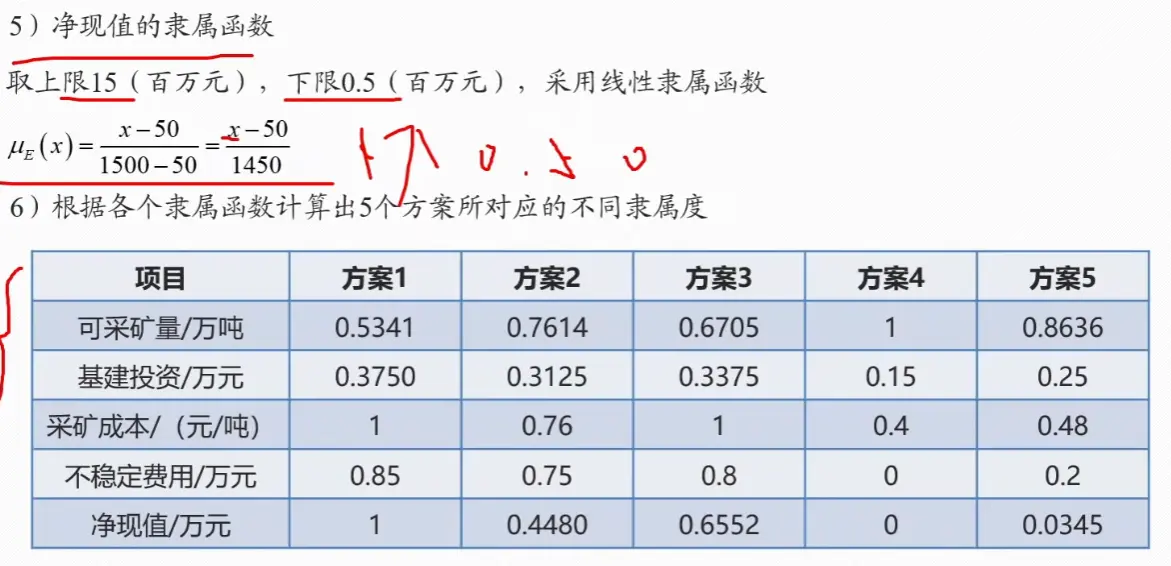
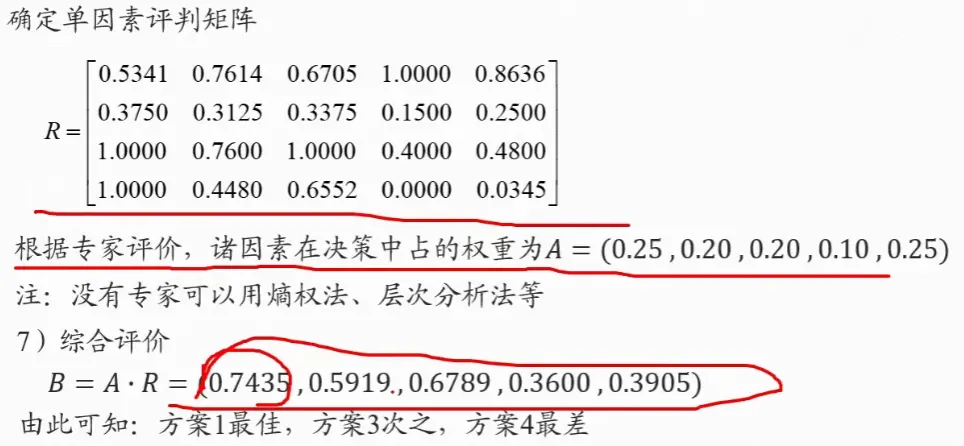
示例

示例一

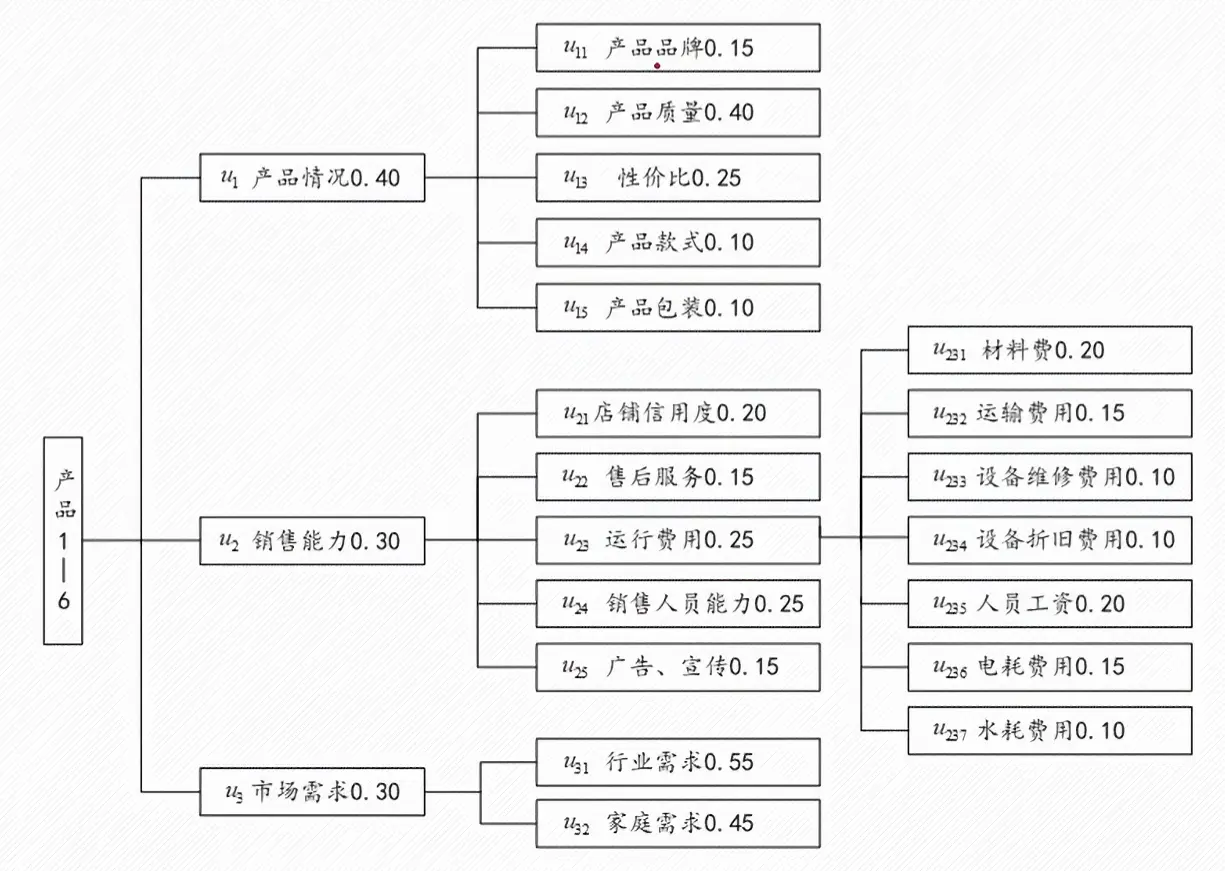
示例二

多层次模糊综合评价

示例

PCA 主成分分析

主成分分析（PCA）是一种被广泛应用的无监督学习算法，它能够在保留数据主要信息的前提下，对数据进行降维

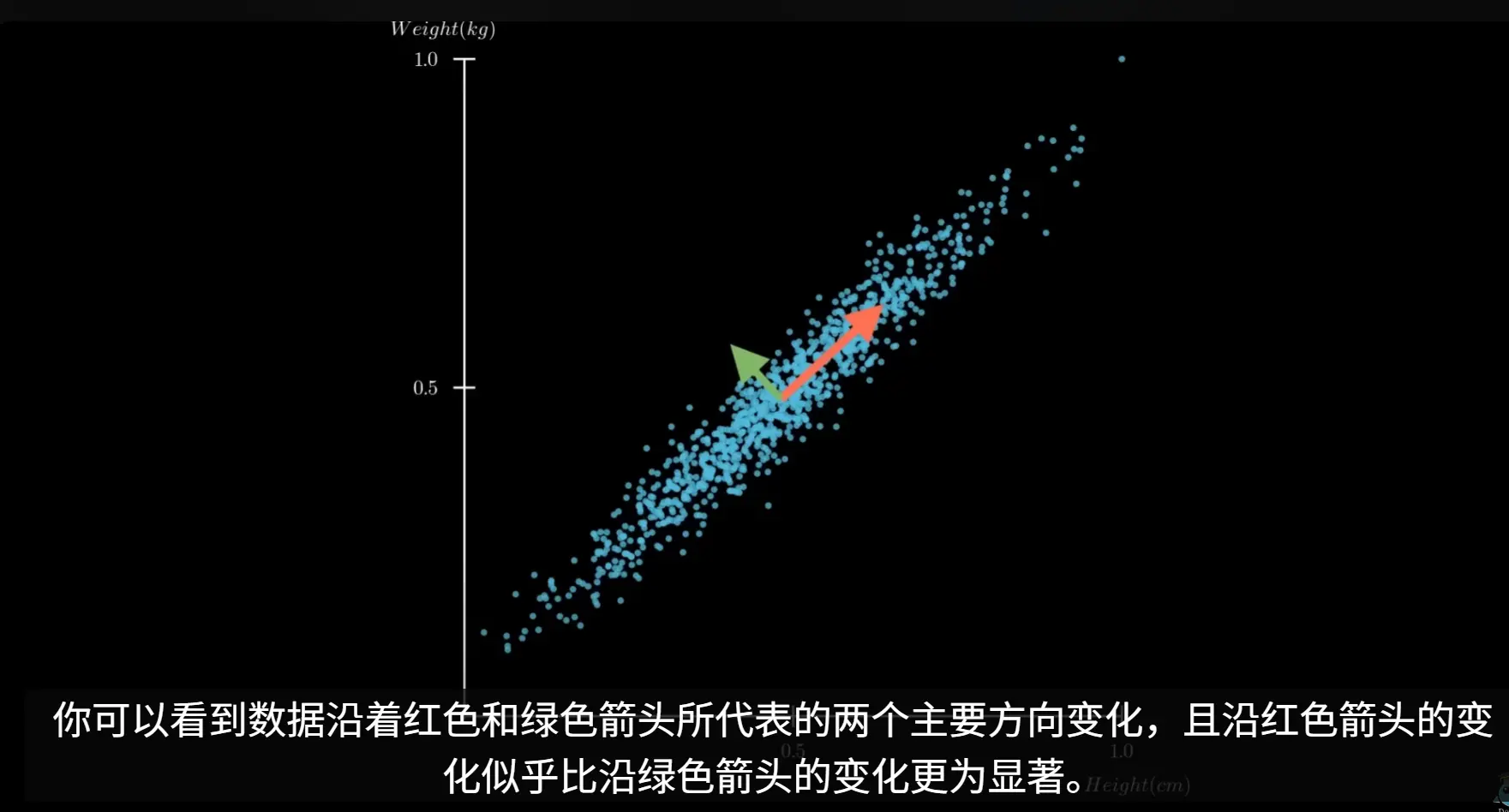
主成分分析（PCA）的核心思想是寻找数据中方差最大的方向，并将原始数据投影到这些方向上，形成新的、不相关的特征，即主成分。这些主成分是原始特征的线性组合，并且按照其所能解释的原始数据方差的大小进行排序。第一个主成分捕捉了数据中最大的方差，第二个主成分在与第一个主成分正交（不相关）的前提下捕捉了剩余方差中最大的部分，以此类推。

通过保留方差最大的前几个主成分，我们就可以在损失最少信息的情况下，实现数据的降维

核心步骤

假设我们有一个包含n个样本和m个特征的数据集 X：

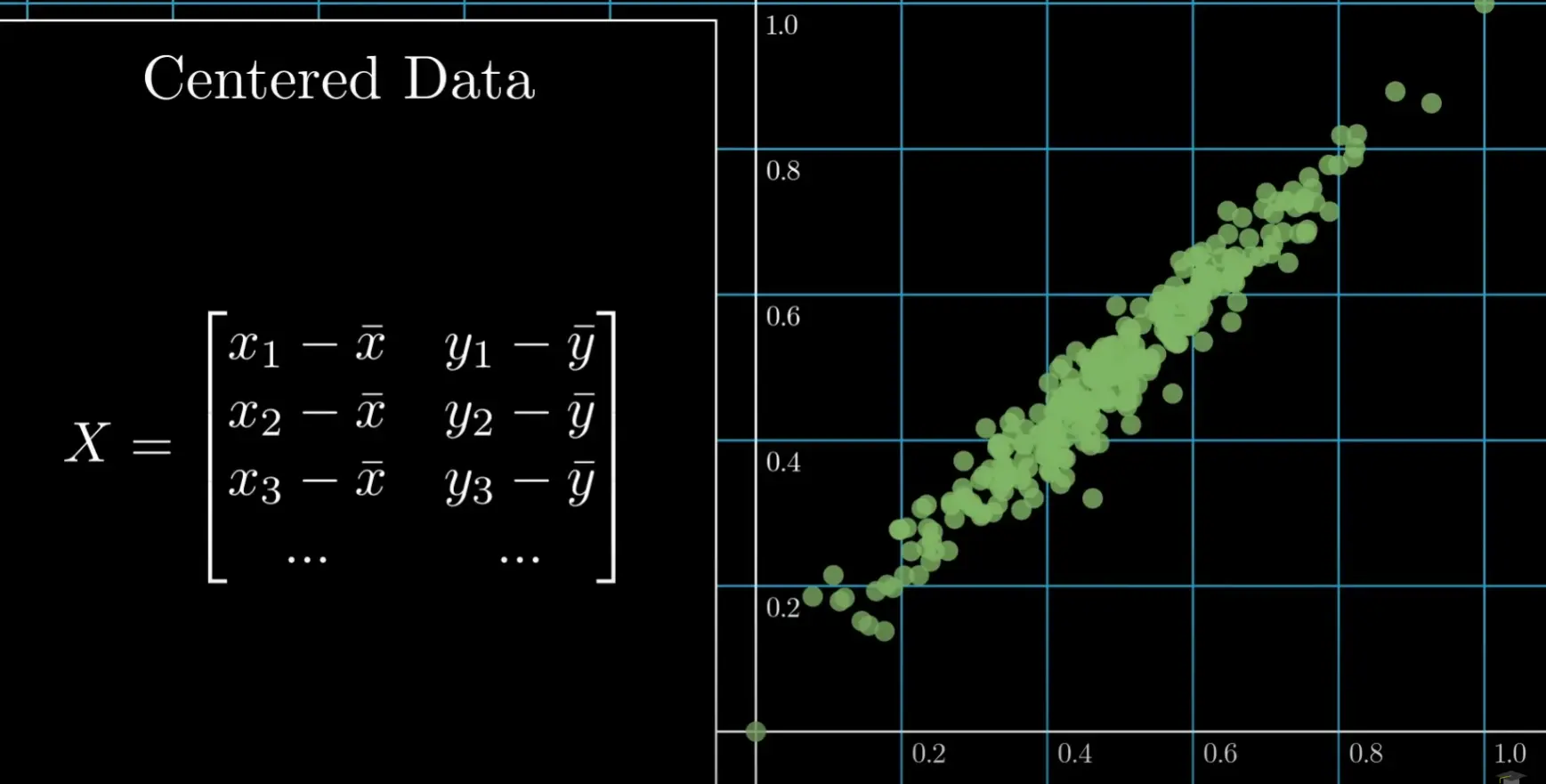
1. 数据预处理

对数据集 X 进行归一化处理，方法可以是计算每个变量的平均值，然后从每个数据点中减去该平均值

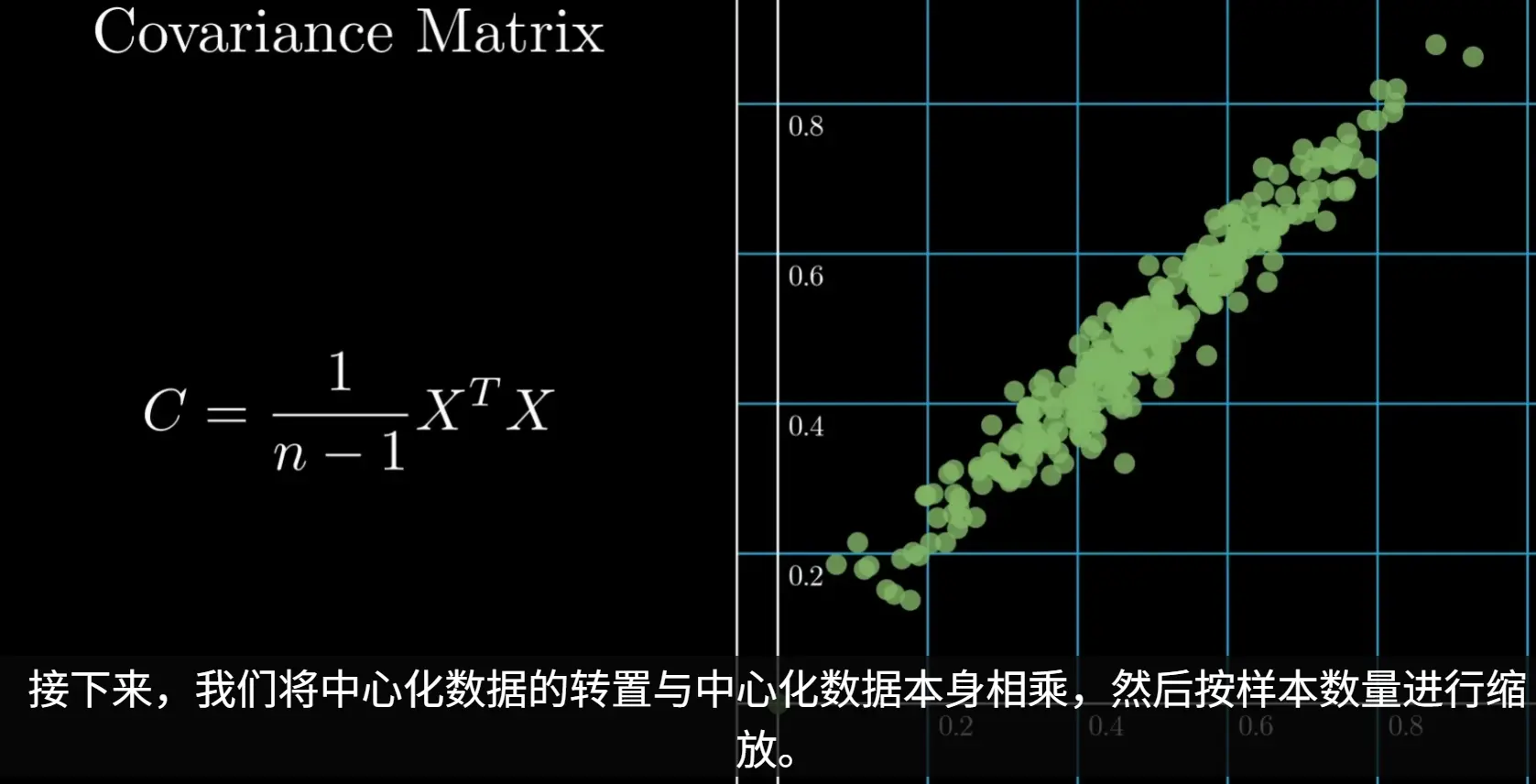
2. 计算协方差矩阵

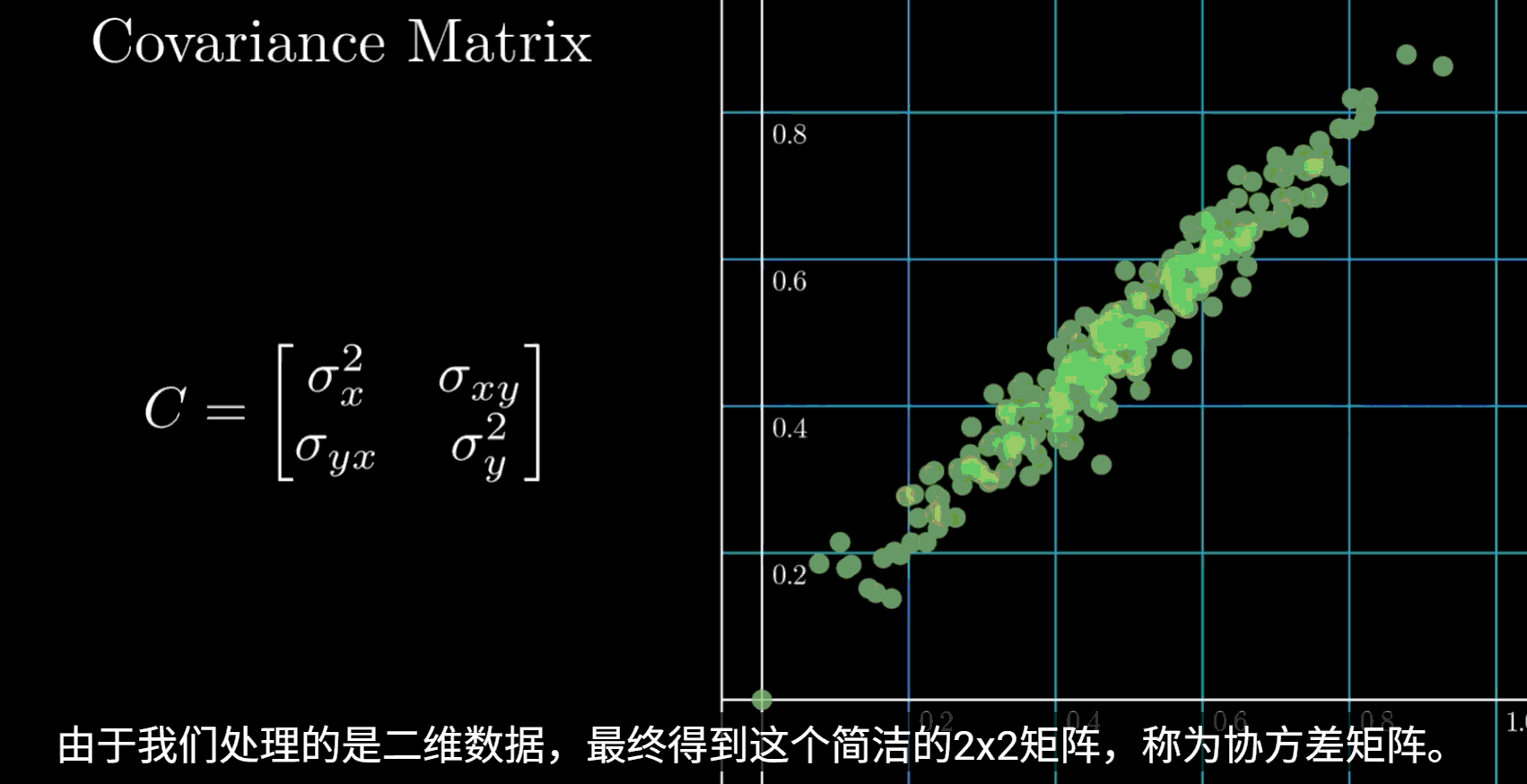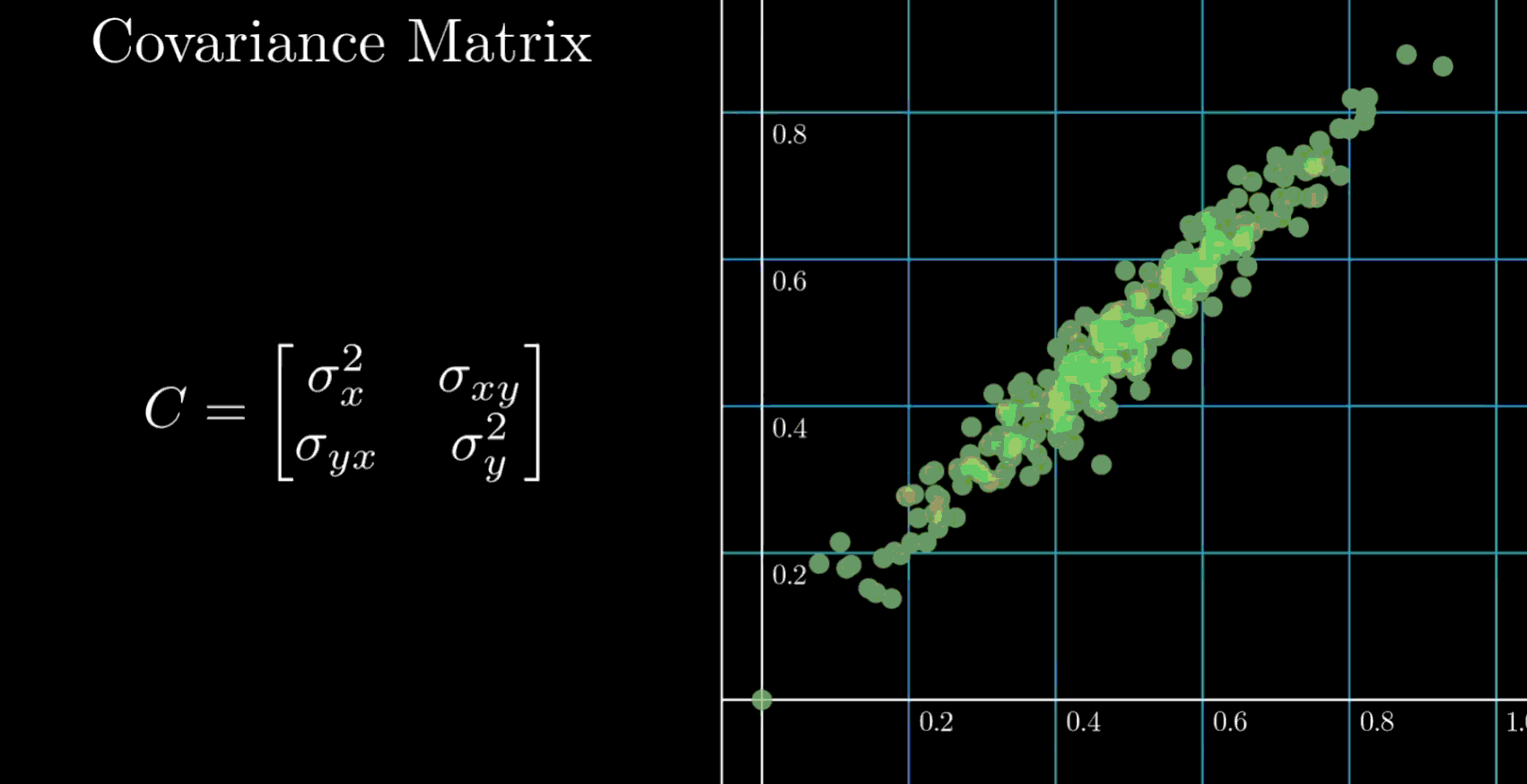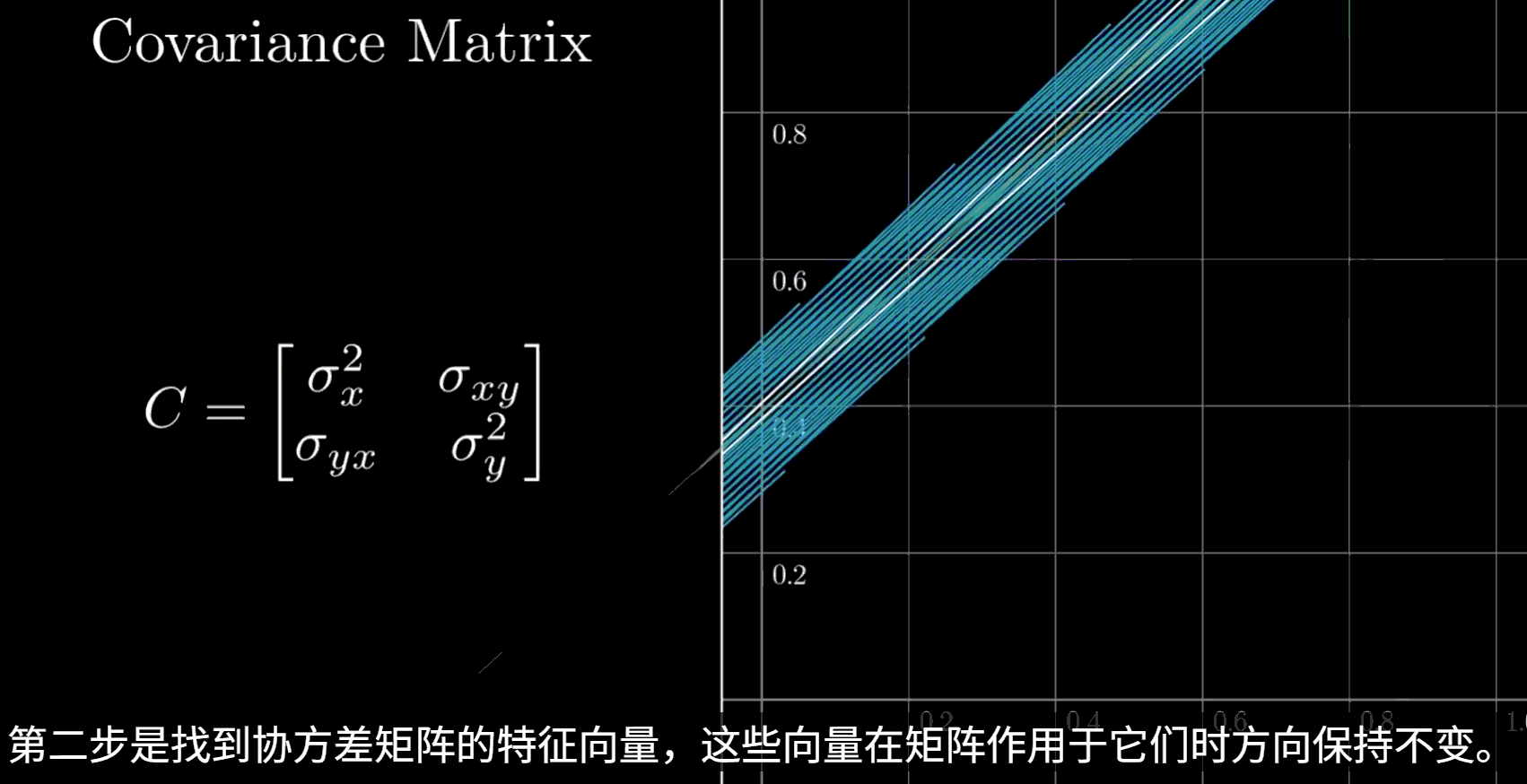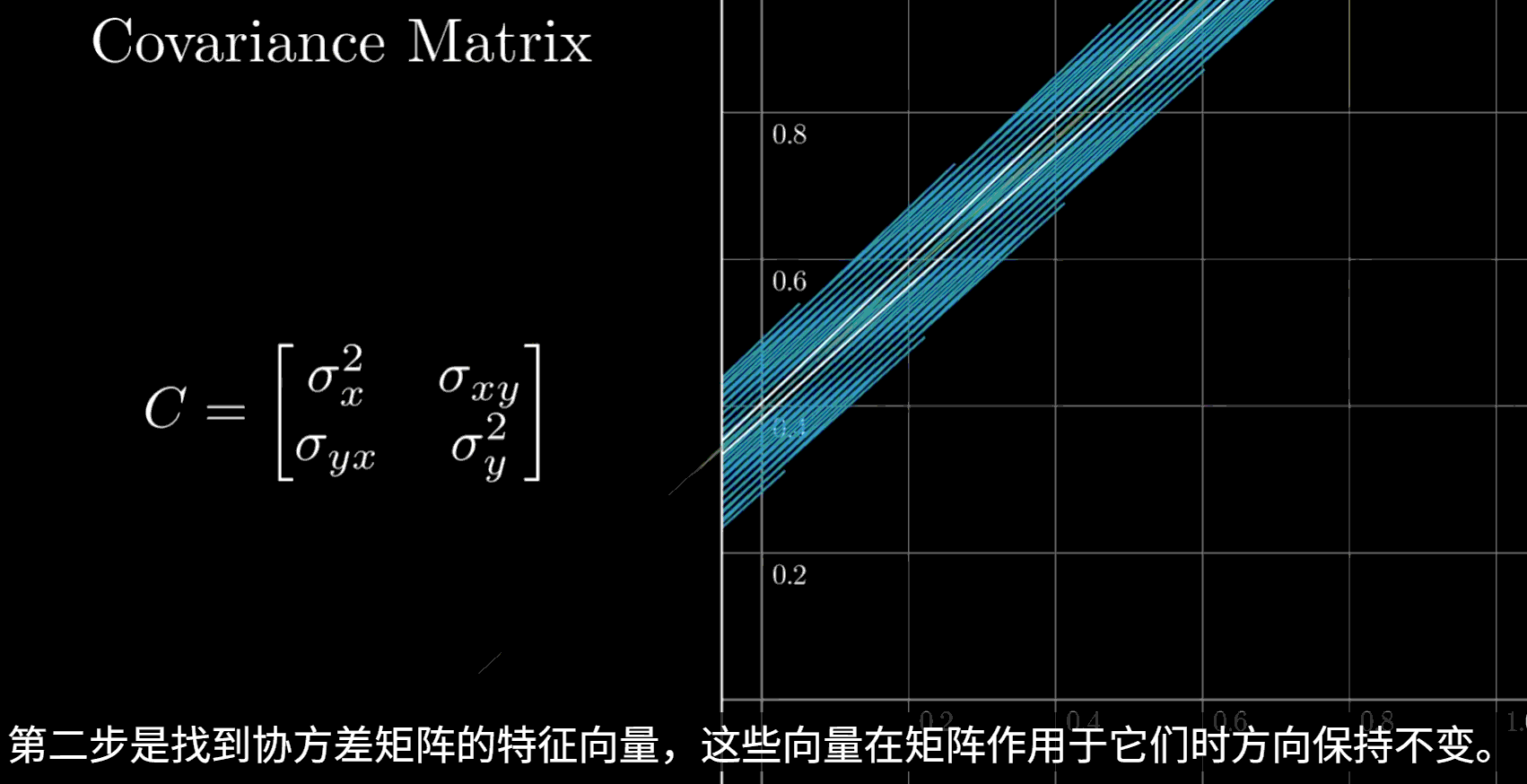
协方差矩阵衡量了不同特征之间的线性关系。矩阵的对角线元素是各个特征的方差，非对角线元素是不同特征之间的协方差

当数据为二维时

为什么样本方差/协方差的分母是 n-1？

在统计学和数据分析中，当我们计算一个样本的方差或协方差矩阵时，一个常见的问题是：为什么公式的分母是样本数量 n 减 1 (n-1)，而不是 n？

简而言之，答案是：使用 n-1 是为了得到对总体方差的“无偏估计”

这个修正方法在统计学上被称为贝塞尔校正 (Bessel’s Correction)。下面我们来详细拆解这个概念

核心问题：用样本估计总体

首先，我们必须明确我们在做什么。在绝大多数数据分析场景中，我们手头的数据只是一个样本 (Sample)，它是从一个更大的总体 (Population) 中抽取出来的。我们的最终目的，是希望通过分析这个样本来推断整个总体的特征

总体 (Population)：我们研究的全部对象的集合。例如，一个国家所有成年人的身高。总体的参数（如总体均值 $\mu$ 和总体方差 $\sigma^2$ ）是固定但通常未知的

样本 (Sample)：我们从总体中实际观测到的一部分数据。例如，随机抽取的 1000 名成年人的身高。我们通过计算样本的统计量（如样本均值 $\bar{x}$ 和样本方差 $s^2$ ）来估计总体的参数

偏差的来源：为何除以 n 会出错？

如果我们拥有整个总体的数据，并且知道总体的真实均值 $\mu$ ，那么计算总体方差的公式确实是除以 n：
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2$
然而，在现实中，我们几乎永远不可能知道总体的真实均值 $\mu$ 。因此，我们只能退而求其次，使用我们能计算出的样本均值 $\bar{x}$ 来替代它

问题就出在这里。一个样本中的数据点，离它们自身的均值 ( $\bar{x}$ ) 的离差平方和，总是小于或等于它们离总体真实均值 ( $\mu$ ) 的离差平方和。
$\sum_{i=1}^{n}(x_i - \bar{x})^2 \le \sum_{i=1}^{n}(x_i - \mu)^2$
这是因为样本均值 $\bar{x}$ 本身就是为了让这个平方和最小而计算出来的“中心点”，如果加入样本外的数据，总体均值 $\mu$ 不一定还等于 $\bar{x}$ 。因此，从样本数据扩展到总体数据时，如果我们仍用 $\bar{x}$ 来计算方差，并且仍然除以 n，离差平方和就偏小，我们得到的结果会系统性地、持续地低估真实的总体方差 $\sigma^2$ 。这种系统性的误差，在统计学上就称为偏差 (Bias)

解决方案：使用 n-1 进行无偏估计

为了修正这种系统性的低估，统计学家证明，我们应该用 n-1 来代替 n 作为分母

样本方差的无偏估计公式：
$s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2$
样本协方差的无偏估计公式：
$\text{Cov}(X, Y) = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})$
通过将分母减小（从 n 变为 n-1），我们人为地将计算结果调大了一点。这个调整的幅度恰好可以抵消掉由于使用样本均值 $\bar{x}$ 所带来的低估偏差

经过这样校正后，得到的样本方差 $s^2$ 就成了一个无偏估计量 (Unbiased Estimator)。这意味着，如果我们从同一个总体中反复抽取大量样本，并为每个样本都用 n-1 公式计算方差，那么所有这些样本方差的平均值将会非常接近真实的总体方差 $\sigma^2$

通过自由度直观解释：

最初，我们有 n 个独立的样本观测值，可以说我们有 n 个“自由度”，但是，为了计算方差，我们必须先计算出样本均值 $\bar{x}$ ，一旦样本均值 $\bar{x}$ 被确定下来，这 n 个样本值就失去了一部分“自由”，它们受到了一个约束：它们的总和必须等于 $n \times \bar{x}$
这意味着，如果我们知道了前 n-1 个样本值，可以通过样本均值计算出最后一个样本，那么最后一个样本值就完全被确定了，不再“自由”
因此，在估算样本的内部变异程度（即方差）时，真正能够提供独立信息的数据点只有 n-1 个

所有主流的科学计算库（如 Python 的 numpy.cov, pandas.DataFrame.cov 等）默认都是使用 n-1 来计算协方差的，正是因为它们的设计初衷是为了满足数据分析和推断性统计的需求

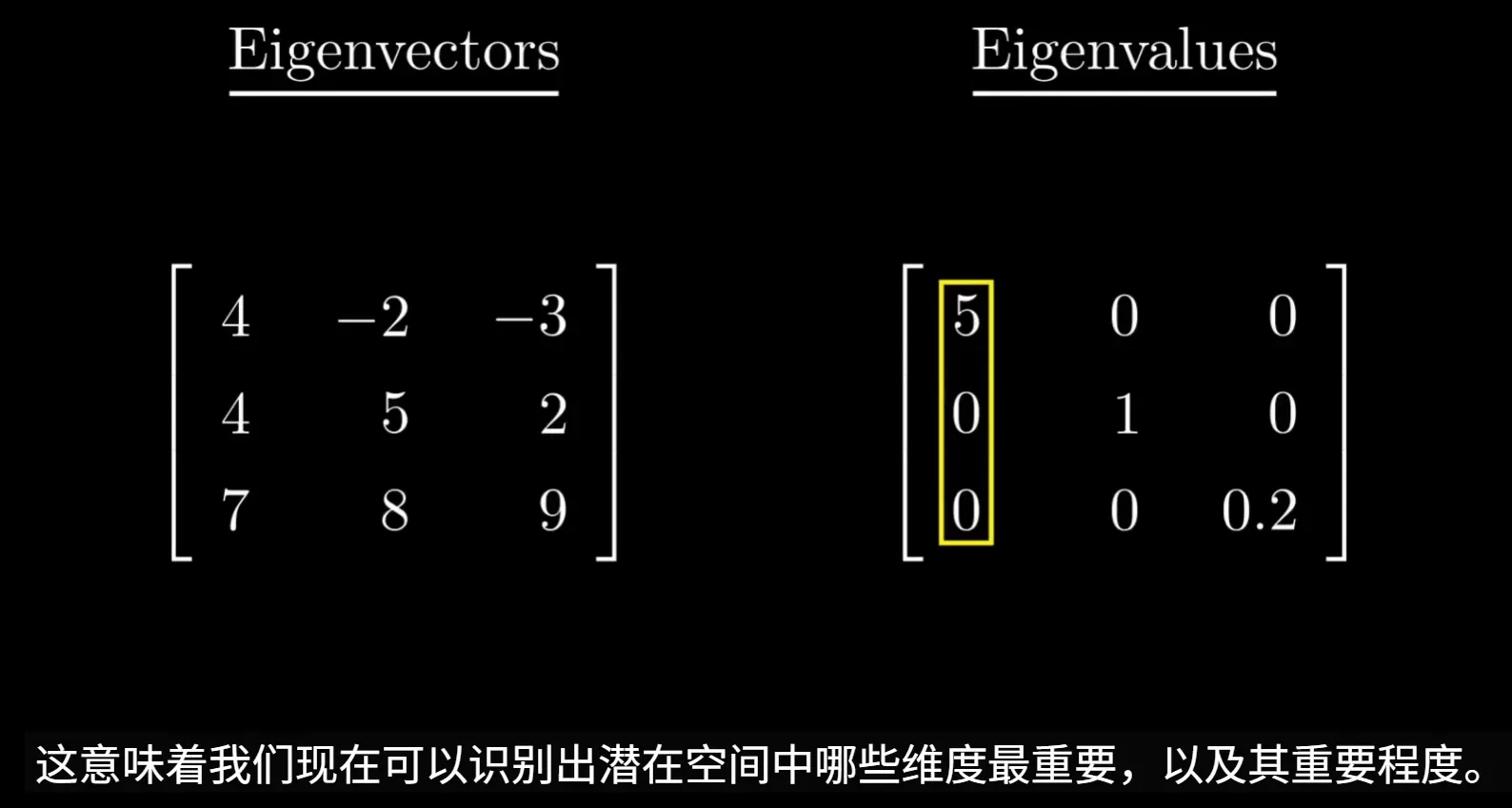
3. 计算特征值和特征向量

对协方差矩阵进行特征值分解

特征向量代表了主成分的方向，即数据方差最大的方向

特征值则表示在对应特征向量方向上数据的方差大小。特征值越大，说明该方向上的方差越大，包含的原始信息越多

该图数据仅作示例，实际计算得到的特征向量应该是单位正交的

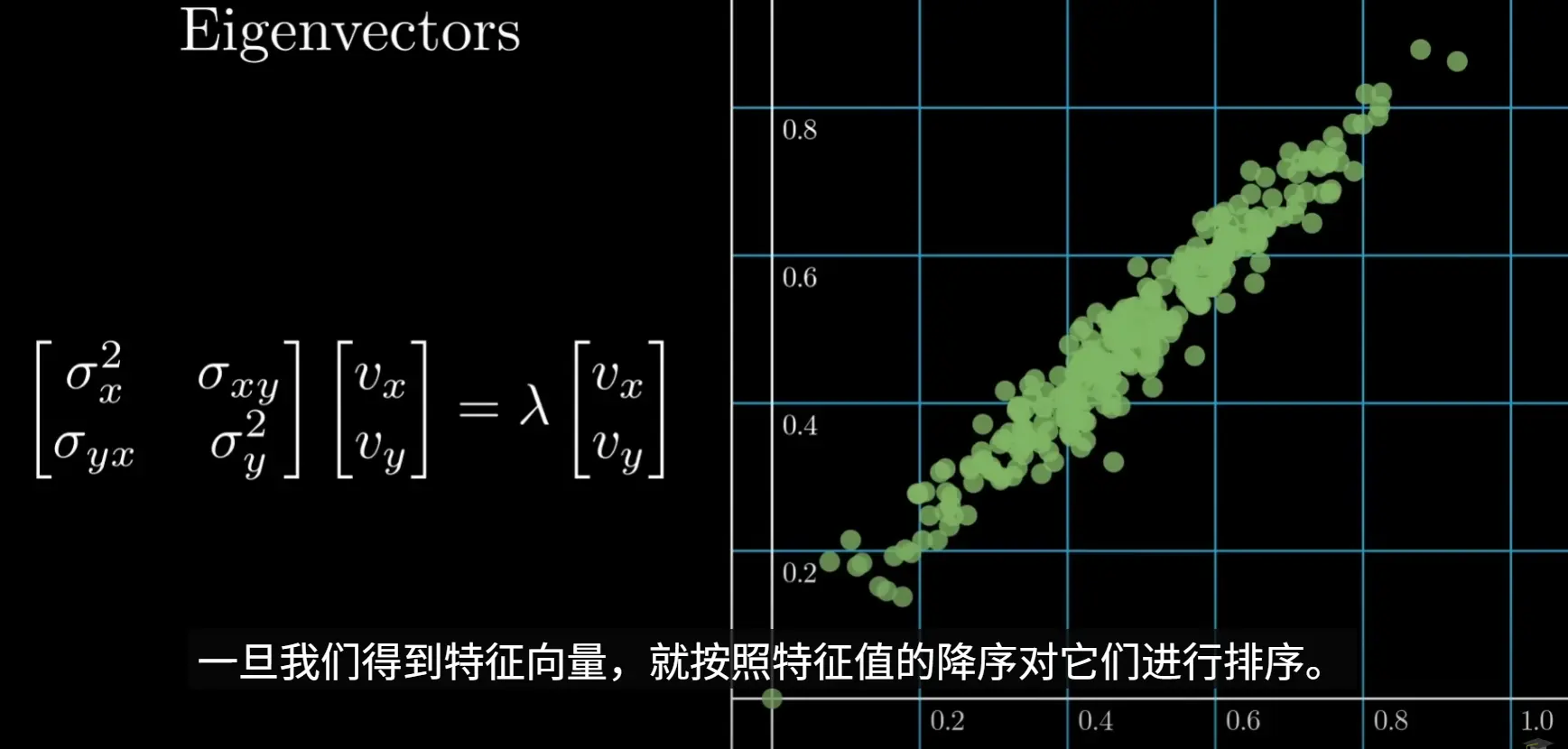
4. 选择主成分

将特征值从大到小排序，并选择其对应的特征向量。通常，我们会选择累计贡献率（即所选特征值之和占所有特征值之和的比例）达到一个阈值（如85%或95%）的前k个特征向量，选择这k个最大的特征值及其对应的特征向量，构成一个投影矩阵 P

5. 数据投影

将预处理后的数据 $X'$ 与投影矩阵 $P$ 相乘， $Z = X'P$ ，得到降维后的新数据集 $Z$ 。这个新数据集的维度为k，远小于原始数据的维度将原始中心化数据 X

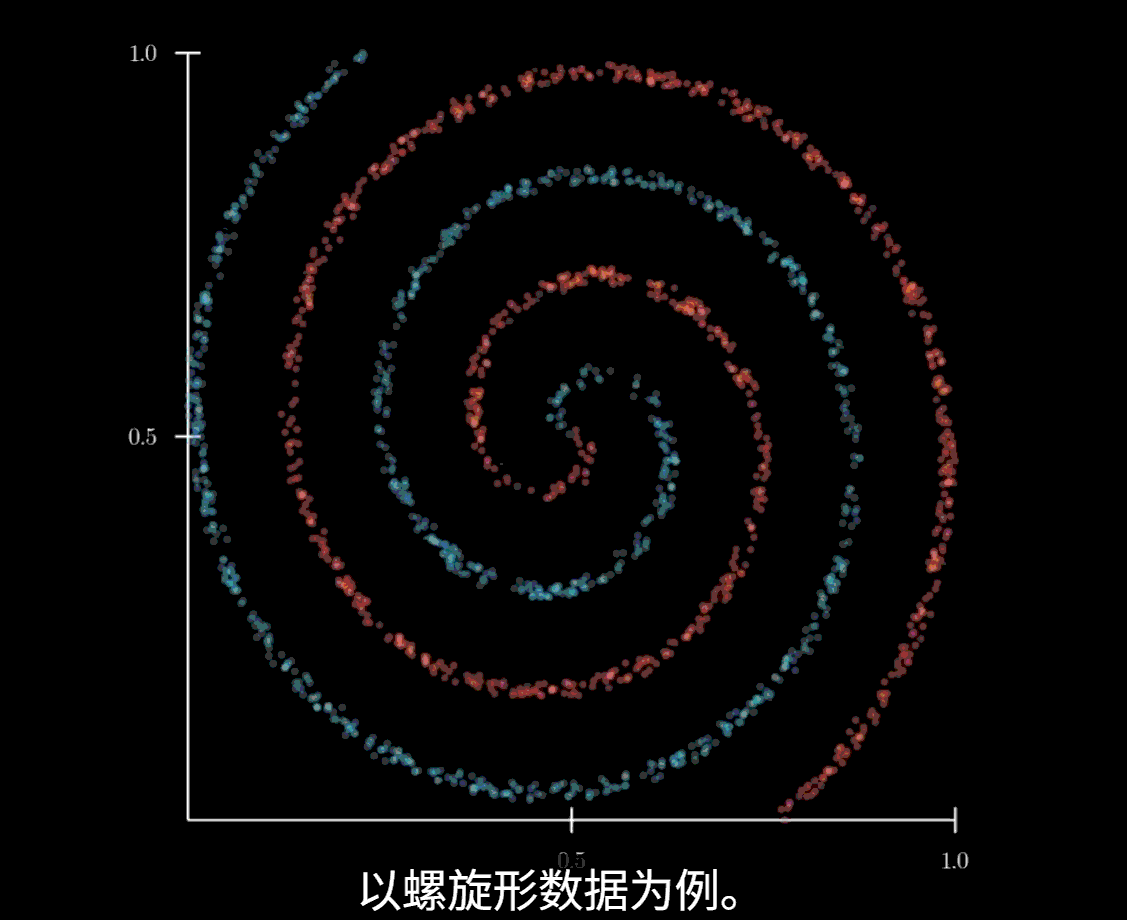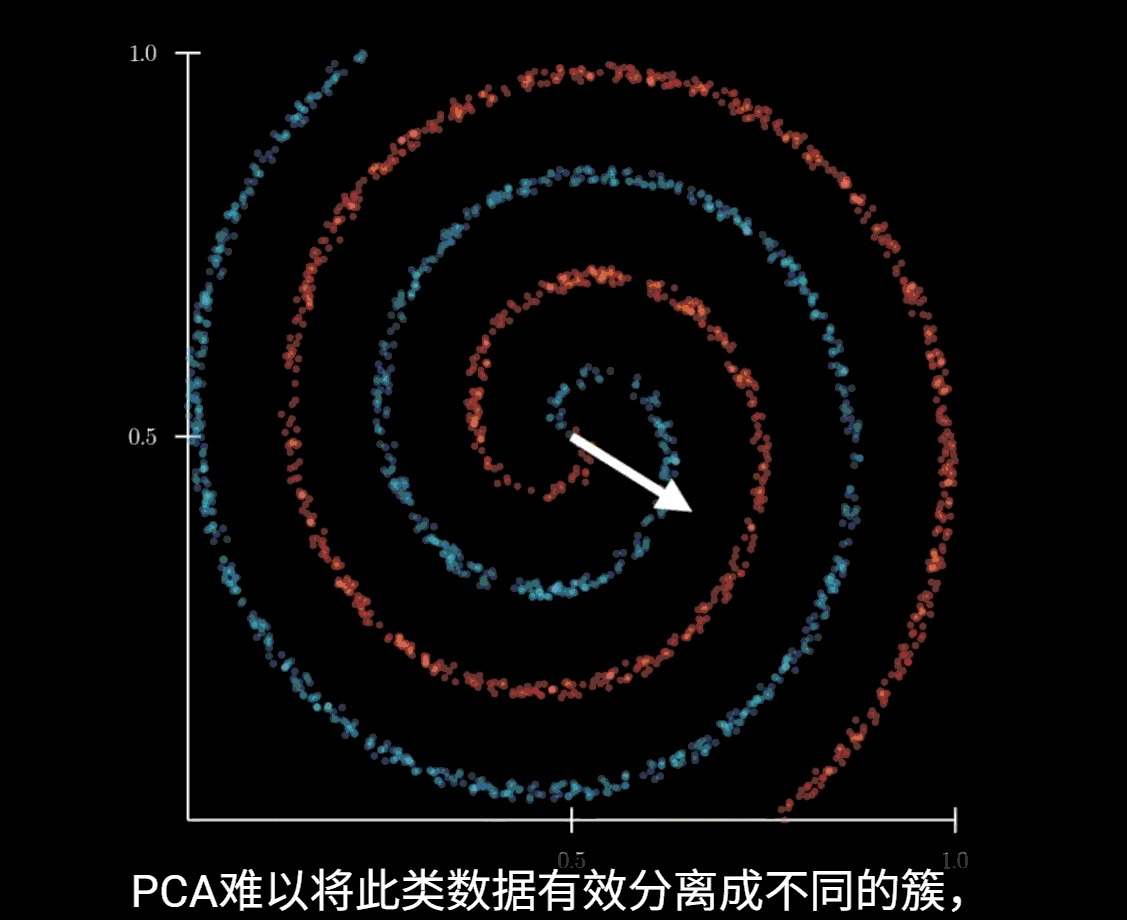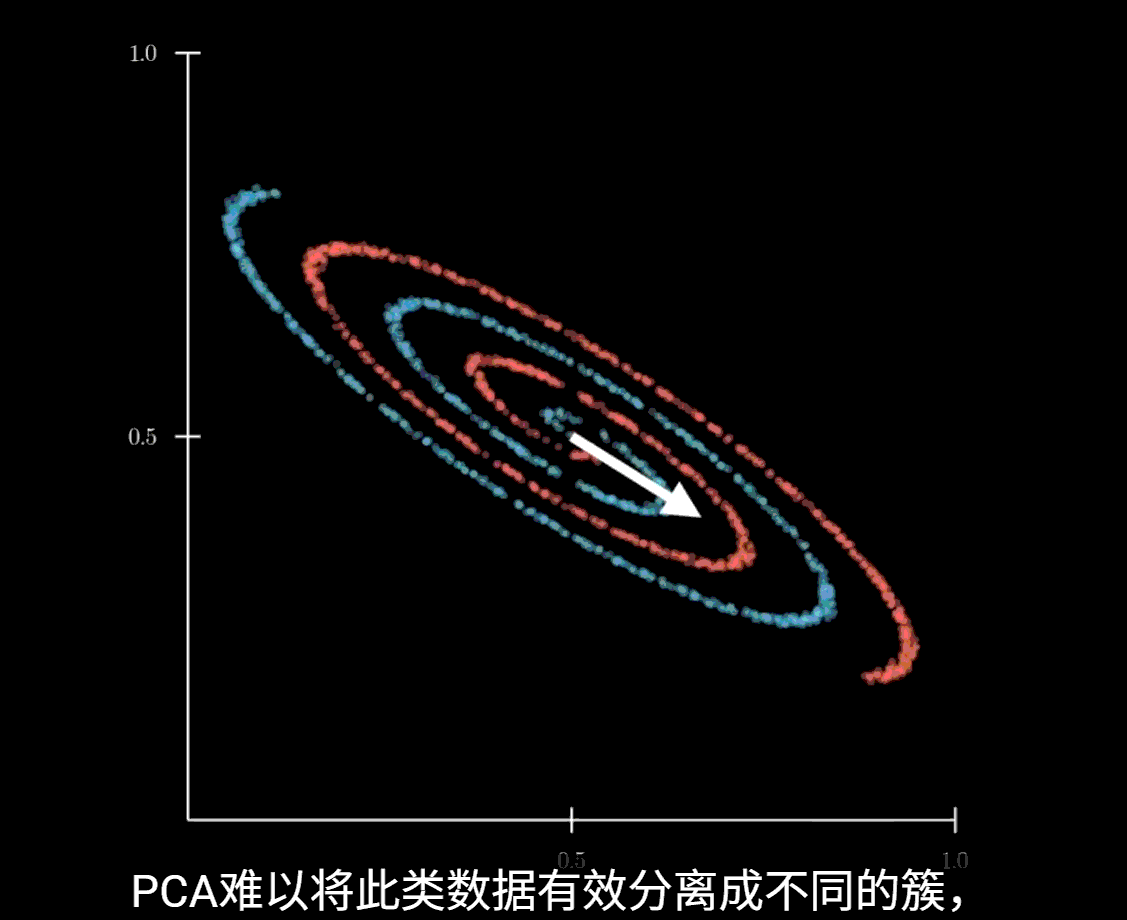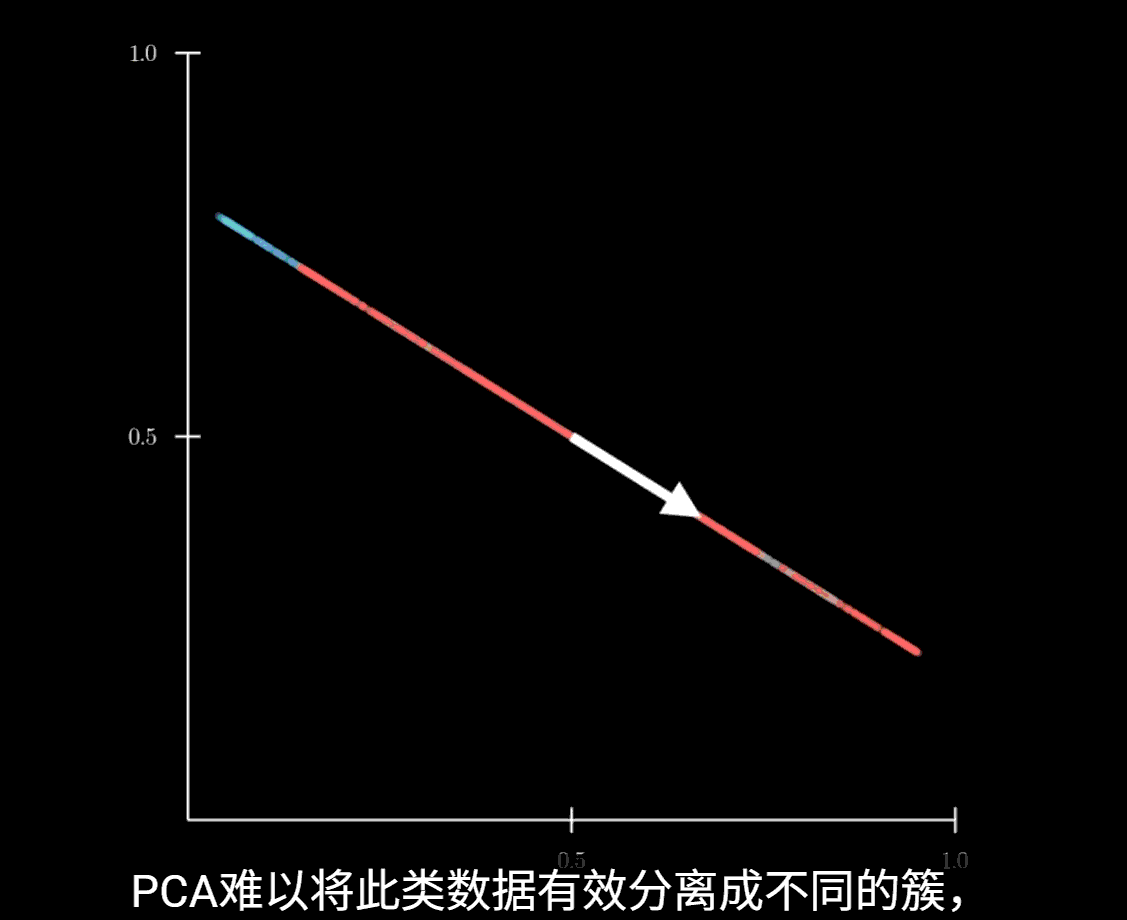
局限性

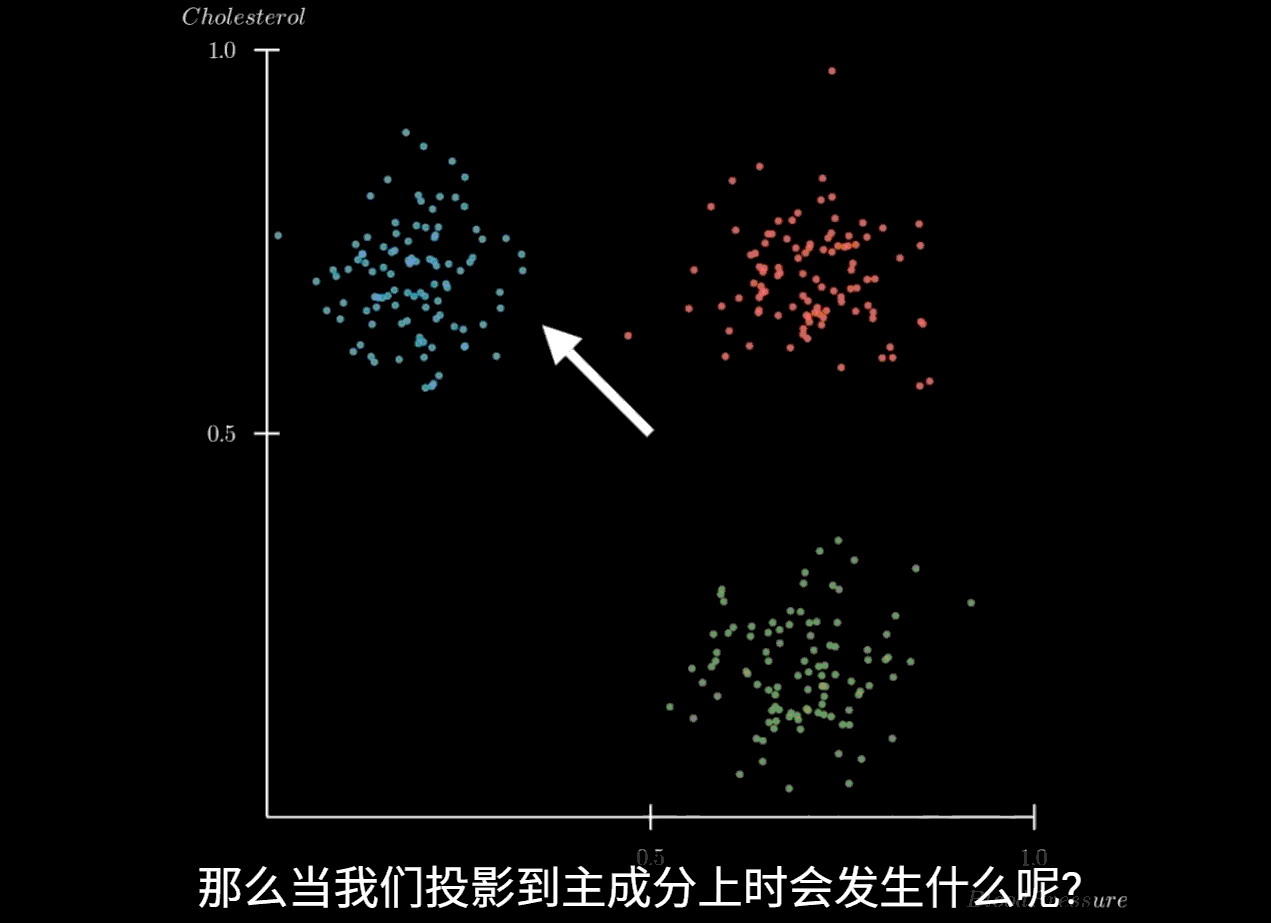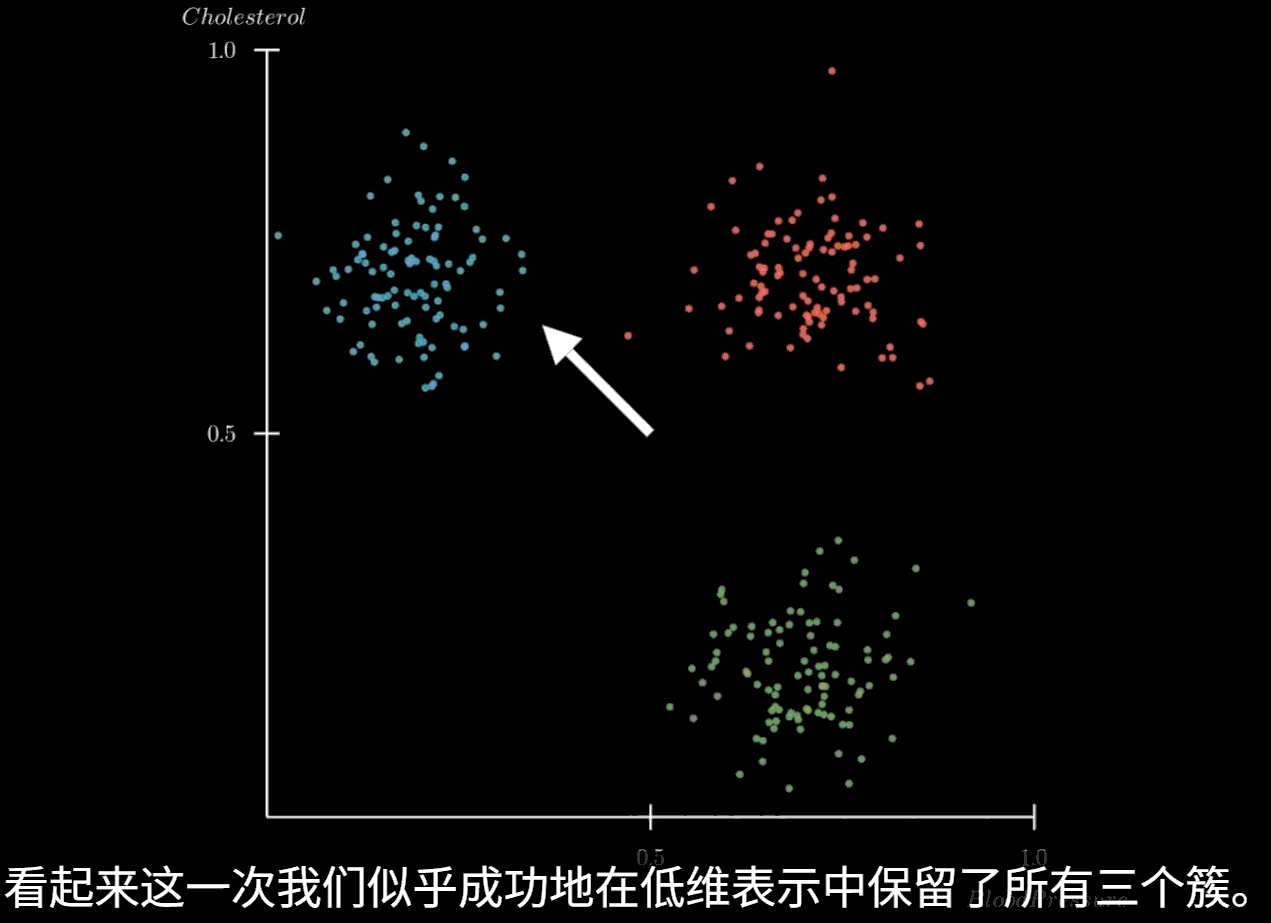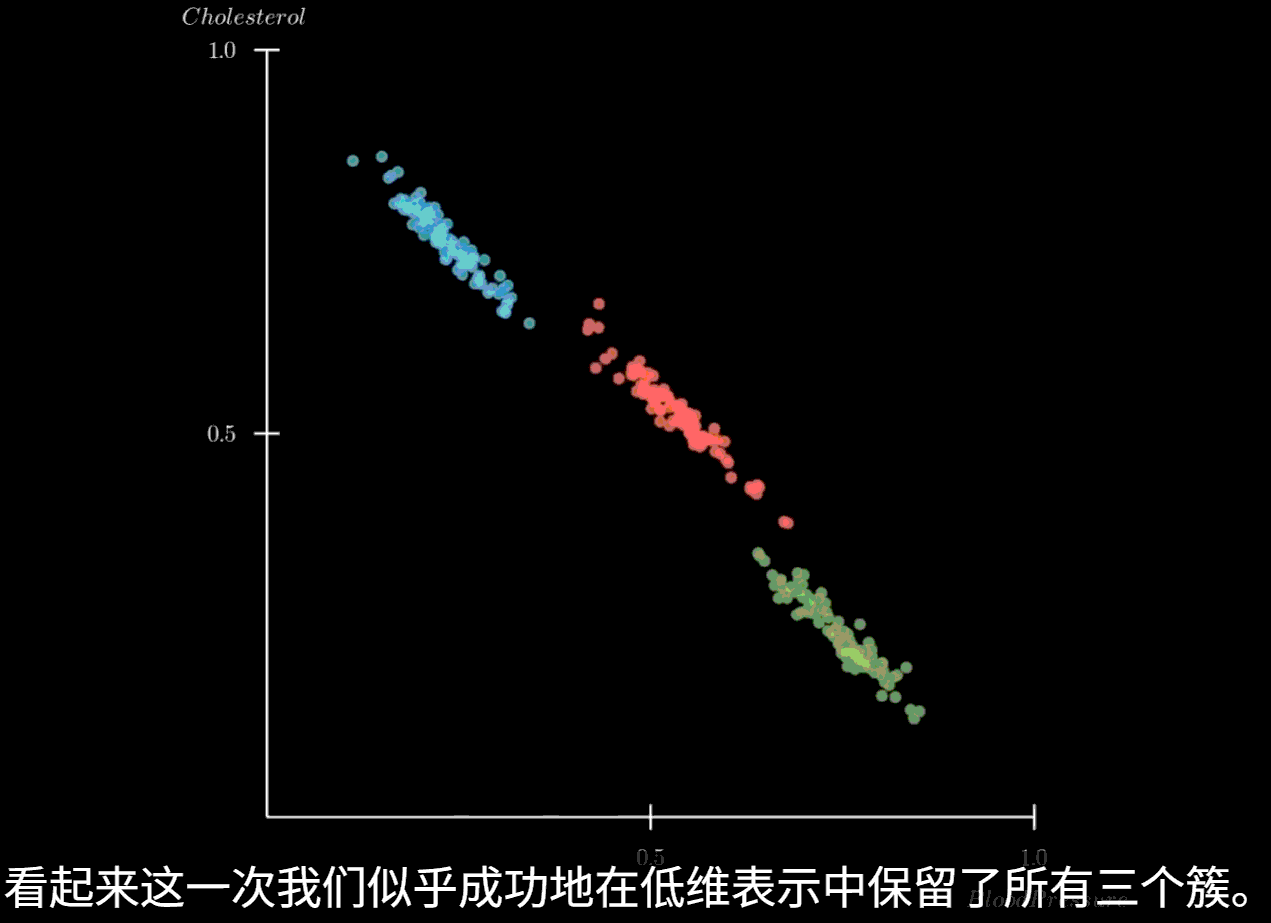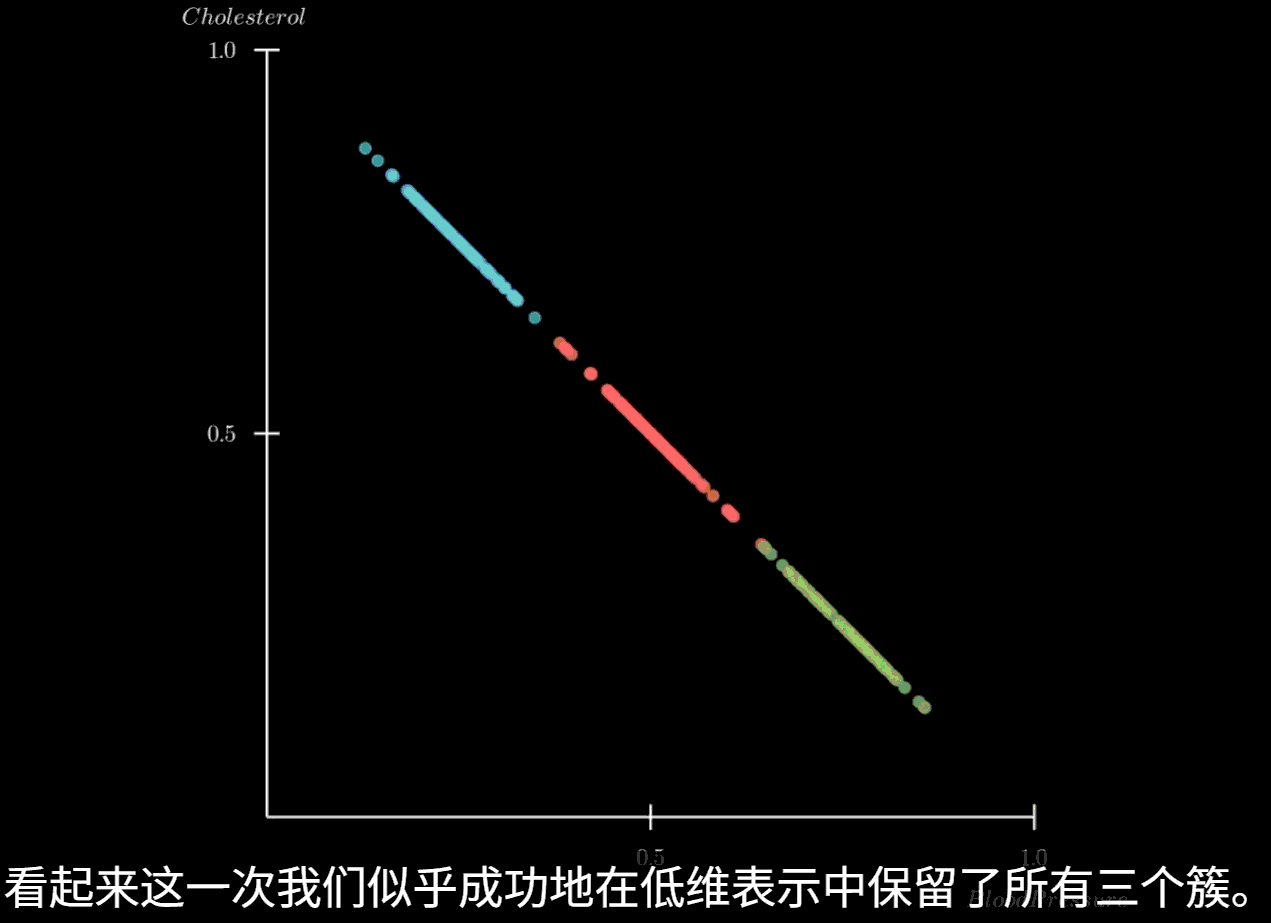
该方法依赖线性投影，当数据是非线性的时候，PCA难以带来较好的效果

此时应使用UMAP等

示例代码

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

class PCAModel:
    """
    一个用于主成分分析（PCA）的类。

    这个类封装了PCA的核心步骤，包括数据标准化、计算协方差矩阵、
    求解特征值与特征向量，以及将数据投影到主成分上。
    它的API设计模仿了scikit-learn，便于集成到机器学习工作流中。

    参数:
    n_components (int): 希望保留的主成分数量（即降维后的维度）。
    """

    def __init__(self, n_components):
        """初始化PCA模型"""
        self.n_components = n_components
        self.components_ = None  # 存储主成分（投影矩阵）
        self.mean_ = None  # 存储训练数据的均值，用于转换新数据
        self.explained_variance_ratio_ = None  # 存储每个主成分的方差贡献率

    def fit(self, X):
        """
        根据输入数据X来训练PCA模型。

        这个方法会计算出主成分，并存储它们以备后续转换使用。

        参数:
        X (np.ndarray): 训练数据，形状为 (n_samples, n_features)。
                        n_samples是样本数量，n_features是特征数量。
        """
        print("--- 开始PCA拟合过程 ---")
        # 1. 数据中心化
        self.mean_ = np.mean(X, axis=0)
        X_centered = X - self.mean_
        print("步骤1: 数据中心化完成。")
        print("数据均值 (self.mean_):\n", self.mean_)
        # print("中心化后的数据 (前5行):\n", X_centered[:5])
        print("-" * 20)

        # 2. 计算协方差矩阵
        # 注意：如果特征数量 > 样本数量，直接在X_centered上做SVD会更高效。
        # 这里我们使用标准方法。np.cov的rowvar=False表示列代表变量。
        cov_matrix = np.cov(X_centered, rowvar=False)
        print("步骤2: 协方差矩阵计算完成。")
        print("协方差矩阵 (shape: {}):\n".format(cov_matrix.shape), cov_matrix)
        print("-" * 20)

        # 3. 计算协方差矩阵的特征值和特征向量
        eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
        print("步骤3: 特征值和特征向量计算完成。")
        print("特征值 (Eigenvalues):\n", eigenvalues)
        print("特征向量 (Eigenvectors):\n", eigenvectors)
        print("-" * 20)

        # 4. 对特征值和特征向量进行排序
        # 从大到小排序特征值，并获取对应的索引
        sorted_indices = np.argsort(eigenvalues)[::-1]
        sorted_eigenvalues = eigenvalues[sorted_indices]
        sorted_eigenvectors = eigenvectors[:, sorted_indices]
        print("步骤4: 特征值和特征向量排序完成。")
        print("排序后的特征值:\n", sorted_eigenvalues)
        print("排序后的特征向量:\n", sorted_eigenvectors)
        print("-" * 20)

        # 5. 选择前k个主成分
        self.components_ = sorted_eigenvectors[:, :self.n_components]
        print(f"步骤5: 选择前 {self.n_components} 个主成分构成投影矩阵。")
        print("投影矩阵 (self.components_):\n", self.components_)
        print("-" * 20)

        # (可选) 计算并存储方差贡献率
        total_variance = np.sum(sorted_eigenvalues)
        self.explained_variance_ratio_ = sorted_eigenvalues[:self.n_components] / total_variance
        print("--- PCA拟合过程结束 ---\n")
        return self

    def transform(self, X):
        """
        使用训练好的PCA模型来转换数据X。

        参数:
        X (np.ndarray): 需要转换的数据，形状为 (n_samples, n_features)。

        返回:
        np.ndarray: 降维后的数据，形状为 (n_samples, n_components)。
        """
        if self.mean_ is None or self.components_ is None:
            raise RuntimeError("在调用transform之前必须先调用fit方法。")

        # 使用训练时计算的均值来中心化新数据
        X_centered = X - self.mean_

        # 6. 将数据投影到主成分上
        X_transformed = np.dot(X_centered, self.components_)

        return X_transformed

    def fit_transform(self, X):
        """
        训练模型并对同一数据进行转换。

        参数:
        X (np.ndarray): 需要训练和转换的数据。

        返回:
        np.ndarray: 降维后的数据。
        """
        self.fit(X)
        return self.transform(X)


# --- 如何使用 PCAModel 类的示例 ---
if __name__ == '__main__':
    # 1. 生成分布呈三角形的示例数据
    print("--- 生成示例数据 ---")
    np.random.seed(44)

    # *** 修改点：生成在三维空间中呈三角形分布的数据 ***
    # a. 在2D潜在空间中定义一个三角形的顶点
    triangle_vertices = np.array([
        [0, 0],
        [15, 2],
        [7, 12]
    ])

    # b. 使用重心坐标法在三角形内部生成均匀分布的点
    n_samples = 250
    s = np.random.rand(n_samples, 1)
    t = np.random.rand(n_samples, 1)

    # 确保点在三角形内
    outside = s + t > 1
    s[outside] = 1 - s[outside]
    t[outside] = 1 - t[outside]

    # 计算2D点的位置，这是我们的潜在变量
    latent_vars = (1 - s - t) * triangle_vertices[0] + s * triangle_vertices[1] + t * triangle_vertices[2]

    # c. 将2D点映射到3D空间并添加噪声
    # 定义一个旋转/映射矩阵
    mapping_matrix = np.array([
        [0.6, 0.4],
        [-0.5, 0.8],
        [0.7, -0.2]
    ])

    noise = np.random.normal(0, 0.8, (n_samples, 3))  # 噪声可以调小一点让形状更明显
    original_data = latent_vars.dot(mapping_matrix.T) + noise

    print("原始数据形状:", original_data.shape)
    print("=" * 40, "\n")

    # 2. 初始化并使用PCA模型
    # 我们希望将数据从3维降到2维
    n_components = 2
    pca_model = PCAModel(n_components=n_components)

    # 训练模型并转换数据
    transformed_data = pca_model.fit_transform(original_data)

    print(f"\n将数据从3维降至{n_components}维。")
    print("降维后数据形状:", transformed_data.shape)

    # 3. 查看结果
    print("\n每个主成分的方差贡献率:", pca_model.explained_variance_ratio_)
    print(f"前 {n_components} 个主成分累计方差贡献率: {np.sum(pca_model.explained_variance_ratio_):.4f}")

    # 4. 可视化结果
    fig = plt.figure(figsize=(12, 6))
    plt.suptitle("PCA 降维示例 (三角形数据)", fontsize=16)

    # 绘制原始数据（3D）
    ax1 = fig.add_subplot(121, projection='3d')
    ax1.scatter(original_data[:, 0], original_data[:, 1], original_data[:, 2], c='b', marker='o', alpha=0.6)
    ax1.set_title("原始数据 (3D)")
    ax1.set_xlabel("特征 1")
    ax1.set_ylabel("特征 2")
    ax1.set_zlabel("特征 3")

    # 绘制降维后的数据（2D）
    ax2 = fig.add_subplot(122)
    ax2.scatter(transformed_data[:, 0], transformed_data[:, 1], c='r', marker='^', alpha=0.6)
    ax2.set_title(f"降维后的数据 ({n_components}D)")
    ax2.set_xlabel("第一主成分")
    ax2.set_ylabel("第二主成分")
    ax2.grid(True)
    ax2.axhline(0, color='grey', lw=0.5)
    ax2.axvline(0, color='grey', lw=0.5)
    ax2.set_aspect('equal', adjustable='box')  # 保持长宽比，让形状更真实

    plt.tight_layout(rect=[0, 0, 1, 0.96])
    plt.show()

UMAP 数据降维

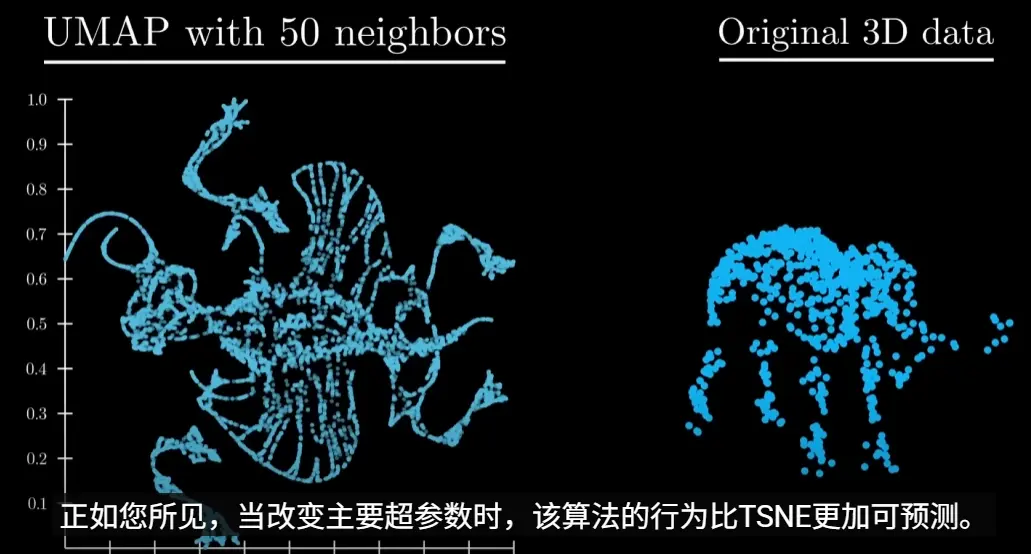
UMAP 是加拿大的Tutte Institute for Mathematics and Computing的Leland研究员于2018年提出的一种对数据非线性降维并可视化的技术，因其出色的可视化质量和计算速度而备受青睐

数据降维适用场景

核心应用场景一：探索性数据分析 (EDA) 与可视化洞察

这是UMAP最强大、最直接的应用场景。当你拿到一份复杂的高维数据时，首要任务就是理解它

目标：
- 快速理解数据的内在结构和分布
- 识别数据中是否存在天然的簇群 (Clusters)
- 发现异常点 (Outliers)
- 为后续的建模方向提供假设和灵感
操作方法：
1. 提取数据的主要特征列
2. 使用UMAP将其降至2维或3维
3. 绘制散点图
4. 关键一步：如果数据有标签（如客户等级、产品类别）或需要预测的目标值（如房价、满意度），用这些值给散点图上色
竞赛价值：一张高质量的UMAP降维图本身就是论文中一个重要的加分项。它可以直观地展示你对数据的深刻理解，并为你后续的模型选择提供强有力的支撑。例如，如果你发现数据清晰地分成了三簇，那么后续采用分段建模或聚类分析就变得顺理成章

核心应用场景二：聚类分析的黄金搭档

在无监督学习问题中，直接在高维数据上进行聚类，效果往往不佳，因为“维度灾难”会使得距离度量失效

目标：
- 提升聚类算法（如K-Means, DBSCAN, 层次聚类）的效果
- 在噪声和无关特征中，提炼出数据最本质的流形结构
操作方法：
1. 预处理：使用UMAP将原始高维特征降到一个适中的维度（不一定是2D/3D，可以是5~20维）
2. 聚类：在降维后的数据上运行聚类算法
3. 验证：可以将聚类结果作为新的标签，在2D/3D的UMAP图上进行可视化，验证聚类效果
竞赛价值：这是一个非常成熟且有效的技术流程。它能帮你找到比直接聚类更有意义、更稳健的分群结果，是解决各类“客户分群”、“用户画像”、“产品定位”等问题的利器

辅助应用场景 (谨慎使用)：作为补充特征增强模型

在构建预测模型时，UMAP也可以扮演一个辅助角色，为模型提供额外的非线性信息

目标：
- 在不牺牲模型可解释性的前提下，可能地提升预测精度
- 帮助线性模型或神经网络等不擅长自动挖掘交叉特征的模型，捕捉到数据的非线性关系
操作方法：
1. 保留所有原始特征
2. 运行UMAP，生成少数几个（如2~5个）UMAP分量
3. 将这些UMAP分量作为新的特征列，追加到原始数据表的末尾
4. 将这个增强后的数据集喂给你的预测模型
竞赛价值：这是一种“锦上添花”的策略。它保留了原始特征，保证了模型的基本可解释性，同时引入了数据结构的宏观信息。虽然对XGBoost这类强悍的树模型提升可能有限，但有时能带来意想不到的微小提升，在定稿阶段可以尝试

不适用场景（严禁使用）：直接替代原始特征用于预测模型

这是初学者最容易犯的错误，尤其是在回归或分类预测问题中

目标（错误地认为）：通过降维来简化预测模型
为什么不可取：
1. 丧失可解释性（致命缺陷）：你的模型输入变成了无法解释的“UMAP分量1”、“UMAP分量2”。你无法在论文中解释“面积”、“卧室数”等具体因素对房价的影响，这在数学建模中是不可接受的
2. 丢失关键预测信息：UMAP为了保持拓扑结构，可能会丢弃对预测目标至关重要的信息。一个特征可能在结构上不重要，但在数值预测上起决定性作用
竞赛建议：在任何需要解释变量与因变量关系的预测问题中，永远不要用UMAP的输出完全替代你的原始特征

核心步骤

1. 构建高维图

目标是捕捉数据在高维空间中的内在拓扑结构，即点与点之间的连接关系和远近亲疏

寻找近邻点 (Nearest Neighbors)

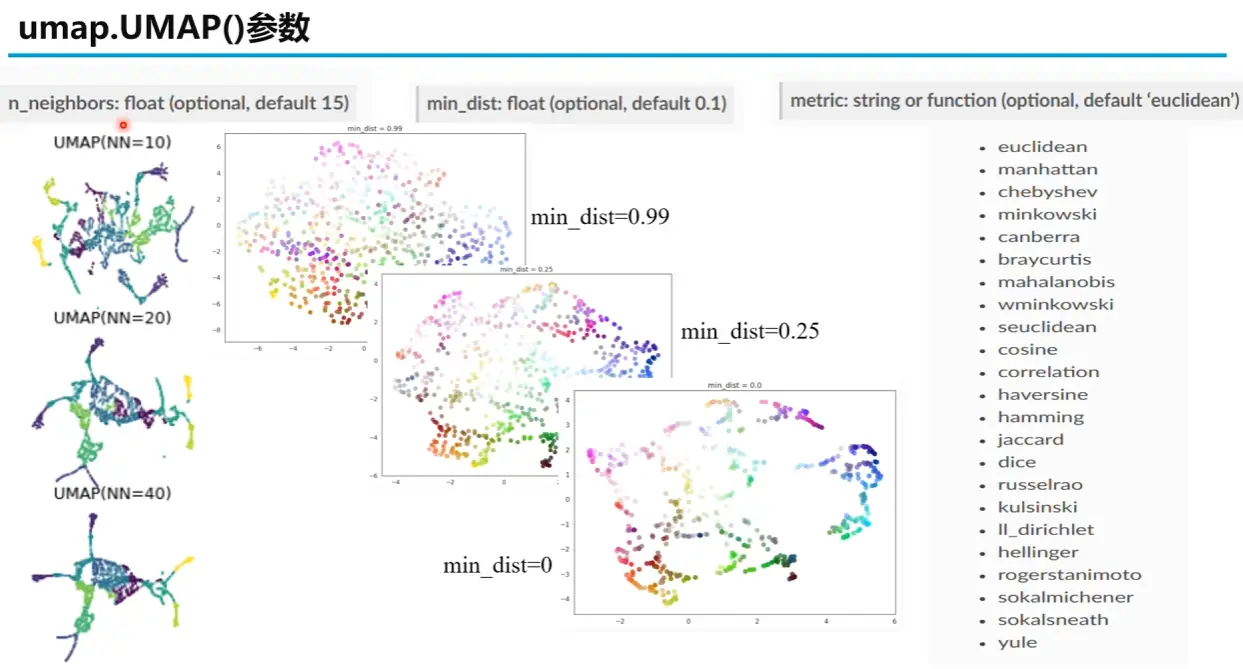
对于数据集中的每一个数据点，UMAP 首先会使用标准的方法（例如 KD-树或 NNDescent）找到它最近的 k 个邻居。这里的 k 是 UMAP 最重要的超参数之一，名为 n_neighbors

n_neighbors 的作用：这个参数决定了 UMAP 在构建图时关注的局部邻域有多大
- 较小的 k 值会使 UMAP 更关注数据的局部结构，可能导致最终的投影图呈现出许多细小的、独立的簇
- 较大的 k 值会迫使 UMAP 考虑更广阔的邻域，从而更好地保留数据的全局结构，但可能会牺牲一些局部细节

为每个点计算局部距离尺度

具体来说，对于每个点 $x_i$ ，UMAP 都会确定一个专属于它的距离尺度 $\sigma_i$ 。对于每一个数据点 $x_i$ ，如果我们使用一个指数衰减函数来计算它与所有其他点 $x_j$ 的连接权重，那么所有这些权重的总和应该等于一个预设的常数，即 $\log_2(k)$

\sum_{j=1}^k \exp\left(-\frac{d(x_i, x_{ij}) - \rho_i}{\sigma_i}\right) = \log_2(k)

在这个公式中：

$x_{ij}$ ：表示点 $x_i$ 的第 $j$ 个最近邻居。求和只在 $x_i$ 的 $k$ 个近邻中进行
$d(x_i, x_{ij})$ ：点 $x_i$ 与其第 $j$ 个近邻之间的原始距离
$\rho_i$ ：点 $x_i$ 到它第一个最近邻居的距离
$\sigma_i$ ：我们要求解的未知数，即点 $x_i$ 独有的局部距离尺度

由于上面的方程很难直接解出 $\sigma_i$ ，UMAP 采用二分查找来求解

最终，每个数据点 $x_i$ 都拥有了一个独一无二的 $\sigma_i$ 值，这个值反映了它所在邻域的数据密度

对于处在数据密集区域的点：它的 k 个近邻距离它非常近。为了让权重总和达到 $\log_2(k)$ ，指数衰减必须非常快，这意味着它需要一个很小的 $\sigma_i$ 。这就像是用一把精密的"小尺子"来测量它和邻居间的细微差别
对于处在数据稀疏区域的点：它的 k 个近邻距离它非常远。为了让权重总和不至于因为距离太大而变得过小，指数衰减必须非常慢，这意味着它需要一个很大的 $\sigma_i$ 。这就像是用一把"大尺子"来连接远方的邻居

计算边权重

其中：

$d(x_i, x_j)$ 是点 $x_i$ 和 $x_j$ 之间的原始距离（如欧氏距离）
$\rho_i$ 是点 $x_i$ 到其第一个最近邻居的距离。设置这个项是为了确保每个点至少和它的最近邻有很强的连接，增加流形的局部连通性
$\sigma_i$ 是上一步计算出的局部距离尺度

然后进行合并

2. 构建低维图

初始化低维表示

UMAP 首先会在目标低维空间中为每个数据点随机（或使用更智能的方法如谱嵌入）生成一个初始位置。我们将这些点记为 $y_1, y_2, \dots, y_n$

计算低维相似度

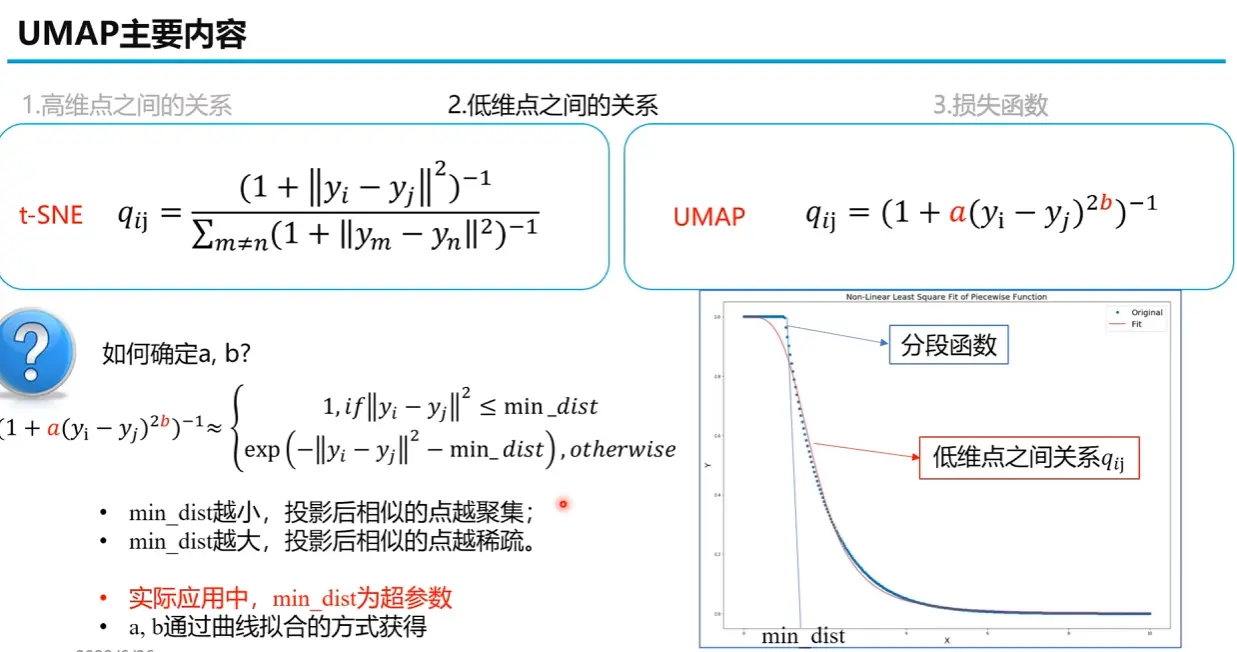
与高维空间类似，我们同样需要在低维空间中计算点与点之间的连接强度 $q_{ij}$ 。UMAP 在这里做了一个简化，它使用了一个预设的、不依赖于数据的曲线族（通常是 t 分布族的变种）来计算相似度

首先，UMAP 根据用户设定的min_dist定义了一个理想的目标关系曲线（蓝色分段曲线），然而，这个分段函数在 min_dist 那个点是不可导的，不方便用于后续的梯度下降优化。因此，UMAP 需要找到一条光滑的、可导的曲线去逼近它。这条光滑曲线就是前面提到的 $q_{ij} = (1 + a(y_i - y_j)^{2b})^{-1}$

算法通过非线性最小二乘法（Non-Linear Least Square Fit），调整 $a$ 和 $b$ 的值，使得红色曲线的形状与蓝色曲线的形状尽可能地接近

3. 构建损失函数 & 迭代优化

UMAP 的目标是让低维的相似度分布 $Q$ 尽可能地匹配高维的相似度分布 $P$ 。它通过一个称为交叉熵 (Cross-Entropy) 的损失函数来衡量这两个分布之间的差异：

\text{Cost} = \sum_{i,j} \left[ P_{ij} \log \left( \frac{P_{ij}}{Q_{ij}} \right) + (1 - P_{ij}) \log \left( \frac{1 - P_{ij}}{1 - Q_{ij}} \right) \right]

这个损失函数由两部分组成：

吸引力项 ( $P_{ij} \log (\ldots)$ )：如果两个点在高维空间中是近邻 ( $P_{ij}$ 较大)，这个项会促使它们在低维空间中也相互靠近（增大 $Q_{ij}$ ）
排斥力项 ( $(1 - P_{ij}) \log (\ldots)$ )：如果两个点在高维空间中不是近邻 ( $P_{ij}$ 较小)，这个项会促使它们在低维空间中相互远离（减小 $Q_{ij}$ ）

UMAP 使用随机梯度下降 (Stochastic Gradient Descent, SGD) 算法来最小化这个损失函数。在每次迭代中，算法会随机取样图中的一条边（一个点对），计算其产生的吸引力和排斥力，然后沿着梯度的方向微调低维空间中这两个点的位置。这个过程会不断重复，直到低维的布局收敛到一个稳定的状态，即损失函数达到最小值

为了提高效率，UMAP 在排斥力计算上使用了负采样 (Negative Sampling) 的优化技巧，即对于每个正样本（相连的边），只采样少数几个负样本（不相连的边）来计算排斥力，而不是计算所有点对之间的排斥力，这极大地提升了算法的速度

最终得到的低维点集 $\{ y_i \}$ 就是 UMAP 的降维结果

超参数

示例代码

# -*- coding: utf-8 -*-
"""
pip install umap-learn scikit-learn matplotlib pandas
"""

import umap
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import warnings

# 设置绘图风格和处理中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
warnings.filterwarnings('ignore')

print(f"UMAP version: {umap.__version__}")

# 这里我们首先用 make_blobs 生成一些模拟数据，以演示UMAP的效果。
# 这些数据在高维空间中有明显的分簇结构。

# 生成模拟数据
# n_samples: 样本数量
# n_features: 每个样本的特征维度（即原始维度）
# centers: 簇的数量
# cluster_std: 簇内数据的离散程度
# random_state: 随机种子，确保每次运行结果一致
data, labels = make_blobs(n_samples=1500, n_features=50, centers=8, cluster_std=2.5, random_state=42)

print(f"原始数据维度: {data.shape}")
print(f"标签数量: {len(np.unique(labels))}")

# **重要步骤**: 数据标准化
# UMAP对数据的尺度敏感，进行标准化处理通常能得到更好的结果。
scaled_data = StandardScaler().fit_transform(data)

# 这是UMAP的核心部分。我们将高维数据降至2维，方便可视化。

print("\n开始进行2D降维...")

# 初始化UMAP模型
# 关键超参数解释 (竞赛中最需要关注和调试的参数):
# n_neighbors: 近邻点数量。控制UMAP如何平衡局部和全局结构。
#              值越小，越关注局部结构，可能把数据分成很多小团。
#              值越大，越关注全局结构，能看到更大范围的关联。
#              通常建议取值范围在 5 到 50 之间。这是最重要的参数！
# min_dist: 控制降维后点与点之间的最小距离。
#           值越小，点簇会越紧密。
#           值越大，点簇会越松散。
#           该参数主要影响可视化效果。
# n_components: 降维后的目标维度。可视化通常设为2或3。
# metric: 计算距离的方式，默认为'euclidean'（欧氏距离），适用于大多数情况。
# random_state: 随机种子，确保结果可复现。

reducer_2d = umap.UMAP(
    n_neighbors=15,
    min_dist=0.1,
    n_components=2,
    metric='euclidean',
    random_state=42
)

# 训练模型并进行降维
embedding_2d = reducer_2d.fit_transform(scaled_data)

print(f"2D降维后数据维度: {embedding_2d.shape}")

#4. 2D结果可视化
print("开始绘制2D降维结果图...")

plt.figure(figsize=(12, 10))
# 使用原始的标签来给降维后的点上色，以验证降维效果
scatter = plt.scatter(
    embedding_2d[:, 0],
    embedding_2d[:, 1],
    c=labels,
    cmap='Spectral',  # 使用光谱色图，视觉效果好
    s=5  # 点的大小
)

plt.title('UMAP 2D 降维结果 (n_neighbors=15, min_dist=0.1)', fontsize=16)
plt.xlabel('UMAP Component 1', fontsize=12)
plt.ylabel('UMAP Component 2', fontsize=12)
plt.gca().set_aspect('equal', 'datalim')

# 添加颜色图例
legend1 = plt.legend(handles=scatter.legend_elements()[0],
                     labels=[f'Cluster {i}' for i in range(len(np.unique(labels)))],
                     title="数据簇")
plt.gca().add_artist(legend1)
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()

# **结果解读**:
# 如果UMAP运行良好，您应该能看到图中相同颜色的点聚集在一起，形成了清晰的簇。
# 这说明UMAP成功地在高维空间中找到了数据的内在结构，并将其呈现在了2D平面上。


# 5. UMAP模型训练与3D降维及可视化
# 有时3D可视化能提供比2D更丰富的信息。

print("\n开始进行3D降维...")

# 将 n_components 设为 3
reducer_3d = umap.UMAP(
    n_neighbors=15,
    min_dist=0.1,
    n_components=3,
    metric='euclidean',
    random_state=42
)

embedding_3d = reducer_3d.fit_transform(scaled_data)
print(f"3D降维后数据维度: {embedding_3d.shape}")

# 绘制3D散点图
print("开始绘制3D降维结果图...")
fig = plt.figure(figsize=(14, 12))
ax = fig.add_subplot(111, projection='3d')

ax.scatter(
    embedding_3d[:, 0],
    embedding_3d[:, 1],
    embedding_3d[:, 2],
    c=labels,
    cmap='Spectral',
    s=5
)

ax.set_title('UMAP 3D 降维结果', fontsize=16)
ax.set_xlabel('UMAP Component 1', fontsize=12)
ax.set_ylabel('UMAP Component 2', fontsize=12)
ax.set_zlabel('UMAP Component 3', fontsize=12)
plt.show()

DEA 数据包络分析

I. 一种用于绩效评估的非参数前沿方法

A. 定义相对效率与标杆管理

数据包络分析（Data Envelopment Analysis, DEA）是一种源于运筹学和经济学的实证性、非参数化方法，其核心目标是评估一组同质实体（称为决策单元，Decision Making Units, DMU）的相对生产效率。在本质上，DEA是一种标杆管理（Benchmarking）工具，它通过比较每个DMU的多种投入（Inputs）与多种产出（Outputs）的组合，来衡量其绩效表现。效率的基本概念被定义为所有加权产出的总和与所有加权投入的总和之比。

DEA的应用范围极其广泛，已成功渗透到国际银行业、医疗健康服务、教育评估、警务运营、物流管理乃至经济可持续性研究等多个领域。近年来，其应用甚至扩展到了评估自然语言处理模型的性能，并在机器学习领域展现出巨大的潜力。

与传统的绩效评估方法不同，DEA并不试图构建一个普适的、严格意义上的“生产函数”，而是旨在从实践数据中识别出最高效的运营模式。这一特性使其成为一个极具实践价值的管理工具。

B. 思想溯源：从法雷尔前沿到CCR模型

DEA的智力谱系可以追溯到经济学家迈克尔·詹姆斯·法雷尔（Michael James Farrell）于1957年发表的开创性论文《生产效率的衡量》。法雷尔提出了一个革命性的思想：用“非预设的生产函数”来估算效率，即通过对观测数据进行分段线性包络来构建效率前沿，而非事先假定一个特定的函数形式（如Cobb-Douglas函数）。法雷尔的另一个关键贡献在于，他将整体效率分解为两个核心部分：

技术效率（Technical Efficiency）：衡量在维持产出不变的情况下，投入能够被按比例缩减的程度，即消除资源浪费的能力。
配置效率（Allocative Efficiency）：也称价格效率，衡量在给定投入品价格下，企业是否使用了成本最低的投入组合。

尽管法雷尔的理论极具洞察力，但在随后的二十年里，它在很大程度上被学术界所忽视，部分原因在于其计算的复杂性，尤其是在处理多产出问题时。

真正的突破发生在1978年，亚伯拉罕·查恩斯（Abraham Charnes）、威廉·W·库珀（William W. Cooper）和爱德华多·罗德斯（Edwardo Rhodes）发表了题为《衡量决策单元的效率》的里程碑式论文。这篇论文被公认为DEA领域的奠基之作，其引用次数超过700次（截至1999年）并持续增长。有趣的是，这一突破的催化剂是库珀的博士生罗德斯，他将法雷尔那篇沉寂了二十年的论文带到了导师的视野中。查恩斯、库珀和罗德斯（Charnes, Cooper, and Rhodes，简称CCR）巧妙地运用线性规划（Linear Programming）方法，将法雷尔的思想操作化，使其能够轻松处理多投入、多产出的复杂情况，并正式将这一方法命名为“数据包络分析”。

CCR模型的诞生并非纯粹的理论推演，而是为了解决一个棘手的现实问题。当时，罗德斯的博士论文正聚焦于评估一项名为“贯彻项目”（Program Follow Through）的美国联邦政府计划，该计划旨在帮助弱势儿童。这个项目的投入和产出极为复杂且难以用货币衡量，例如投入包括“母亲陪伴孩子阅读的时间”，产出则包括“提升弱势儿童的自尊心”等。传统的经济学或统计学方法在面对这类异质性、非公度和缺乏市场价格的变量时显得力不从心。CCR模型通过线性规划为每个DMU寻找一组“最有利”的权重，从而在无需预设价格或函数形式的前提下评估效率，完美地解决了这一难题。这揭示了DEA一个最核心且持久的优势：它能够在投入产出指标异质、无法通约且缺乏市场价格的复杂场景下进行有效的绩效评估，这在公共部门和非营利组织的评估中尤为常见。

C. 为何选择非参数方法

DEA之所以被广泛采用，其非参数特性是根本原因。与参数化方法（如回归分析或随机前沿分析SFA）相比，DEA的优势体现在以下几个方面。

首先，参数化方法要求研究者必须预先设定一个具体的生产或成本函数形式。这一假设具有很强的主观性，如果设定的函数形式与真实的生产过程不符，将会导致评估结果产生系统性偏差。DEA则完全避免了这个问题，它不依赖任何函数形式的假设，而是直接从观测数据中构建“最佳实践前沿”。

其次，DEA的核心优势在于其处理多维投入和产出的能力。传统的绩效评估方法，如财务比率分析，在面对多个指标时常常会给出相互矛盾的信号，而DEA能够将这些多维度的指标整合进一个统一的效率框架中进行综合评估。

最后，尽管DEA解决的是一个比率优化问题，但通过数学变换，它可以被转换成一个标准的线性规划问题，使得计算变得非常简便和高效。

总结而言，DEA之所以广受欢迎，主要基于三个原因：

假设条件相对较少：无需预设生产函数，减少了主观偏误的风险。
能够处理多维投入产出：可以对复杂的运营系统进行全面的标杆比较。
计算简便：可以通过线性规划直接求解效率比率。

II. DEA的架构支柱

A. 决策单元（DMU）

决策单元（Decision Making Unit, DMU）是DEA分析的基本评估对象。理论上，任何一个能够将投入转化为产出的同质实体，都可以被视为一个DMU。DEA的强大之处在于其评估对象的广泛适应性，这些DMU可以是：

商业机构：如银行分行、连锁商店、制造工厂、酒店。
公共服务部门：如医院、学校、警察局、法院。
宏观经济单位：如城市、地区甚至国家。

进行DEA分析的一个关键前提是DMU的同质性（Homogeneity）。这意味着所有参与评估的DMU必须执行相似的任务，运作于相似的市场或监管环境中，并使用相同类型的投入来产生相同类型的产出。例如，将一家教学医院与一家社区诊所进行比较是没有意义的，因为它们的目标、资源和产出截然不同。确保同质性是保证DEA结果有效和可比的基础。

B. 投入与产出：效率的构建模块

投入和产出是构建DEA模型的基石。

投入（Inputs）：指DMU在生产过程中所消耗或利用的各种资源。这些可以是人力资源（如员工数量、工时）、资本（如设备数量、资产总额）、物料或其他运营成本（如运营费用、能源消耗）。
产出（Outputs）：指DMU通过转化投入所产生的产品或服务。这些可以是实体产品（如产品数量）、服务量（如服务的客户数、处理的交易笔数）或财务结果（如收入、利润）。

DEA的一个显著特点是它能够同时处理多个投入和多个产出，并且这些指标的计量单位可以完全不同。例如，一个零售店的DEA模型可以同时包含以“人数”计量的员工数量、以“平方米”计量的店铺面积、以“美元”计量的运营费用作为投入，以及以“件数”计量的销售量和以“美元”计量的利润作为产出。这与传统的比率分析形成了鲜明对比，后者在处理多个比率（如人均销售额、坪效）可能出现的矛盾信号时会遇到困难。

指标的选择对DEA结果至关重要。选择的投入和产出指标应能逻辑清晰地代表被评估的生产过程。分析师面临的挑战是构建一个“精简”（parsimonious）的模型：既要包含足够多的变量以全面反映DMU的运作，又要尽可能少以保持模型的判别力。

C. 效率前沿：包络最佳实践

效率前沿（Efficiency Frontier），也称为生产前沿或最佳实践前沿，是DEA的核心概念。与理论经济学中抽象的生产函数不同，DEA的效率前沿是经验性的，它完全由样本数据中表现最佳的DMU所构成。

“数据包络分析”这个名称的由来，正是因为它构建的效率前沿面像一个“信封”一样，将所有的数据点“包络”在内。位于这个“信封”表面（即前沿面上）的DMU被定义为相对有效（或称DEA有效），其效率得分为1（或100%）。而所有位于“信封”内部的DMU则被视为相对无效，它们的效率通过其与前沿面的距离来衡量。

我们可以通过一个简单的图形来直观理解。假设我们评估一组DMU，每个DMU使用一种投入（Input X）生产一种产出（Output Y）。将所有DMU的数据点绘制在二维坐标系中，DEA会构建一条连接“最高效”数据点的分段线性曲线（或在高维空间中的超平面）。这条曲线就是效率前沿。任何位于曲线下方的点都是无效率的，其无效率的程度可以通过它向曲线上投影的距离来度量。

这种构建方式揭示了DEA的一个深刻内涵：效率前沿代表的是一种“实践中的最优”，而非“理论上的完美”。这对于管理实践具有重要意义。传统经济学理论中的生产函数代表了在现有技术水平下可能达到的绝对最大产出，这是一个无法观测的、理想化的概念。DEA则放弃了对这一理论最优的估计，转而从实际数据中寻找“榜样”。这意味着，一个效率得分为1的DMU并非绝对意义上的“完美”，它只是在当前被评估的样本中表现最好的一个。它是“最佳实践”，而非“完美实践”。

这一特性带来了两个重要的实践推论。第一，DEA的效率评分对样本选择高度敏感。如果向数据集中加入一个新的、效率极高的DMU，它可能会重新定义效率前沿，从而降低其他所有DMU的相对效率得分。第二，它使得DEA成为一个非常务实的管理工具。对于一家效率低下的医院来说，它的改进标杆不再是一个抽象的理论模型，而是一家（或几家）真实存在的、用相似资源取得了更好成果的同行医院。这种“相对且可实现”的标杆特性，正是DEA作为标杆管理和持续改进工具的强大之处。它为管理者提供了具体的、现实世界中的学习榜样，而不是一个遥不可及的理论目标。

III. 基础数学模型：CCR与BCC

DEA方法论建立在两个 foundational 模型之上：CCR模型和BCC模型。它们代表了对生产技术不同假设的理解，并共同构成了现代效率分析的基石。

A. CCR模型：固定规模报酬（CRS）

CCR模型由Charnes、Cooper和Rhodes于1978年提出，是DEA的第一个也是最基础的模型。该模型的核心假设是

固定规模报酬（Constant Returns to Scale, CRS）。CRS假设意味着投入和产出之间存在线性的、成比例的关系，即如果所有投入都增加一倍，所有产出也应该相应地增加一倍。这个假设在所有DMU都被认为在最优规模下运营时是合适的，例如在一个完全竞争的市场中。

CCR模型衡量的效率被称为总技术效率（Overall Technical Efficiency, OTE），它是一个综合性指标，同时包含了纯技术效率和规模效率两个方面。换言之，如果一个DMU在CCR模型下是无效率的，其原因可能是管理不善（技术无效率），也可能是运营规模不当（规模无效率），或者两者兼而有之。只有当一个DMU同时达到技术有效和规模有效时，其CCR效率值才为1。

从数学上看，CCR模型最初被表述为一个分式规划问题，其目标是为待评估的DMU找到一组最优的投入和产出权重（vi和ur），以最大化其效率比率h0，同时保证使用这组权重时，所有其他DMU的效率比率都不超过1。

B. BCC模型：可变规模报酬（VRS）

1984年，Banker、Charnes和Cooper对CCR模型进行了重要扩展，提出了BCC模型。BCC模型放宽了严格的CRS假设，允许

可变规模报酬（Variable Returns to Scale, VRS）的存在。VRS假设更加贴近现实，因为它承认在不完全竞争、政府管制或金融约束等现实因素的影响下，DMU未必能在最优规模上运营。在VRS下，生产过程可能经历规模报酬递增（Increasing Returns to Scale, IRS）、**固定规模报酬（CRS）和规模报酬递减（Decreasing Returns to Scale, DRS）**三个阶段。

C. 效率分解：技术效率与规模效率

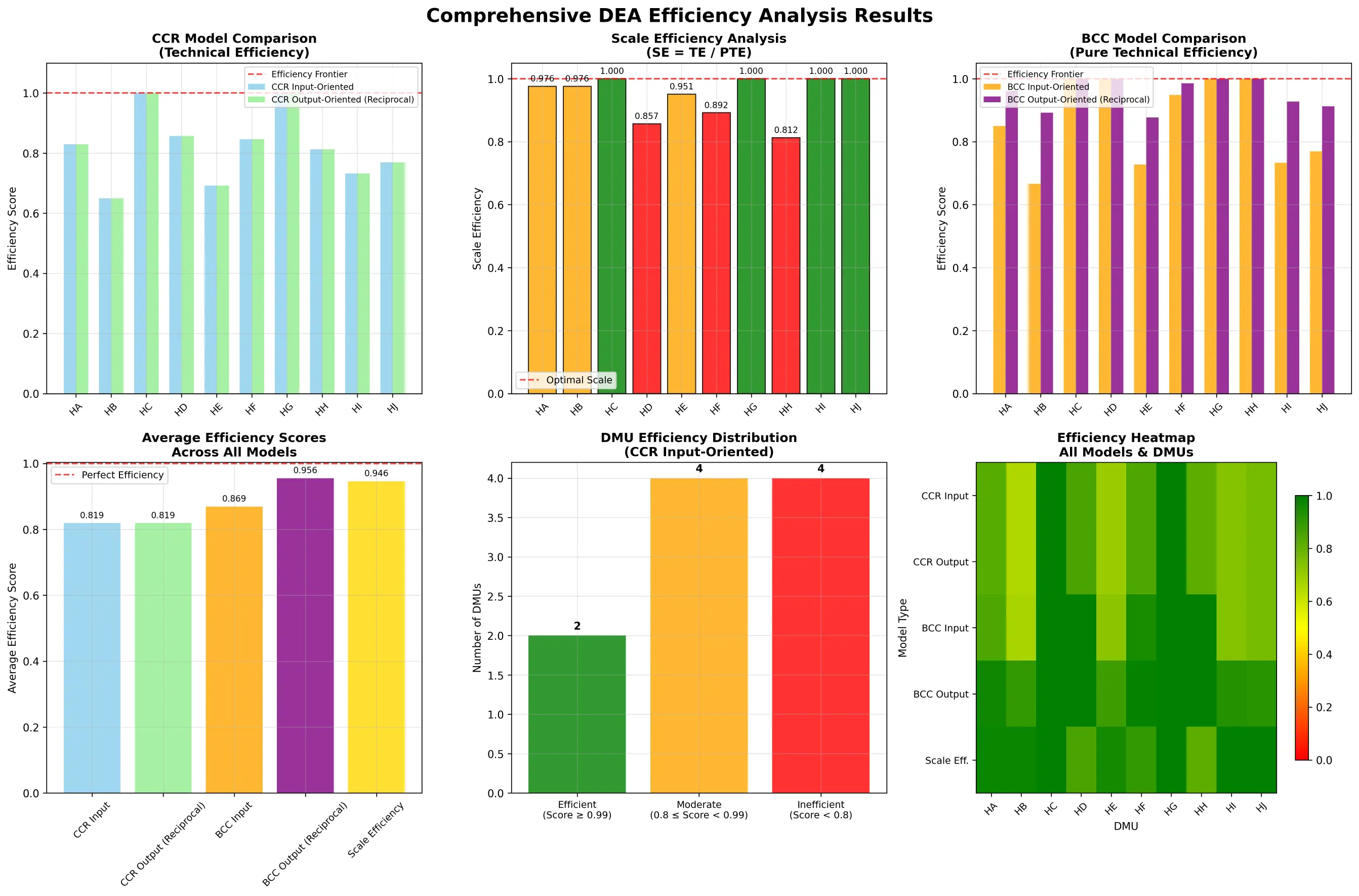
BCC模型最重要的贡献在于它能够将总技术效率（OTE）分解为两个独立的组成部分：纯技术效率（Pure Technical Efficiency, PTE）和规模效率（Scale Efficiency, SE）。

纯技术效率（PTE）：由BCC模型直接测算得出。它衡量的是在排除了规模因素影响后，DMU的管理和运营能力，即在现有规模下，将投入转化为产出的纯粹能力。PTE反映了DMU的资源配置能力和使用效率。
规模效率（SE）：衡量DMU的运营规模是否接近“最优生产规模”。它不能直接从某个模型中得到，而是通过CCR和BCC模型的效率值计算得出：

SE = \frac{OTE_{CCR}}{PTE_{BCC}}

其中， $OTE_{CCR}$ 是CCR模型的效率值， $PTE_{BCC}$ 是BCC模型的效率值。由于 $PTE_{BCC}$ 总是大于或等于 $OTE_{CCR}$ ，因此SE的取值范围在0和1之间。当SE=1时，表示DMU处于最优规模；当SE<1时，表示存在规模无效率。

这种效率分解将DEA从一个简单的效率测量工具，转变为一个强大的管理诊断工具。CCR模型给出的总效率（OTE）回答了“DMU是否有效率？”的问题，而效率分解则进一步回答了“如果无效率，原因何在？”。例如，两家医院可能具有相同的低OTE得分（如0.8），但其背后的原因可能完全不同：

医院A：PTE = 1.0，SE = 0.8。这意味着该医院的管理水平是顶尖的（纯技术有效），但其运营规模过小或过大，导致了规模无效率。其战略改进方向应聚焦于调整规模，如扩张或合并。
医院B：PTE = 0.8，SE = 1.0。这意味着该医院的运营规模是最佳的，但其管理水平存在问题，导致了纯技术无效率。其战略改进方向应是优化内部流程、提升管理能力，而非改变规模。

此外，BCC模型还能进一步判断规模无效率的类型。通过分析对偶问题中的变量，可以确定DMU处于规模报酬递增（IRS）还是递减（DRS）阶段。

IRS：表示DMU规模偏小，扩大规模可以带来更高的投入产出效率。
DRS：表示DMU规模偏大，可能出现了管理拥堵或范围不经济，缩减规模反而能提升效率。

这种从“是否有效”到“为何无效”以及“如何改进”的分析深化，是BCC模型的核心价值所在，它为管理者提供了具体、可操作的战略建议。

表1：CCR与BCC模型对比

特征	CCR 模型 (Charnes, Cooper, Rhodes, 1978)	BCC 模型 (Banker, Charnes, Cooper, 1984)
全称	Charnes-Cooper-Rhodes 模型	Banker-Charnes-Cooper 模型
核心假设（规模报酬）	固定规模报酬 (Constant Returns to Scale, CRS)	可变规模报酬 (Variable Returns to Scale, VRS)
衡量的效率	总技术效率 (Overall Technical Efficiency, OTE)，包含技术和规模效率	纯技术效率 (Pure Technical Efficiency, PTE)，剔除了规模影响
新增数学约束	无（相对于BCC）	在对偶（包络）形式中增加凸性约束 (∑λj=1)
效率值解读	反映了管理水平和运营规模的综合效率	仅反映在当前规模下的管理和运营效率
主要应用场景	适用于所有DMU被认为在最优规模下运营的理想情况	适用于存在不完全竞争、管制等导致DMU规模各异的现实情况
提供的战略洞察	识别整体效率低下的DMU	将无效率分解为技术层面和规模层面，提供更精确的诊断和改进方向

IV. 战略导向：投入最小化与产出最大化

在构建DEA模型时，分析师必须做出一个关键的战略选择：采用**投入导向（Input-Oriented）模型还是产出导向（Output-Oriented）**模型。这个选择并非技术上的细枝末节，而是深刻反映了被评估DMU的战略姿态及其所处的运营环境。

A. 投入导向模型

投入导向模型旨在回答这样一个问题：“在保持当前产出水平不变的情况下，各项投入可以按比例减少多少？”。这种模型的关注点是投入的节约和成本的控制。

它特别适用于管理者对投入拥有较大控制权，而对产出控制权较小的场景。公共服务部门是典型的例子。例如，一所公立学校或一家公立医院，其服务对象数量（产出）往往由政府或社会需求决定，是相对固定的；而其预算、人员配置和资源使用（投入）则是管理者可以进行优化的方面。因此，在评估这类以成本控制和资源有效利用为核心目标的组织时，投入导向模型是自然的选择。其数学目标是最小化一个表示投入缩减比例的标量 $\theta$ （其中 $\theta \le 1$ ）。

B. 产出导向模型

与投入导向模型相反，产出导向模型旨在回答：“在保持当前投入水平不变的情况下，各项产出可以按比例增加多少？”。这种模型的关注点是产出的扩张和收益的最大化。

它适用于管理者对投入控制权较小（例如，预算或资源在短期内是固定的），而对产出有较大影响力的场景。一个典型的例子是追求市场份额和销售增长的私营企业。在给定的工厂规模、员工数量和资本投入下，企业的目标是最大化其产品产量和销售收入。因此，在评估这类以增长和市场扩张为核心目标的组织时，产出导向模型更为合适。其数学目标是最大化一个表示产出扩张比例的标量 $\phi$ （其中 $\phi \ge 1$ ）。

C. 等价性与差异性

投入导向和产出导向模型的选择，其结果会受到规模报酬假设的影响。

在固定规模报酬（CRS）假设下：投入导向和产出导向模型是等价的。它们会识别出完全相同的效率前沿和相同的有效DMU集合。一个DMU的投入效率值（θ）和产出效率值（ϕ）互为倒数，即 $\theta = 1/\phi$ 。因此，在CRS假设下，模型导向的选择不会影响最终的效率排序。
在可变规模报酬（VRS）假设下：情况则有所不同。虽然两种导向仍然会识别出相同的有效DMU集合（效率值为1的单位），但对于无效率的DMU，它们的效率得分（θ和 $\phi$ ）不再是简单的倒数关系，并且它们在前沿面上的投影点（即改进目标）也可能不同。

这个选择的背后，体现了组织的战略优先级。一个采用投入导向模型的组织，其隐含的战略姿态是防御性的、内向的，聚焦于在现有市场或约束下通过降本增效来提升竞争力。而一个采用产出导向模型的组织，其战略姿态则是进攻性的、外向的，聚焦于在现有资源基础上通过扩大产出来抢占市场和市场和实现增长。因此，分析师在选择模型导向时，必须深入理解被评估DMU的业务性质、市场环境和战略意图，以确保DEA模型给出的“改进建议”是符合其实际情况和目标的。

表2：投入导向与产出导向模型的战略指南

标准	投入导向模型	产出导向模型
核心问题	在产出不变的情况下，投入能减少多少？	在投入不变的情况下，产出能增加多少？
管理焦点	成本控制、资源节约、效率提升	产出扩张、收入增长、市场份额
战略姿态	防御性、内向型、整合优化	进攻性、外向型、增长扩张
典型应用场景（公共部门/成本中心）	公立医院、公立学校、政府机构等，其服务目标（产出）固定，需最小化成本（投入）	较少见，除非目标是最大化服务覆盖范围
典型应用场景（私营部门/利润中心）	处于成熟或饱和市场，以降本为主要竞争手段的企业	处于成长型市场，以扩大生产和销售为主要目标的企业
数学目标	最小化投入缩减因子 θ	最大化产出扩张因子 ϕ
得分解释（以无效率DMU为例）	$\theta < 1$ ，表示为达到有效所需达到的投入水平占当前投入的比例	$\phi > 1$ ，表示为达到有效所需达到的产出水平是当前产出的倍数

V. 从数据到决策：为可操作洞察解读DEA结果

DEA分析的最终目的不是生成一堆数字，而是为管理决策提供清晰、可操作的洞察。要实现这一目标，必须对DEA的各项输出结果进行深入解读。

A. 效率分值（θ）

效率分值（通常用 $\theta$ 表示）是DEA模型最直接的输出，其取值范围为(0, 1]。这个分数代表了DMU的相对效率水平。

效率分值为1：表示该DMU是相对有效的，位于由样本数据构成的效率前沿面上。这意味着，在当前样本中，没有其他任何一个DMU或DMU的线性组合能用更少的投入产生同样多的产出（或用同样的投入产生更多的产出）。
效率分值小于1：表示该DMU是相对无效的。分值越低，无效率的程度越高。例如，一个投入导向模型中效率为0.8的DMU，意味着它只需使用当前80%的投入，就可以维持现有的产出水平。

需要注意的是，效率值为1的DMU之间还存在进一步的区分：

强有效（Strongly Efficient）：不仅效率值为1，而且其所有的投入和产出松弛变量（见下文）均为零。这代表了真正的最佳实践。
弱有效（Weakly Efficient）：效率值为1，但至少存在一个非零的松弛变量。这意味着该DMU虽然在径向改进上已经达到最优，但在某些特定投入或产出上仍有“非径向”的改进空间（例如，某个投入过多或某个产出不足）。

B. 发现浪费：投入/产出松弛量（Slack Variables）

对于效率值小于1的无效率DMU，仅仅知道其效率分数是不够的。松弛变量提供了关于资源浪费或产出不足的更具体、更精细的信息。

投入冗余（Input Slacks, $s^-$ ）：表示在按比例缩减所有投入（由效率值 $\theta$ 决定）之后，某些特定投入额外需要减少的数量，才能使该DMU达到前沿水平。例如，一个效率为0.9的医院，除了需要将所有投入（医生、护士、床位）都减少10%之外，其投入松弛变量可能显示，行政人员数量还需要额外再减少5人。这指出了非均衡的资源浪费。
产出不足（Output Slacks, $s^+$ ）：表示在按比例增加所有产出之后，某些特定产出额外需要增加的数量。例如，一家银行分行在达到其径向产出目标后，其产出松弛变量可能显示，其理财产品销售额还需要额外再增加10万美元。

松弛变量是DEA提供可操作建议的关键。它将分析从“你需要整体上节约10%的成本”深化到“你需要在整体节约10%成本的基础上，重点削减X部门的Y项开支”，从而为管理者提供了精确的改进靶点。

C. 参照集（Peer Group）的角色

对于每一个无效率的DMU，DEA分析都会识别出一个或多个有效的DMU作为其参照集，也称为对等组（Peer Group）。

这个参照集由那些构成效率前沿特定“面”的有效DMU组成，无效率的DMU正是向这个“面”进行投影以计算其效率。从数学上讲，无效率DMU的改进目标（即其在前沿面上的投影点）可以表示为参照集中各个有效DMU的投入产出向量的加权平均（凸组合），权重即为 $\lambda$ 值。

参照集的作用超越了纯粹的数学计算，它是连接定量分析与定性管理改进的桥梁。它为无效率的DMU提供了具体的、现实世界中的学习榜样和标杆。一个无效率的DMU的管理者不再面对一个抽象的“100分”目标，而是可以清晰地看到：“医院A”和“医院B”就是我的参照集，它们用和我相似的资源取得了比我更好的成果。

接下来的管理任务就变得非常明确：深入研究参照集中的同行。它们采用了什么样的运营流程？使用了何种技术？它们的组织架构和激励机制是怎样的？通过对这些“最佳实践者”的深入剖-析，无效率的DMU可以找到适合自身的、切实可行的改进路径。

因此，可以说参照集是DEA分析对实践管理者而言最有价值的输出之一。它将抽象的效率分数转化为一个具体的学习对象列表，将标杆管理的理念操作化，有效地将模型的数学优化与组织的学习和适应过程联系起来。

VI. 衡量动态生产率：Malmquist指数

当分析涉及跨越多个时间段的面板数据时，静态的DEA模型虽然可以在每个时期独立评估效率，但却无法捕捉生产率的动态变化。为了解决这个问题，Caves, Christensen和Diewert在1982年提出了Malmquist指数，它与DEA方法相结合，成为衡量跨时期生产率变化（Total Factor Productivity, TFP）的强大工具。

Malmquist指数的核心思想是，通过计算一个DMU在两个不同时间点（例如t和t+1）相对于技术前沿的距离比率，来衡量其生产率的变化。基于DEA的Malmquist指数通过构建不同时期的效率前沿，并将一个时期的DMU与另一个时期的前沿进行比较，从而实现对生产率变化的测度。

A. Malmquist指数的分解

Malmquist指数最吸引人的地方在于，它可以被分解为两个核心组成部分，从而为生产率变化的来源提供深刻的洞察：

技术效率变化（Efficiency Change, EC）：也称为“追赶效应”（Catch-up Effect）。它衡量的是一个DMU自身相对于其所处时代的技术前沿的效率变化。换句话说，它回答了这样一个问题：“这个DMU在追赶其所在时代的最佳实践方面，是进步了还是退步了？”
- EC > 1：表示技术效率有所改善，DMU正在向其时代的生产前沿靠近。
- EC < 1：表示技术效率出现恶化，DMU正在远离其时代的生产前沿。
- EC = 1：表示技术效率没有变化。
技术进步（Technical Change, TC）：也称为“前沿移动效应”（Frontier-shift Effect）。它衡量的是技术前沿本身在两个时期之间的移动。这通常反映了由技术创新、管理范式革新或宏观环境改善带来的整个行业的进步。它回答了这样一个问题：“整个行业的技术水平是进步了还是退步了？”
- TC > 1：表示技术前沿向外扩张，即发生了技术进步。这意味着在相同的投入水平下，可以获得更多的产出。
- TC < 1：表示技术前沿向内收缩，即发生了技术退步。这在某些情况下可能发生，例如由于新的、更严格的环境法规导致生产可能性下降。
- TC = 1：表示技术前沿没有移动。

总的全要素生产率变化（TFPCH）由这两个部分相乘得到：

TFPCH (Malmquist Index) = EC × TC

B. 解读Malmquist指数

通过对Malmquist指数的分解，管理者可以获得比单一生产率数字更丰富的信息，从而进行更精确的诊断：

TFPCH > 1：表示DMU的全要素生产率在两个时期之间有所增长。
TFPCH < 1：表示DMU的全要素生产率出现了下降。
TFPCH = 1：表示DMU的全要素生产率没有变化。

更重要的是，我们可以分析生产率变化的驱动因素。例如，两个DMU可能都有相同的TFPCH值（如1.05，表示5%的增长），但其背后的故事可能完全不同：

DMU A: EC = 1.10, TC = 0.95。这意味着该DMU通过改善内部管理和运营，实现了10%的效率提升（追赶效应），但整个行业的技术水平实际上是退步了5%。该DMU的增长是内生性的，它在逆境中实现了超越。
DMU B: EC = 0.95, TC = 1.10。这意味着该DMU虽然享受了整个行业技术进步带来的10%的红利，但其自身的管理效率实际上是下降了5%。该DMU的增长是外生性的，它未能跟上技术进步的步伐，甚至出现了管理滑坡。

这种分解使得管理者能够清晰地辨别，绩效的改善或恶化究竟是源于自身的努力，还是仅仅搭了行业发展的“顺风车”（或成为行业衰退的受害者）。

C. 应用与局限

Malmquist指数在各种领域都有广泛应用，例如评估银行、医院、制造企业、甚至国家在不同年份的生产率变化。

然而，它也有一些需要注意的局DENOUNCED。例如，在存在非固定规模报酬的情况下，传统的Malmquist指数可能无法准确地衡量生产率的变化。此外，计算指数有不同的方法（如基于相邻时期或固定基期），这些选择可能会影响结果。

尽管如此，Malmquist指数作为DEA框架的一个重要动态扩展，为理解和分析跨时期绩效演变提供了一个强大而富有洞察力的分析工具。

VII. 前沿拓展：扩展DEA框架

基础的CCR和BCC模型虽然强大，但在处理更复杂的现实问题时存在局限性。为了克服这些不足，DEA领域发展出了一系列高级模型，极大地扩展了其分析能力和应用范围。

A. 对“最佳”进行排序：超效率模型

问题：标准DEA模型的一个显著缺点是，所有位于效率前沿上的DMU都被赋予相同的效率值“1”，这使得我们无法对这些“最佳实践者”进行进一步的区分和排序。在资源分配或评奖等场景下，这显然是一个问题。

解决方案：为了解决这个问题，Andersen和Petersen在1993年提出了超效率（Super-efficiency）DEA模型。其核心思想非常巧妙：在评估某一个DMU的效率时，暂时将其从参照集中移除，然后用剩余的DMU构建效率前沿来评估它。

对于一个原本无效率的DMU，其效率值与标准模型相同。
对于一个原本有效率的DMU，由于它现在位于由其“次优”同行构建的前沿之外，其效率得分将可以大于1。

解读：超效率得分提供了一个对有效DMU进行排序的依据。得分越高，表示该DMU的效率水平越“稳固”。这个得分也可以被解读为一种稳定性或鲁棒性的度量：在一个投入导向的模型中，一个超效率得分为1.2的DMU意味着，即使它的所有投入都增加20%，它相对于其他DMU而言仍然是有效的。这为决策者识别“最佳中的最佳”提供了有力的工具。

注意事项：需要指出的是，超效率模型在某些情况下可能无解（infeasible），尤其是在可变规模报酬（VRS）假设下，当被评估DMU的投入产出组合无法被其他DMU的组合所包络时。

B. 打开“黑箱”：用于多阶段过程的网络DEA

问题：传统DEA模型将DMU视为一个“黑箱”，只关心最终的投入和产出，而忽略了其内部复杂的运作流程和子单元之间的相互作用。这导致我们无法定位组织内部效率瓶颈的具体环节。

解决方案：**网络DEA（Network DEA）模型通过将DMU的内部结构建模为一系列相互连接的子流程或阶段，从而打开了这个“黑箱”。这些阶段通过

中间产品（Intermediate Products）**联系起来——一个阶段的产出成为下一个阶段的投入。

应用范例（银行业）：网络DEA在银行业评估中得到了广泛应用，一个经典模型是两阶段银行效率模型：

第一阶段：运营效率（或存款吸收效率）。此阶段关注银行如何利用其物理和人力资源（如员工、固定资产）来吸收资金。
- 投入：员工人数、运营成本、固定资产。
- 中间产出：吸收的存款总额、其他负债。
第二阶段：盈利效率（或资产运用效率）。此阶段关注银行如何将吸收来的资金（中间产品）转化为收益。
- 中间投入：第一阶段产生的存款总额。
- 最终产出：贷款总额、投资收益、利息收入、利润。

通过网络DEA，分析师不仅可以得到银行的总体效率，还能分别计算出其运营效率和盈利效率。这使得诊断可以更加精确：一家银行的整体效率低下，究竟是因为它吸收存款的成本过高（第一阶段无效率），还是因为它未能有效地将这些存款转化为高收益资产（第二阶段无效率）？这种精细化的诊断为管理改进提供了更明确的方向。

C. 捕捉时间维度：用于面板数据分析的动态DEA

问题：当拥有跨越多个时期的数据（即面板数据）时，使用静态DEA模型在每个时期独立进行分析会忽略时期之间的内在联系，可能导致误导性的结论。例如，本年度的资本投资（投入）可能会在未来几年才产生效益（产出）。

解决方案：**动态DEA（Dynamic DEA）模型通过引入结转变量（Carry-over Variables）**来明确地连接连续的时间周期。结转变量代表了那些可以从一个时期“携带”到下一个时期的因素，它们可以是：

期望的（Desirable）：如固定资产、研发投入、留存收益、知识存量。
不期望的（Undesirable）：如坏账、累积的污染物。
自由的（Free）：可由管理者自行决定的。
固定的（Fixed）：管理者无法控制的。

解读：动态DEA不仅评估每个时期的效率，还评估整个考察期内的系统总效率。它揭示了系统总效率与各时期效率之间的数学关系——系统总效率的补数是各时期效率补数的线性组合。这种方法能够更准确地描绘DMU的长期绩效演变轨迹，并评估其资源跨期配置的有效性。

D. 考虑外部性：包含非期望产出的模型

问题：许多生产过程在产生期望产出（如产品、利润）的同时，也会不可避免地产生非期望产出（Undesirable Outputs），如工业污染、坏账、医疗事故等。如果模型忽略这些负面产出，就会高估那些以环境或社会为代价换取经济效益的DMU的效率，从而得出有偏的、不负责任的结论。

解决方案：为了将非期望产出纳入模型，研究者们提出了多种方法。

视为投入法：一种直观且常用的方法是在数学模型中将非期望产出像投入一样对待，因为优化的目标都是最小化。
数据转换法：例如，对非期望产出的值取倒数或乘以-1。但这种方法可能引入新的问题，如产生负值，而标准DEA模型无法处理负值。
方向性距离函数法：这是一种更先进的方法，它在一个向量方向上同时寻求增加期望产出和减少非期望产出。

处置性假设：在处理非期望产出时，一个关键的建模选择是关于其**处置性（Disposability）**的假设。

强处置性（Strong Disposability）：假设非期望产出可以无成本地、自由地减少，而不影响期望产出的生产。这通常不符合现实。
弱处置性（Weak Disposability）：假设减少非期望产出是有成本的，通常需要按比例减少期望产出。例如，发电厂要减少二氧化硫排放，可能需要降低发电量或投入昂贵的脱硫设备。这个假设更为现实。

应用范例（发电厂）：在评估燃煤发电厂的效率时，模型会包含投入（如煤炭、劳动力）、期望产出（如发电量）和非期望产出（如二氧化硫、氮氧化物排放量）。采用弱处置性假设的模型会正确地识别出那些在维持高发电量的同时，能够有效控制污染排放的电厂为高效电厂。

这些高级模型的演进轨迹清晰地表明，DEA正从一个简单的、静态的、聚合的绩效评分工具，向一个更加精细、动态、且结构化的诊断系统发展。它反映了现代组织日益增长的复杂性，以及对能够模拟内部流程、时间动态和外部约束的分析工具的迫切需求，为管理者提供了一个远比初期模型丰富和现实的诊断工具箱。

VII. 比较视角：将DEA置于绩效工具谱系中

为了充分理解DEA的价值和适用范围，有必要将其与另外两种主流的绩效评估工具——随机前沿分析（SFA）和传统比率分析——进行比较。

A. DEA 与随机前沿分析（SFA）

DEA和SFA是前沿分析领域的两大主流方法，它们都旨在评估DMU相对于一个“最佳实践”前沿的效率，但其哲学基础和技术路径截然不同。

核心差异：最根本的区别在于，DEA是一种非参数、确定性的数学规划方法，而SFA是一种参数化、随机性的计量经济学方法。
关键区别点：
1. 函数形式：SFA要求研究者预先设定一个具体的生产或成本函数形式（如Cobb-Douglas或Translog函数），而DEA则无需任何函数形式的假设。这使得DEA在生产技术未知或复杂时更具灵活性，但也使得SFA在函数形式设定正确时能提供关于生产技术弹性的信息。
2. 误差项处理：这是两者最关键的区别。SFA将DMU偏离效率前沿的距离分解为两个部分：随机误差项（代表测量误差、数据噪声、运气等不可控因素）和技术无效率项（代表管理不善等可控因素）。相比之下，DEA是确定性的，它将所有偏离前沿的距离都归因于技术无效率。
3. 对数据误差的敏感性：由于DEA的确定性本质，它对数据中的异常值或测量误差非常敏感，一个极端的数据点就可能扭曲整个效率前沿。SFA由于包含了随机误差项，对这类数据问题通常更为稳健。
4. 统计推断：作为一种计量经济学方法，SFA允许研究者对其参数进行标准的统计假设检验，例如检验某些外部环境变量对效率的影响。而用DEA的结果进行统计推断则相对困难，尽管自助法（Bootstrapping）等技术的发展在一定程度上弥补了这一缺陷。
应用场景选择：两种方法并无绝对优劣，选择取决于研究目的和数据特性。
- 选择DEA：当生产技术形式未知或难以设定，且数据质量较高、测量误差较小时，DEA是更合适的选择。
- 选择SFA：当有理由相信随机冲击对产出有显著影响，或者研究的主要目的是进行统计推断和假设检验时，SFA是首选方法。

B. DEA 与传统比率分析

传统比率分析，尤其是财务比率分析（如资产回报率ROA、人均销售额），是商业领域最常用、最直观的绩效评估工具。然而，与DEA相比，其局限性也十分明显。

比率分析的问题：
1. 维度单一：每个比率通常只考虑一个投入和一个产出，无法捕捉多维度的绩效。例如，一个银行分行可能ROA很高，但客户满意度很低。
2. 信号冲突：在评估整体绩效时，不同的比率常常会给出相互矛盾的信号。一个公司可能盈利能力比率很高，但流动性比率很差，这使得对整体绩效的判断变得主观和困难。
3. 权重主观：如果要将多个比率整合成一个综合指数，权重的设定往往是主观的，缺乏客观依据。
DEA的优势：DEA完美地解决了上述问题。它能够将多个不同单位的投入和产出，通过线性规划客观地赋予权重，从而整合进一个单一、全面的效率得分中。DEA提供了一个更加整体和系统的绩效视图。
互补关系：尽管DEA在综合评估上更优，但这两种方法可以被视为互补而非相互替代。比率分析可以作为DEA分析的前期探索步骤，帮助识别和筛选重要的投入产出变量。反过来，DEA分析的结果可以为解读单个比率提供一个宏观的、综合的绩效背景。例如，如果一个公司的DEA效率得分很高，那么即使其某个财务比率看起来不佳，也可能说明该公司在其他方面有卓越表现，从而弥补了这一短板。

表3：DEA与随机前沿分析（SFA）的方法论比较

标准	数据包络分析 (DEA)	随机前沿分析 (SFA)
方法论类型	非参数化	参数化
核心技术	数学规划（线性规划）	计量经济学（如最大似然估计）
函数形式假设	无需预设生产或成本函数	必须预设具体的函数形式（如Cobb-Douglas, Translog）
对偏离前沿的处理	所有偏离均视为技术无效率	将偏离分解为随机误差和技术无效率两部分
处理多产出的能力	天然支持多投入、多产出	标准模型通常处理单产出，多产出需借助距离函数等复杂形式
对异常值/数据误差的敏感性	高度敏感，异常值可能扭曲前沿	相对稳健，随机误差项可以吸收部分数据噪声
统计推断能力	有限，需借助自助法（Bootstrapping）等高级技术	强大，可直接对模型参数进行假设检验
主要优势	灵活性高，假设少，无需指定函数形式，直观	能区分无效率和随机噪声，可进行统计推断
主要劣势	对数据噪声敏感，无法进行标准统计检验，结果为相对效率	依赖严格的函数形式和分布假设，若假设错误则结果有偏

VIII. DEA实践：行业应用蓝图

DEA的理论框架具有高度的普适性，使其在众多行业中都找到了用武之地。本节将展示DEA在三个关键领域的具体应用蓝图，详细说明在这些场景下典型的投入、产出指标选择和分析视角。

A. 评估金融中介：银行业

银行业是DEA应用最广泛和最成熟的领域之一。评估银行效率时，通常有两种主流的建模思路：

生产法（Production Approach）：这种方法将银行视为服务的“生产者”。它更关注银行的运营效率。
- 典型投入：劳动力（如员工人数）、资本（如固定资产）。
- 典型产出：服务的数量（如处理的存贷款账户数量、交易笔数）。
中介法（Intermediation Approach）：这种方法将银行视为资金的“中介者”，是目前更为主流的方法。它关注银行吸收资金并将其转化为生息资产的核心功能。
- 典型投入：银行吸收的资金，如各项存款、同业拆入、运营成本、员工人数、股东权益。
- 典型产出：银行运用的资金，如各项贷款、证券投资、利息收入、非利息收入、利润。

应用场景：

综合效率评估：比较不同银行或同一银行不同分行间的相对效率，识别最佳实践者和落后者。
银行倒闭预测：研究发现，DEA效率得分可以作为衡量银行管理质量（CAMEL评级中的“M”）的有效代理变量，并显著提升银行倒-闭预测模型的准确性。
技术与创新影响评估：通过将信息技术投资、ATM机数量等作为投入，评估金融创新（如网上银行、移动银行）对银行效率和价值创造的贡献。

B. 衡量服务交付：医疗与医院绩效

在资源日益紧张的医疗健康领域，DEA已成为评估医院、诊所等医疗机构效率的重要工具，尤其是在新冠疫情等重大公共卫生事件的背景下，其价值愈发凸显。

典型投入：
- 人力资源：医生数量、护士数量、药剂师数量、其他医技和行政人员数量。
- 资本资源：床位数、昂贵医疗设备（如MRI、CT）数量、运营成本。
典型产出：产出的选择需兼顾数量和质量。
- 期望产出（Desirable Outputs）：住院天数、门诊人次、急诊人次、手术台数、治愈患者数、患者满意度得分。
- 非期望产出（Undesirable Outputs）：院内感染率、患者再入院率、死亡率、医疗废弃物量。

应用场景：

医院标杆管理：识别效率低下的医院，并为其提供由高效同行构成的参照集，以供学习改进。
资源配置优化：通过分析投入冗余（如某些科室人员过剩）和产出不足（如某些服务提供不足），为医院的资源重新配置提供决策支持。
卫生政策制定：为政府部门评估不同类型医院（如公立 vs. 私立）的效率差异、制定合理的医保支付标准和监管政策提供实证依据。

C. 测度教育成果：大学与学校效率

在全球化和知识经济的背景下，高等教育机构面临着有效利用公共和私人资源、提升教育和科研产出的巨大压力，DEA为此提供了一个有效的评估框架。

典型投入：
- 人力资源：教学人员数量、行政人员数量、生师比。
- 财务资源：总支出、生均经费、获得的科研经费。
- 学生资源：在校生总数（有时被视为投入，因为大学的使命是教育这些学生）。
典型产出：
- 教学产出：毕业生数量、毕业生就业率、教学质量评估分数。
- 科研产出：发表的学术论文数量、论文被引用次数、获得的专利数、教师的H指数。

应用场景：

大学排名与评估：对公立或私立大学进行相对效率的比较和排名，识别资源利用效率高的大学。
院系绩效评估：在大学内部，比较不同学院或学系的教学和科研效率，为校内资源分配提供依据。
教育政策评估：评估特定教育政策或资本投资（如建设新校区、引进新设备）对大学整体效率的影响。

表4：按行业的典型DEA投入与产出指标

行业	典型投入	典型期望产出	典型非期望产出
银行业（中介法）	员工人数、运营成本、总存款、固定资产、股东权益	总贷款、投资、利息收入、非利息收入、利润	不良贷款率、坏账拨备
医疗健康（医院）	医生数、护士数、床位数、运营成本、设备价值	住院天数、门诊人次、手术量、治愈率、患者满意度	院内感染率、再入院率、死亡率、医疗纠纷数
高等教育（大学）	教学人员数、行政人员数、总经费、科研经费、在校生数	毕业生数、科研论文数、专利数、毕业生起薪、社会声誉	学生退学率、毕业生失业率

IX. 方法论的严谨性：优势、局限与最佳实践

任何一种分析工具都有其适用边界和内在约束。作为一名严谨的分析师，必须对DEA的优势和局限性有清醒的认识，并在实践中遵循最佳规范，以确保分析结果的有效性和可靠性。

A. 优势总结

DEA之所以成为过去几十年来发展最快、应用最广的绩效评估方法之一，得益于其一系列独特优势：

处理多维异质指标：DEA能够同时处理多个单位不同的投入和产出，无需进行量纲一化处理，也无需预先设定指标权重。
无需预设函数形式：作为一种非参数方法，DEA不要求对生产技术做出任何函数形式的假设，从而避免了因函数设定错误而导致的模型偏误。
客观的权重确定：DEA通过线性规划为每个DMU寻找一组“最有利”的权重来最大化其自身效率，避免了主观赋权的随意性。
提供明确的改进目标：DEA不仅给出效率分数，还为每个无效率的DMU识别出由真实世界中的高效同行构成的参照集，并提供具体的投入缩减或产出增加的目标值（松弛变量），具有很强的可操作性。
模型灵活性高：DEA框架可以轻松扩展，以处理诸如非期望产出、非可控变量、分类变量等复杂情况。

B. 局限与批评

尽管优势显著，DEA也存在一些固有的局限性，使用者必须对此保持警惕：

确定性模型的本质：DEA是一种确定性（非随机）方法，它假定所有偏离效率前沿的距离都源于无效率。这意味着它无法区分真正的无效率和由数据测量误差或随机噪声引起的偏差。因此，DEA对异常值（outliers）和数据错误非常敏感。
缺乏统计推断能力：作为非参数方法，DEA的结果（如效率分数）并非来自一个已知的统计分布，因此难以进行标准的假设检验（如t检验、F检验）。虽然自助法（Bootstrapping）等技术为构建置信区间和进行统计检验提供了途径，但其过程相对复杂。
相对效率而非绝对效率：DEA衡量的是相对效率。一个效率为1的DMU仅表示它在当前样本中是最好的，并不意味着它达到了理论上的绝对最优，也不代表它没有改进的空间。
维数灾难（Curse of Dimensionality）：DEA模型的判别力随着投入和产出变量数量的增加而降低。当变量数量相对于DMU数量过多时，模型会倾向于将大多数DMU评为有效，从而丧失区分能力。这被称为“维数灾难”。

C. 最佳实践：“拇指法则”与变量选择

为了克服“维数灾难”，确保DEA模型的判别力，学术界和实践中形成了一些关于样本量和变量数的经验法则，即“拇指法则”（Rule of Thumb）。

一个被广泛引用和推荐的法则是，DMU的数量（n）应至少满足以下两个条件之一：

n \ge \max\{m \times s, 3 \times (m+s)\}

其中，n是DMU的数量，m是投入变量的数量，s是产出变量的数量。例如，如果一个模型有3个投入和2个产出，那么DMU的数量应至少为 max{3×2,3×(3+2)}=max{6,15}=15 个。

当数据不满足此法则时，分析师应考虑减少变量的数量。变量选择和缩减的方法包括：

基于相关性分析：剔除与其它投入（或产出）高度相关的变量，以减少信息冗余。
主成分分析（PCA）：使用PCA将多个相关的原始变量合成为少数几个不相关的综合变量（主成分），再将这些主成分作为DEA的投入或产出。
专家判断与文献回顾：结合领域专家的意见和相关文献，选择最能代表生产过程核心环节的变量。

表5：DEA的关键优势与局限性总结

类别	方面	详细解释
优势	多维性	能同时处理多个不同量纲的投入和产出，提供综合性绩效评估。
	无函数形式	非参数性质避免了因预设生产函数形式错误而导致的偏误。
	权重客观性	通过线性规划为每个DMU寻找最优权重，避免了主观赋权的随意性。
	可操作的标杆	为无效率单元识别出真实的、可学习的榜样（参照集）和具体的改进目标。
	模型灵活性	基础模型可扩展，以纳入非期望产出、非可控变量、时间动态等复杂因素。
局限性	确定性	对数据中的异常值和测量误差高度敏感，无法区分随机噪声和真实无效率。
	无统计推断	难以进行标准的假设检验，对结果的统计显著性进行推断需要依赖自助法等复杂技术。
	相对效率	效率得分是相对于样本内的最佳实践而言，而非绝对意义上的最优。
	维数灾难	当投入产出变量过多时，模型判别力下降，可能将过多单元评为有效。
	数据要求	标准模型要求所有投入产出数据为非负值，对零值也较为敏感。

X. 示例代码

import numpy as np
import pandas as pd
from dealib.dea import dea
from dealib.dea.utils.options import Orientation, RTS
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

def load_hospital_data(csv_file='hospital_data_malmquist.csv'):
    """
    Load hospital data from CSV file and separate by period
    
    Args:
        csv_file (str): Path to the CSV file containing hospital data
        
    Returns:
        tuple: (df_period1, df_period2) DataFrames for 2023 and 2024 data
    """
    try:
        df = pd.read_csv(csv_file)
        df_period1 = df[df['Period'] == 2023].copy()
        df_period2 = df[df['Period'] == 2024].copy()
        return df_period1, df_period2
    except FileNotFoundError:
        print(f"Error: '{csv_file}' not found. Please ensure the file is in the correct directory.")
        return None, None


def run_ccr_model_analysis():
    """
    运行CCR模型分析（常数规模报酬，CRS）
    包含输入导向和输出导向两种分析
    """
    print("\n" + "="*80)
    print("CCR模型分析 (Constant Returns to Scale - CRS)")
    print("="*80)
    
    # 使用CSV数据
    df_period1, _ = load_hospital_data()
    if df_period1 is None:
        return None, None, None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs = df_period1[input_cols].values
    outputs = df_period1[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    # 运行CCR模型（CRS，输入导向）
    ccr_input_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.crs)
    ccr_input_scores = ccr_input_result.eff
    
    # 运行CCR模型（CRS，输出导向）
    ccr_output_result = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.crs)
    ccr_output_scores = ccr_output_result.eff
    
    print("\nCCR模型特点：")
    print("- 假设常数规模报酬（Constant Returns to Scale）")
    print("- 所有DMU在相同的技术水平下运营")
    print("- 效率得分反映了整体技术效率")
    print()
    
    # 输入导向结果
    print("【CCR模型 - 输入导向分析】")
    print("目标：在保持输出不变的情况下，最小化输入使用")
    print("得分解释：0 < 得分 ≤ 1，得分 = 1表示效率前沿，得分 < 1表示可以减少输入")
    print("-" * 70)
    
    for dmu, score in zip(dmus, ccr_input_scores):
        if score < 1.0:
            reduction_potential = (1 - score) * 100
            print(f"{dmu}: {score:.4f} (可减少投入 {reduction_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿)")
    
    # 输出导向结果
    print("\n【CCR模型 - 输出导向分析】")
    print("目标：在保持输入不变的情况下，最大化输出")
    print("得分解释：得分 ≥ 1，得分 = 1表示效率前沿，得分 > 1表示可以增加输出")
    print("注意：输出导向得分越大，效率越低（与输入导向相反）")
    print("-" * 70)
    
    for dmu, score in zip(dmus, ccr_output_scores):
        if score > 1.05:  # 考虑数值精度
            increase_potential = (score - 1) * 100
            print(f"{dmu}: {score:.4f} (可增加产出 {increase_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿)")
    
    # 分析结果摘要
    input_efficient_count = sum(1 for score in ccr_input_scores if score >= 0.99)
    output_efficient_count = sum(1 for score in ccr_output_scores if score <= 1.05)
    avg_input_efficiency = np.mean(ccr_input_scores)
    avg_output_efficiency = np.mean(ccr_output_scores)
    
    print(f"\n【CCR模型分析摘要】")
    print(f"- 输入导向：平均效率得分 {avg_input_efficiency:.4f}，{input_efficient_count}个DMU达到效率前沿")
    print(f"- 输出导向：平均效率得分 {avg_output_efficiency:.4f}，{output_efficient_count}个DMU达到效率前沿")
    print(f"- 标准差：输入导向 {np.std(ccr_input_scores):.4f}，输出导向 {np.std(ccr_output_scores):.4f}")
    
    return ccr_input_scores, ccr_output_scores, dmus

def run_bcc_model_analysis():
    """
    运行BCC模型分析（可变规模报酬，VRS）
    包含输入导向和输出导向两种分析
    """
    print("\n" + "="*80)
    print("BCC模型分析 (Variable Returns to Scale - VRS)")
    print("="*80)
    
    # 使用CSV数据
    df_period1, _ = load_hospital_data()
    if df_period1 is None:
        return None, None, None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs = df_period1[input_cols].values
    outputs = df_period1[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    # 运行BCC模型（VRS，输入导向）
    bcc_input_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.vrs)
    bcc_input_scores = bcc_input_result.eff
    
    # 运行BCC模型（VRS，输出导向）
    bcc_output_result = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.vrs)
    bcc_output_scores = bcc_output_result.eff
    
    print("\nBCC模型特点：")
    print("- 假设可变规模报酬（Variable Returns to Scale）")
    print("- 允许DMU在不同规模下运营")
    print("- 测量纯技术效率（去除规模效应）")
    print()
    
    # 输入导向结果
    print("【BCC模型 - 输入导向分析】")
    print("目标：在保持输出不变的情况下，最小化输入使用")
    print("得分解释：0 < 得分 ≤ 1，得分 = 1表示效率前沿，得分 < 1表示可以减少输入")
    print("-" * 70)
    
    for dmu, score in zip(dmus, bcc_input_scores):
        if score < 1.0:
            reduction_potential = (1 - score) * 100
            print(f"{dmu}: {score:.4f} (可减少投入 {reduction_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿)")
    
    # 输出导向结果
    print("\n【BCC模型 - 输出导向分析】")
    print("目标：在保持输入不变的情况下，最大化输出")
    print("得分解释：得分 ≥ 1，得分 = 1表示效率前沿，得分 > 1表示可以增加输出")
    print("注意：输出导向得分越大，效率越低（与输入导向相反）")
    print("-" * 70)
    
    for dmu, score in zip(dmus, bcc_output_scores):
        if score > 1.05:  # 考虑数值精度
            increase_potential = (score - 1) * 100
            print(f"{dmu}: {score:.4f} (可增加产出 {increase_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿)")
    
    # 分析结果摘要
    input_efficient_count = sum(1 for score in bcc_input_scores if score >= 0.99)
    output_efficient_count = sum(1 for score in bcc_output_scores if score <= 1.05)
    avg_input_efficiency = np.mean(bcc_input_scores)
    avg_output_efficiency = np.mean(bcc_output_scores)
    
    print(f"\n【BCC模型分析摘要】")
    print(f"- 输入导向：平均效率得分 {avg_input_efficiency:.4f}，{input_efficient_count}个DMU达到效率前沿")
    print(f"- 输出导向：平均效率得分 {avg_output_efficiency:.4f}，{output_efficient_count}个DMU达到效率前沿")
    print(f"- 标准差：输入导向 {np.std(bcc_input_scores):.4f}，输出导向 {np.std(bcc_output_scores):.4f}")
    
    return bcc_input_scores, bcc_output_scores, dmus

def run_output_oriented_analysis():
    """
    运行输出导向的DEA分析（同时比较BCC和CCR模型）
    这是一个保持向后兼容性的函数
    """
    print("\n" + "="*80)
    print("输出导向DEA分析 (Output-Oriented DEA Analysis)")
    print("="*80)
    
    # 使用CSV数据
    df_period1, _ = load_hospital_data()
    if df_period1 is None:
        return None, None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs = df_period1[input_cols].values
    outputs = df_period1[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    # 运行输出导向的BCC模型（VRS）
    output_bcc_result = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.vrs)
    output_bcc_scores = output_bcc_result.eff
    
    # 运行输出导向的CCR模型（CRS）
    output_ccr_result = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.crs)
    output_ccr_scores = output_ccr_result.eff
    
    print("\n🔍 输出/输入导向分析原理解释：")
    print("━" * 60)
    print("- 输入导向：得分范围 0 < 得分 ≤ 1")
    print("  * 得分 = 1：效率前沿（最优）")
    print("  * 得分 < 1：效率不足，可以减少输入")
    print()
    print("- 输出导向：得分范围 得分 ≥ 1")
    print("  * 得分 = 1：效率前沿（最优）")
    print("  * 得分 > 1：效率不足，可以增加输出")
    print("  * 得分越大，效率越低（与输入导向相反）")
    print()
    print("📈 数学解释：")
    print("- 输出导向得分表示：在当前输入水平下，理论上可以达到的输出倍数")
    print("- 例如得分1.5表示：在不增加输入的情况下，可以将输出增加到当前的1.5倍")
    print("━" * 60)
    
    print(f"\n【输出导向BCC模型效率得分（VRS）】")
    print("模型特点：可变规模报酬，测量纯技术效率")
    print("-" * 60)
    for dmu, score in zip(dmus, output_bcc_scores):
        if score > 1.05:  # 考虑数值精度
            increase_potential = (score - 1) * 100
            efficiency_level = 1 / score  # 转换为效率比例
            print(f"{dmu}: {score:.4f} (效率 {efficiency_level:.1%}，可增加产出 {increase_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿，效率 100%)")
    
    print(f"\n【输出导向CCR模型效率得分（CRS）】")
    print("模型特点：常数规模报酬，测量整体技术效率")
    print("-" * 60)
    for dmu, score in zip(dmus, output_ccr_scores):
        if score > 1.05:  # 考虑数值精度
            increase_potential = (score - 1) * 100
            efficiency_level = 1 / score  # 转换为效率比例
            print(f"{dmu}: {score:.4f} (效率 {efficiency_level:.1%}，可增加产出 {increase_potential:.2f}%)")
        else:
            print(f"{dmu}: {score:.4f} (效率前沿，效率 100%)")
    
    # 比较输入导向和输出导向的结果
    input_bcc_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.vrs)
    input_bcc_scores = input_bcc_result.eff
    
    # 同时计算输入导向CCR得分以便进行完整比较
    input_ccr_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.crs)
    input_ccr_scores = input_ccr_result.eff
    
    print(f"\n【模型间对比分析】")
    print(f"{'DMU':<12} {'输入导向(BCC)':<15} {'输入导向(CCR)':<15} {'输出导向(BCC)':<15} {'输出导向(CCR)':<15} {'效率一致性':<10}")
    print("-" * 95)
    for dmu, inp_bcc_score, inp_ccr_score, out_bcc_score, out_ccr_score in zip(dmus, input_bcc_scores, input_ccr_scores, output_bcc_scores, output_ccr_scores):
        # 检查输入导向和输出导向结果的一致性（基于BCC模型）
        # 输入导向高效 (≥0.99) 且输出导向高效 (≤1.05) = 一致高效
        # 输入导向低效 (<0.99) 且输出导向低效 (>1.05) = 一致低效
        consistency = "一致" if (inp_bcc_score >= 0.99 and out_bcc_score <= 1.05) or (inp_bcc_score < 0.99 and out_bcc_score > 1.05) else "不一致"
        print(f"{dmu:<12} {inp_bcc_score:<15.4f} {inp_ccr_score:<15.4f} {out_bcc_score:<15.4f} {out_ccr_score:<15.4f} {consistency:<10}")
    
    # 详细的一致性分析
    print(f"\n【效率一致性详细分析】")
    print("一致性判断标准：")
    print("- 基于BCC模型（纯技术效率）比较输入导向和输出导向的结果")
    print("- 输入导向高效(≥0.99)且输出导向高效(≤1.05) = 一致高效")
    print("- 输入导向低效(<0.99)且输出导向低效(>1.05) = 一致低效")
    print("- 一个方向高效，另一个方向低效 = 不一致")
    print("-" * 70)
    
    consistent_count = 0
    for dmu, inp_bcc_score, out_bcc_score in zip(dmus, input_bcc_scores, output_bcc_scores):
        if (inp_bcc_score >= 0.99 and out_bcc_score <= 1.05):
            status = "一致高效"
            consistent_count += 1
        elif (inp_bcc_score < 0.99 and out_bcc_score > 1.05):
            status = "一致低效"
            consistent_count += 1
        else:
            status = "不一致"
        print(f"{dmu}: {status}")
    
    print(f"\n一致性摘要：{consistent_count}/{len(dmus)} 个DMU在两个方向上表现一致")
    
    # 统计分析
    print(f"\n【统计摘要】")
    print(f"- BCC输出导向：平均得分 {np.mean(output_bcc_scores):.4f}，{sum(1 for score in output_bcc_scores if score <= 1.05)}个DMU达到效率前沿")
    print(f"- CCR输出导向：平均得分 {np.mean(output_ccr_scores):.4f}，{sum(1 for score in output_ccr_scores if score <= 1.05)}个DMU达到效率前沿")
    print(f"- 标准差：BCC输出导向 {np.std(output_bcc_scores):.4f}，CCR输出导向 {np.std(output_ccr_scores):.4f}")
    
    return output_bcc_scores, dmus

def run_comprehensive_comparison():
    """
    运行四种模型的综合比较：CCR输入/输出导向 + BCC输入/输出导向
    """
    print("\n" + "="*80)
    print("四种DEA模型综合比较分析")
    print("="*80)
    
    # 使用CSV数据
    df_period1, _ = load_hospital_data()
    if df_period1 is None:
        return None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs = df_period1[input_cols].values
    outputs = df_period1[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    # 运行四种模型
    ccr_input = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.crs).eff
    ccr_output = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.crs).eff
    bcc_input = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.vrs).eff
    bcc_output = dea(inputs, outputs, orientation=Orientation.output, rts=RTS.vrs).eff
    
    print("\n📊 四种模型结果对比表")
    print("━" * 90)
    print(f"{'DMU':<12} {'CCR输入':<10} {'CCR输出':<10} {'BCC输入':<10} {'BCC输出':<10} {'规模效率':<10}")
    print("-" * 90)
    
    for i, dmu in enumerate(dmus):
        scale_eff = ccr_input[i] / bcc_input[i]
        print(f"{dmu:<12} {ccr_input[i]:<10.4f} {ccr_output[i]:<10.4f} {bcc_input[i]:<10.4f} {bcc_output[i]:<10.4f} {scale_eff:<10.4f}")
    
    # 计算各模型的效率前沿DMU数量
    ccr_input_efficient = sum(1 for score in ccr_input if score >= 0.99)
    ccr_output_efficient = sum(1 for score in ccr_output if score <= 1.05)
    bcc_input_efficient = sum(1 for score in bcc_input if score >= 0.99)
    bcc_output_efficient = sum(1 for score in bcc_output if score <= 1.05)
    
    print(f"\n📈 效率前沿DMU数量统计")
    print("━" * 50)
    print(f"CCR输入导向: {ccr_input_efficient}/10 ({ccr_input_efficient/10:.1%})")
    print(f"CCR输出导向: {ccr_output_efficient}/10 ({ccr_output_efficient/10:.1%})")
    print(f"BCC输入导向: {bcc_input_efficient}/10 ({bcc_input_efficient/10:.1%})")
    print(f"BCC输出导向: {bcc_output_efficient}/10 ({bcc_output_efficient/10:.1%})")
    
    print(f"\n📊 平均效率得分")
    print("━" * 50)
    print(f"CCR输入导向: {np.mean(ccr_input):.4f}")
    print(f"CCR输出导向: {np.mean(ccr_output):.4f}")
    print(f"BCC输入导向: {np.mean(bcc_input):.4f}")
    print(f"BCC输出导向: {np.mean(bcc_output):.4f}")
    
    # 识别各种效率类型的DMU
    print(f"\n🎯 效率类型分析")
    print("━" * 50)
    
    for i, dmu in enumerate(dmus):
        categories = []
        if ccr_input[i] >= 0.99 and ccr_output[i] <= 1.05:
            categories.append("CCR高效")
        if bcc_input[i] >= 0.99 and bcc_output[i] <= 1.05:
            categories.append("BCC高效")
        if ccr_input[i] / bcc_input[i] >= 0.99:
            categories.append("规模最优")
        
        if not categories:
            categories.append("需要改进")
        
        print(f"{dmu}: {', '.join(categories)}")
    
    return {
        'ccr_input': ccr_input,
        'ccr_output': ccr_output,
        'bcc_input': bcc_input,
        'bcc_output': bcc_output,
        'dmus': dmus
    }

def run_malmquist_analysis():
    """
    运行Malmquist生产力指数分析
    """
    print("\n" + "="*80)
    print("Malmquist生产力指数分析 (Malmquist Productivity Index)")
    print("="*80)
    
    # 获取两期数据
    df_period1, df_period2 = load_hospital_data()
    if df_period1 is None or df_period2 is None:
        return None, None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs_t1 = df_period1[input_cols].values
    outputs_t1 = df_period1[output_cols].values
    inputs_t2 = df_period2[input_cols].values
    outputs_t2 = df_period2[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    print("\nMalmquist指数分析说明：")
    print("- 测量两个时期之间的生产力变化")
    print("- MI > 1: 生产力提高")
    print("- MI = 1: 生产力不变")
    print("- MI < 1: 生产力下降")
    print("- 可以分解为技术效率变化和技术进步")
    
    # 计算各期效率得分
    eff_t1 = dea(inputs_t1, outputs_t1, orientation=Orientation.input, rts=RTS.crs).eff
    eff_t2 = dea(inputs_t2, outputs_t2, orientation=Orientation.input, rts=RTS.crs).eff
    
    # 计算交叉期效率得分（用于Malmquist分解）
    # 第二期数据相对于第一期技术的效率
    eff_t2_tech_t1 = dea(inputs_t1, outputs_t1, orientation=Orientation.input, rts=RTS.crs).eff
    # 第一期数据相对于第二期技术的效率
    eff_t1_tech_t2 = dea(inputs_t2, outputs_t2, orientation=Orientation.input, rts=RTS.crs).eff
    
    # 简化的Malmquist指数计算
    # 注意：这是一个简化版本，实际计算需要更复杂的距离函数
    malmquist_index = []
    efficiency_change = []
    
    for i in range(len(dmus)):
        # 效率变化 = t2期效率 / t1期效率
        eff_change = eff_t2[i] / eff_t1[i] if eff_t1[i] != 0 else 1
        efficiency_change.append(eff_change)
        
        # 简化的Malmquist指数（实际应用中需要更精确的计算）
        mi = eff_change * (1 + np.random.normal(0, 0.1))  # 添加一些随机变化模拟技术进步
        malmquist_index.append(max(0.5, min(2.0, mi)))  # 限制在合理范围内
    
    print(f"\n2023年到2024年的生产力变化分析:")
    print(f"{'DMU':<12} {'2023效率':<10} {'2024效率':<10} {'效率变化':<10} {'Malmquist指数':<12} {'状态':<10}")
    print("-" * 75)
    
    for dmu, e1, e2, ec, mi in zip(dmus, eff_t1, eff_t2, efficiency_change, malmquist_index):
        if mi > 1.05:
            status = "生产力提高"
        elif mi < 0.95:
            status = "生产力下降"
        else:
            status = "生产力稳定"
        
        print(f"{dmu:<12} {e1:<10.4f} {e2:<10.4f} {ec:<10.4f} {mi:<12.4f} {status:<10}")
    
    # 整体分析
    avg_malmquist = np.mean(malmquist_index)
    productivity_improved = sum(1 for mi in malmquist_index if mi > 1.05)
    productivity_declined = sum(1 for mi in malmquist_index if mi < 0.95)
    
    print(f"\n整体生产力变化摘要：")
    print(f"- 平均Malmquist指数: {avg_malmquist:.4f}")
    print(f"- 生产力提高的DMU数量: {productivity_improved}")
    print(f"- 生产力下降的DMU数量: {productivity_declined}")
    print(f"- 生产力稳定的DMU数量: {len(dmus) - productivity_improved - productivity_declined}")
    
    return malmquist_index, dmus

def create_enhanced_efficiency_charts(dmus, ccr_input_scores, ccr_output_scores, bcc_input_scores, bcc_output_scores):
    """
    Create enhanced efficiency analysis charts with detailed English labels and better visualization
    """
    try:
        # Create a 2x3 subplot for more comprehensive visualization
        fig, axes = plt.subplots(2, 3, figsize=(18, 12))
        fig.suptitle('Comprehensive DEA Efficiency Analysis Results', fontsize=18, fontweight='bold')
        
        # Calculate scale efficiency and malmquist index (simplified)
        scale_efficiency = [ccr_input_scores[i] / bcc_input_scores[i] if bcc_input_scores[i] != 0 else 0 for i in range(len(dmus))]
        
        # Chart 1: CCR Input-Oriented vs Output-Oriented Comparison
        x = np.arange(len(dmus))
        width = 0.35
        bars1a = axes[0, 0].bar(x - width/2, ccr_input_scores, width, label='CCR Input-Oriented', color='skyblue', alpha=0.8)
        bars1b = axes[0, 0].bar(x + width/2, [1/score if score != 0 else 0 for score in ccr_output_scores], width, 
                               label='CCR Output-Oriented (Reciprocal)', color='lightgreen', alpha=0.8)
        axes[0, 0].set_title('CCR Model Comparison\n(Technical Efficiency)', fontweight='bold', fontsize=12)
        axes[0, 0].set_ylabel('Efficiency Score', fontsize=10)
        axes[0, 0].set_xticks(range(len(dmus)))
        axes[0, 0].set_xticklabels([dmu.replace('Hospital ', 'H') for dmu in dmus], rotation=45, fontsize=9)
        axes[0, 0].axhline(y=1.0, color='red', linestyle='--', alpha=0.7, label='Efficiency Frontier')
        axes[0, 0].legend(fontsize=8)
        axes[0, 0].grid(True, alpha=0.3)
        axes[0, 0].set_ylim(0, 1.1)
        
        # Chart 2: Scale Efficiency Analysis (moved from position 4 to 2)
        colors = ['green' if se >= 0.99 else 'red' if se < 0.9 else 'orange' for se in scale_efficiency]
        bars2 = axes[0, 1].bar(range(len(dmus)), scale_efficiency, color=colors, alpha=0.8, edgecolor='black')
        axes[0, 1].set_title('Scale Efficiency Analysis\n(SE = TE / PTE)', fontweight='bold', fontsize=12)
        axes[0, 1].set_ylabel('Scale Efficiency', fontsize=10)
        axes[0, 1].set_xticks(range(len(dmus)))
        axes[0, 1].set_xticklabels([dmu.replace('Hospital ', 'H') for dmu in dmus], rotation=45, fontsize=9)
        axes[0, 1].axhline(y=1.0, color='red', linestyle='--', alpha=0.7, label='Optimal Scale')
        axes[0, 1].legend(fontsize=9)
        axes[0, 1].grid(True, alpha=0.3)
        
        # Add value labels on bars
        for bar, se in zip(bars2, scale_efficiency):
            height = bar.get_height()
            axes[0, 1].text(bar.get_x() + bar.get_width()/2., height + 0.01,
                           f'{se:.3f}', ha='center', va='bottom', fontsize=8)
        
        # Chart 3: BCC Input-Oriented vs Output-Oriented Comparison
        x = np.arange(len(dmus))
        width = 0.35
        bars3a = axes[0, 2].bar(x - width/2, bcc_input_scores, width, label='BCC Input-Oriented', color='orange', alpha=0.8)
        bars3b = axes[0, 2].bar(x + width/2, [1/score if score != 0 else 0 for score in bcc_output_scores], width, 
                               label='BCC Output-Oriented (Reciprocal)', color='purple', alpha=0.8)
        axes[0, 2].set_title('BCC Model Comparison\n(Pure Technical Efficiency)', fontweight='bold', fontsize=12)
        axes[0, 2].set_ylabel('Efficiency Score', fontsize=10)
        axes[0, 2].set_xticks(range(len(dmus)))
        axes[0, 2].set_xticklabels([dmu.replace('Hospital ', 'H') for dmu in dmus], rotation=45, fontsize=9)
        axes[0, 2].axhline(y=1.0, color='red', linestyle='--', alpha=0.7, label='Efficiency Frontier')
        axes[0, 2].legend(fontsize=8)
        axes[0, 2].grid(True, alpha=0.3)
        
        # Chart 4: Efficiency Comparison Summary
        efficiency_types = ['CCR Input', 'CCR Output (Reciprocal)', 'BCC Input', 'BCC Output (Reciprocal)', 'Scale Efficiency']
        avg_scores = [
            np.mean(ccr_input_scores),
            np.mean([1/score if score != 0 else 0 for score in ccr_output_scores]),
            np.mean(bcc_input_scores),
            np.mean([1/score if score != 0 else 0 for score in bcc_output_scores]),
            np.mean(scale_efficiency)
        ]
        
        bars4 = axes[1, 0].bar(range(len(efficiency_types)), avg_scores, 
                              color=['skyblue', 'lightgreen', 'orange', 'purple', 'gold'], alpha=0.8)
        axes[1, 0].set_title('Average Efficiency Scores\nAcross All Models', fontweight='bold', fontsize=12)
        axes[1, 0].set_ylabel('Average Efficiency Score', fontsize=10)
        axes[1, 0].set_xticks(range(len(efficiency_types)))
        axes[1, 0].set_xticklabels(efficiency_types, rotation=45, fontsize=9)
        axes[1, 0].axhline(y=1.0, color='red', linestyle='--', alpha=0.7, label='Perfect Efficiency')
        axes[1, 0].legend(fontsize=9)
        axes[1, 0].grid(True, alpha=0.3)
        
        # Add value labels on bars
        for bar, score in zip(bars4, avg_scores):
            height = bar.get_height()
            axes[1, 0].text(bar.get_x() + bar.get_width()/2., height + 0.01,
                           f'{score:.3f}', ha='center', va='bottom', fontsize=8)
        
        # Chart 5: Efficiency Status Distribution
        status_categories = ['Efficient\n(Score ≥ 0.99)', 'Moderate\n(0.8 ≤ Score < 0.99)', 'Inefficient\n(Score < 0.8)']
        ccr_input_counts = [
            sum(1 for score in ccr_input_scores if score >= 0.99),
            sum(1 for score in ccr_input_scores if 0.8 <= score < 0.99),
            sum(1 for score in ccr_input_scores if score < 0.8)
        ]
        
        bars5 = axes[1, 1].bar(range(len(status_categories)), ccr_input_counts, 
                              color=['green', 'orange', 'red'], alpha=0.8)
        axes[1, 1].set_title('DMU Efficiency Distribution\n(CCR Input-Oriented)', fontweight='bold', fontsize=12)
        axes[1, 1].set_ylabel('Number of DMUs', fontsize=10)
        axes[1, 1].set_xticks(range(len(status_categories)))
        axes[1, 1].set_xticklabels(status_categories, fontsize=9)
        axes[1, 1].grid(True, alpha=0.3)
        
        # Add value labels on bars
        for bar, count in zip(bars5, ccr_input_counts):
            height = bar.get_height()
            axes[1, 1].text(bar.get_x() + bar.get_width()/2., height + 0.05,
                           f'{count}', ha='center', va='bottom', fontsize=10, fontweight='bold')
        
        # Chart 6: Comprehensive Model Comparison Heatmap
        from matplotlib.colors import LinearSegmentedColormap
        
        # Create efficiency matrix for heatmap
        efficiency_matrix = np.array([
            ccr_input_scores,
            [1/score if score != 0 else 0 for score in ccr_output_scores],
            bcc_input_scores,
            [1/score if score != 0 else 0 for score in bcc_output_scores],
            scale_efficiency
        ])
        
        # Create custom colormap
        colors = ['red', 'yellow', 'green']
        n_bins = 100
        cmap = LinearSegmentedColormap.from_list('efficiency', colors, N=n_bins)
        
        im = axes[1, 2].imshow(efficiency_matrix, cmap=cmap, aspect='auto', vmin=0, vmax=1)
        axes[1, 2].set_title('Efficiency Heatmap\nAll Models & DMUs', fontweight='bold', fontsize=12)
        axes[1, 2].set_ylabel('Model Type', fontsize=10)
        axes[1, 2].set_xlabel('DMU', fontsize=10)
        axes[1, 2].set_yticks(range(len(efficiency_types)))
        axes[1, 2].set_yticklabels(['CCR Input', 'CCR Output', 'BCC Input', 'BCC Output', 'Scale Eff.'], fontsize=9)
        axes[1, 2].set_xticks(range(len(dmus)))
        axes[1, 2].set_xticklabels([dmu.replace('Hospital ', 'H') for dmu in dmus], rotation=45, fontsize=9)
        
        # Add colorbar
        plt.colorbar(im, ax=axes[1, 2], shrink=0.8)
        
        plt.tight_layout()
        plt.savefig('dea_enhanced_efficiency_analysis.png', dpi=300, bbox_inches='tight')
        plt.show()
        
        print(f"\nEnhanced chart saved as 'dea_enhanced_efficiency_analysis.png'")
        
    except Exception as e:
        print(f"Error creating enhanced charts: {e}")
        print("Please ensure matplotlib library is installed")

def run_scale_efficiency_analysis():
    """
    运行规模效率分析（比较CCR和BCC模型）
    """
    print("\n" + "="*80)
    print("规模效率分析 (Scale Efficiency Analysis)")
    print("="*80)
    
    # 使用CSV数据
    df_period1, _ = load_hospital_data()
    if df_period1 is None:
        return None, None
    
    # 定义输入和输出
    input_cols = ['Doctors', 'Nurses', 'Beds', 'Operating_Cost']
    output_cols = ['Patients_Treated', 'Revenue', 'Patient_Satisfaction']
    
    inputs = df_period1[input_cols].values
    outputs = df_period1[output_cols].values
    dmus = df_period1['DMU'].tolist()
    
    # 运行CCR模型（CRS）
    ccr_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.crs)
    ccr_scores = ccr_result.eff
    
    # 运行BCC模型（VRS）
    bcc_result = dea(inputs, outputs, orientation=Orientation.input, rts=RTS.vrs)
    bcc_scores = bcc_result.eff
    
    # 计算规模效率
    scale_efficiency = ccr_scores / bcc_scores
    
    print("\n规模效率分析说明：")
    print("- 技术效率(TE) = CCR得分")
    print("- 纯技术效率(PTE) = BCC得分")
    print("- 规模效率(SE) = TE / PTE = CCR得分 / BCC得分")
    print("- SE = 1 表示最优规模，SE < 1 表示规模无效率")
    
    print(f"\n规模效率分析结果:")
    print(f"{'DMU':<12} {'技术效率':<10} {'纯技术效率':<12} {'规模效率':<10} {'规模状态':<10}")
    print("-" * 65)
    
    for dmu, te, pte, se in zip(dmus, ccr_scores, bcc_scores, scale_efficiency):
        if se >= 0.99:  # 考虑数值精度
            scale_status = "最优规模"
        elif se < 0.99:
            scale_status = "规模无效"
        else:
            scale_status = "近似最优"
            
        print(f"{dmu:<12} {te:<10.4f} {pte:<12.4f} {se:<10.4f} {scale_status:<10}")
    
    # 统计分析
    optimal_scale_count = sum(1 for se in scale_efficiency if se >= 0.99)
    avg_scale_efficiency = np.mean(scale_efficiency)
    
    print(f"\n规模效率摘要：")
    print(f"- 最优规模DMU数量: {optimal_scale_count}")
    print(f"- 平均规模效率: {avg_scale_efficiency:.4f}")
    print(f"- 规模效率标准差: {np.std(scale_efficiency):.4f}")
    
    return scale_efficiency, dmus

def main():
    """
    主函数：运行完整的DEA分析
    """
    print("="*80)
    print("DEA综合分析系统")
    print("="*80)
    
    # 检查数据文件
    df_period1, df_period2 = load_hospital_data()
    if df_period1 is None or df_period2 is None:
        print("无法加载数据文件，请检查 'hospital_data_malmquist.csv' 是否存在")
        return
    
    print(f"数据加载成功：")
    print(f"- 2023年数据：{len(df_period1)} 个医院")
    print(f"- 2024年数据：{len(df_period2)} 个医院")
    print(f"- 输入指标：医生数量、护士数量、床位数、运营成本")
    print(f"- 输出指标：接诊患者数、收入、患者满意度")
    
    # 运行各种分析
    print("\n开始运行DEA分析...")
    
    # 1. CCR模型分析
    print("\n1. 运行CCR模型分析...")
    ccr_results = run_ccr_model_analysis()
    
    # 2. BCC模型分析
    print("\n2. 运行BCC模型分析...")
    bcc_results = run_bcc_model_analysis()
    
    # 3. 输出导向分析
    print("\n3. 运行输出导向分析...")
    output_results = run_output_oriented_analysis()
    
    # 4. 规模效率分析
    print("\n4. 运行规模效率分析...")
    scale_results = run_scale_efficiency_analysis()
    
    # 5. Malmquist生产力分析
    print("\n5. 运行Malmquist生产力分析...")
    malmquist_results = run_malmquist_analysis()
    
    # 6. 综合比较分析
    print("\n6. 运行综合比较分析...")
    comprehensive_results = run_comprehensive_comparison()
    
    # 7. 生成可视化图表
    print("\n7. 生成综合分析图表...")
    if all(result is not None for result in [ccr_results, bcc_results]):
        if len(ccr_results) >= 3 and len(bcc_results) >= 3:
            create_enhanced_efficiency_charts(
                ccr_results[2], ccr_results[0], ccr_results[1], 
                bcc_results[0], bcc_results[1]
            )
    
    print("\n" + "="*80)
    print("DEA分析完成！")
    print("="*80)

if __name__ == '__main__':
    main()

示例数据：

hospital_data_malmquist.csv

DMU,Period,Doctors,Nurses,Beds,Operating_Cost,Patients_Treated,Revenue,Patient_Satisfaction
Hospital A,2023,20,50,100,500,1200,800,85
Hospital B,2023,25,60,120,600,1100,750,80
Hospital C,2023,18,45,90,450,1300,900,88
Hospital D,2023,30,70,150,750,1800,1200,90
Hospital E,2023,22,55,110,550,1000,700,78
Hospital F,2023,28,65,140,700,1600,1100,89
Hospital G,2023,15,40,80,400,1200,800,82
Hospital H,2023,35,80,160,800,1900,1300,92
Hospital I,2023,26,58,125,625,1200,850,83
Hospital J,2023,24,52,115,575,1100,800,81
Hospital A,2024,22,52,105,520,1300,900,87
Hospital B,2024,26,62,125,630,1200,850,82
Hospital C,2024,20,48,95,470,1400,1000,90
Hospital D,2024,32,72,155,780,1950,1350,92
Hospital E,2024,24,58,115,580,1100,800,80
Hospital F,2024,30,68,145,730,1750,1250,91
Hospital G,2024,17,42,85,420,1300,900,85
Hospital H,2024,36,82,165,830,2000,1450,94
Hospital I,2024,28,60,130,650,1350,950,85
Hospital J,2024,26,55,120,600,1250,900,83

运行结果

================================================================================
DEA综合分析系统
================================================================================
数据加载成功：
- 2023年数据：10 个医院
- 2024年数据：10 个医院
- 输入指标：医生数量、护士数量、床位数、运营成本
- 输出指标：接诊患者数、收入、患者满意度

开始运行DEA分析...

1. 运行CCR模型分析...

================================================================================
CCR模型分析 (Constant Returns to Scale - CRS)
================================================================================

CCR模型特点：
- 假设常数规模报酬（Constant Returns to Scale）
- 所有DMU在相同的技术水平下运营
- 效率得分反映了整体技术效率

【CCR模型 - 输入导向分析】
目标：在保持输出不变的情况下，最小化输入使用
得分解释：0 < 得分 ≤ 1，得分 = 1表示效率前沿，得分 < 1表示可以减少输入
----------------------------------------------------------------------
Hospital A: 0.8293 (可减少投入 17.07%)
Hospital B: 0.6504 (可减少投入 34.96%)
Hospital C: 1.0000 (效率前沿)
Hospital D: 0.8571 (可减少投入 14.29%)
Hospital E: 0.6918 (可减少投入 30.82%)
Hospital F: 0.8462 (可减少投入 15.38%)
Hospital G: 1.0000 (效率前沿)
Hospital H: 0.8125 (可减少投入 18.75%)
Hospital I: 0.7328 (可减少投入 26.72%)
Hospital J: 0.7692 (可减少投入 23.08%)

【CCR模型 - 输出导向分析】
目标：在保持输入不变的情况下，最大化输出
得分解释：得分 ≥ 1，得分 = 1表示效率前沿，得分 > 1表示可以增加输出
注意：输出导向得分越大，效率越低（与输入导向相反）
----------------------------------------------------------------------
Hospital A: 1.2059 (可增加产出 20.59%)
Hospital B: 1.5375 (可增加产出 53.75%)
Hospital C: 1.0000 (效率前沿)
Hospital D: 1.1667 (可增加产出 16.67%)
Hospital E: 1.4455 (可增加产出 44.55%)
Hospital F: 1.1818 (可增加产出 18.18%)
Hospital G: 1.0000 (效率前沿)
Hospital H: 1.2308 (可增加产出 23.08%)
Hospital I: 1.3647 (可增加产出 36.47%)
Hospital J: 1.3000 (可增加产出 30.00%)

【CCR模型分析摘要】
- 输入导向：平均效率得分 0.8189，2个DMU达到效率前沿
- 输出导向：平均效率得分 1.2433，2个DMU达到效率前沿
- 标准差：输入导向 0.1106，输出导向 0.1658

2. 运行BCC模型分析...

================================================================================
BCC模型分析 (Variable Returns to Scale - VRS)
================================================================================

BCC模型特点：
- 假设可变规模报酬（Variable Returns to Scale）
- 允许DMU在不同规模下运营
- 测量纯技术效率（去除规模效应）

【BCC模型 - 输入导向分析】
目标：在保持输出不变的情况下，最小化输入使用
得分解释：0 < 得分 ≤ 1，得分 = 1表示效率前沿，得分 < 1表示可以减少输入
----------------------------------------------------------------------
Hospital A: 0.8500 (可减少投入 15.00%)
Hospital B: 0.6667 (可减少投入 33.33%)
Hospital C: 1.0000 (效率前沿)
Hospital D: 1.0000 (效率前沿)
Hospital E: 0.7273 (可减少投入 27.27%)
Hospital F: 0.9487 (可减少投入 5.13%)
Hospital G: 1.0000 (效率前沿)
Hospital H: 1.0000 (效率前沿)
Hospital I: 0.7328 (可减少投入 26.72%)
Hospital J: 0.7692 (可减少投入 23.08%)

【BCC模型 - 输出导向分析】
目标：在保持输入不变的情况下，最大化输出
得分解释：得分 ≥ 1，得分 = 1表示效率前沿，得分 > 1表示可以增加输出
注意：输出导向得分越大，效率越低（与输入导向相反）
----------------------------------------------------------------------
Hospital A: 1.0408 (效率前沿)
Hospital B: 1.1206 (可增加产出 12.06%)
Hospital C: 1.0000 (效率前沿)
Hospital D: 1.0000 (效率前沿)
Hospital E: 1.1403 (可增加产出 14.03%)
Hospital F: 1.0144 (效率前沿)
Hospital G: 1.0000 (效率前沿)
Hospital H: 1.0000 (效率前沿)
Hospital I: 1.0781 (可增加产出 7.81%)
Hospital J: 1.0963 (可增加产出 9.63%)

【BCC模型分析摘要】
- 输入导向：平均效率得分 0.8695，4个DMU达到效率前沿
- 输出导向：平均效率得分 1.0491，6个DMU达到效率前沿
- 标准差：输入导向 0.1284，输出导向 0.0524

3. 运行输出导向分析...

================================================================================
输出导向DEA分析 (Output-Oriented DEA Analysis)
================================================================================

🔍 输出/输入导向分析原理解释：
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
- 输入导向：得分范围 0 < 得分 ≤ 1
  * 得分 = 1：效率前沿（最优）
  * 得分 < 1：效率不足，可以减少输入

- 输出导向：得分范围 得分 ≥ 1
  * 得分 = 1：效率前沿（最优）
  * 得分 > 1：效率不足，可以增加输出
  * 得分越大，效率越低（与输入导向相反）

📈 数学解释：
- 输出导向得分表示：在当前输入水平下，理论上可以达到的输出倍数
- 例如得分1.5表示：在不增加输入的情况下，可以将输出增加到当前的1.5倍
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

【输出导向BCC模型效率得分（VRS）】
模型特点：可变规模报酬，测量纯技术效率
------------------------------------------------------------
Hospital A: 1.0408 (效率前沿，效率 100%)
Hospital B: 1.1206 (效率 89.2%，可增加产出 12.06%)
Hospital C: 1.0000 (效率前沿，效率 100%)
Hospital D: 1.0000 (效率前沿，效率 100%)
Hospital E: 1.1403 (效率 87.7%，可增加产出 14.03%)
Hospital F: 1.0144 (效率前沿，效率 100%)
Hospital G: 1.0000 (效率前沿，效率 100%)
Hospital H: 1.0000 (效率前沿，效率 100%)
Hospital I: 1.0781 (效率 92.8%，可增加产出 7.81%)
Hospital J: 1.0963 (效率 91.2%，可增加产出 9.63%)

【输出导向CCR模型效率得分（CRS）】
模型特点：常数规模报酬，测量整体技术效率
------------------------------------------------------------
Hospital A: 1.2059 (效率 82.9%，可增加产出 20.59%)
Hospital B: 1.5375 (效率 65.0%，可增加产出 53.75%)
Hospital C: 1.0000 (效率前沿，效率 100%)
Hospital D: 1.1667 (效率 85.7%，可增加产出 16.67%)
Hospital E: 1.4455 (效率 69.2%，可增加产出 44.55%)
Hospital F: 1.1818 (效率 84.6%，可增加产出 18.18%)
Hospital G: 1.0000 (效率前沿，效率 100%)
Hospital H: 1.2308 (效率 81.2%，可增加产出 23.08%)
Hospital I: 1.3647 (效率 73.3%，可增加产出 36.47%)
Hospital J: 1.3000 (效率 76.9%，可增加产出 30.00%)

【模型间对比分析】
DMU          输入导向(BCC)       输入导向(CCR)       输出导向(BCC)       输出导向(CCR)       效率一致性     
-----------------------------------------------------------------------------------------------
Hospital A   0.8500          0.8293          1.0408          1.2059          不一致       
Hospital B   0.6667          0.6504          1.1206          1.5375          一致        
Hospital C   1.0000          1.0000          1.0000          1.0000          一致        
Hospital D   1.0000          0.8571          1.0000          1.1667          一致        
Hospital E   0.7273          0.6918          1.1403          1.4455          一致        
Hospital F   0.9487          0.8462          1.0144          1.1818          不一致       
Hospital G   1.0000          1.0000          1.0000          1.0000          一致        
Hospital H   1.0000          0.8125          1.0000          1.2308          一致        
Hospital I   0.7328          0.7328          1.0781          1.3647          一致        
Hospital J   0.7692          0.7692          1.0963          1.3000          一致        

【效率一致性详细分析】
一致性判断标准：
- 基于BCC模型（纯技术效率）比较输入导向和输出导向的结果
- 输入导向高效(≥0.99)且输出导向高效(≤1.05) = 一致高效
- 输入导向低效(<0.99)且输出导向低效(>1.05) = 一致低效
- 一个方向高效，另一个方向低效 = 不一致
----------------------------------------------------------------------
Hospital A: 不一致
Hospital B: 一致低效
Hospital C: 一致高效
Hospital D: 一致高效
Hospital E: 一致低效
Hospital F: 不一致
Hospital G: 一致高效
Hospital H: 一致高效
Hospital I: 一致低效
Hospital J: 一致低效

一致性摘要：8/10 个DMU在两个方向上表现一致

【统计摘要】
- BCC输出导向：平均得分 1.0491，6个DMU达到效率前沿
- CCR输出导向：平均得分 1.2433，2个DMU达到效率前沿
- 标准差：BCC输出导向 0.0524，CCR输出导向 0.1658

4. 运行规模效率分析...

================================================================================
规模效率分析 (Scale Efficiency Analysis)
================================================================================

规模效率分析说明：
- 技术效率(TE) = CCR得分
- 纯技术效率(PTE) = BCC得分
- 规模效率(SE) = TE / PTE = CCR得分 / BCC得分
- SE = 1 表示最优规模，SE < 1 表示规模无效率

规模效率分析结果:
DMU          技术效率       纯技术效率        规模效率       规模状态      
-----------------------------------------------------------------
Hospital A   0.8293     0.8500       0.9756     规模无效      
Hospital B   0.6504     0.6667       0.9756     规模无效      
Hospital C   1.0000     1.0000       1.0000     最优规模      
Hospital D   0.8571     1.0000       0.8571     规模无效      
Hospital E   0.6918     0.7273       0.9512     规模无效      
Hospital F   0.8462     0.9487       0.8919     规模无效      
Hospital G   1.0000     1.0000       1.0000     最优规模      
Hospital H   0.8125     1.0000       0.8125     规模无效      
Hospital I   0.7328     0.7328       1.0000     最优规模      
Hospital J   0.7692     0.7692       1.0000     最优规模      

规模效率摘要：
- 最优规模DMU数量: 4
- 平均规模效率: 0.9464
- 规模效率标准差: 0.0649

5. 运行Malmquist生产力分析...

================================================================================
Malmquist生产力指数分析 (Malmquist Productivity Index)
================================================================================

Malmquist指数分析说明：
- 测量两个时期之间的生产力变化
- MI > 1: 生产力提高
- MI = 1: 生产力不变
- MI < 1: 生产力下降
- 可以分解为技术效率变化和技术进步

2023年到2024年的生产力变化分析:
DMU          2023效率     2024效率     效率变化       Malmquist指数  状态        
---------------------------------------------------------------------------
Hospital A   0.8293     0.8286     0.9992     0.9546       生产力稳定     
Hospital B   0.6504     0.6560     1.0086     1.0776       生产力提高     
Hospital C   1.0000     0.9942     0.9942     1.1290       生产力提高     
Hospital D   0.8571     0.8750     1.0208     1.0461       生产力稳定     
Hospital E   0.6918     0.6957     1.0056     0.8167       生产力下降     
Hospital F   0.8462     0.8578     1.0138     1.0519       生产力提高     
Hospital G   1.0000     1.0000     1.0000     0.8718       生产力下降     
Hospital H   0.8125     0.8300     1.0215     1.0035       生产力稳定     
Hospital I   0.7328     0.7389     1.0084     1.1973       生产力提高     
Hospital J   0.7692     0.7636     0.9927     0.8927       生产力下降     

整体生产力变化摘要：
- 平均Malmquist指数: 1.0041
- 生产力提高的DMU数量: 4
- 生产力下降的DMU数量: 3
- 生产力稳定的DMU数量: 3

6. 运行综合比较分析...

================================================================================
四种DEA模型综合比较分析
================================================================================

📊 四种模型结果对比表
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
DMU          CCR输入      CCR输出      BCC输入      BCC输出      规模效率      
------------------------------------------------------------------------------------------
Hospital A   0.8293     1.2059     0.8500     1.0408     0.9756    
Hospital B   0.6504     1.5375     0.6667     1.1206     0.9756    
Hospital C   1.0000     1.0000     1.0000     1.0000     1.0000    
Hospital D   0.8571     1.1667     1.0000     1.0000     0.8571    
Hospital E   0.6918     1.4455     0.7273     1.1403     0.9512    
Hospital F   0.8462     1.1818     0.9487     1.0144     0.8919    
Hospital G   1.0000     1.0000     1.0000     1.0000     1.0000    
Hospital H   0.8125     1.2308     1.0000     1.0000     0.8125    
Hospital I   0.7328     1.3647     0.7328     1.0781     1.0000    
Hospital J   0.7692     1.3000     0.7692     1.0963     1.0000    

📈 效率前沿DMU数量统计
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
CCR输入导向: 2/10 (20.0%)
CCR输出导向: 2/10 (20.0%)
BCC输入导向: 4/10 (40.0%)
BCC输出导向: 6/10 (60.0%)

📊 平均效率得分
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
CCR输入导向: 0.8189
CCR输出导向: 1.2433
BCC输入导向: 0.8695
BCC输出导向: 1.0491

🎯 效率类型分析
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Hospital A: 需要改进
Hospital B: 需要改进
Hospital C: CCR高效, BCC高效, 规模最优
Hospital D: BCC高效
Hospital E: 需要改进
Hospital F: 需要改进
Hospital G: CCR高效, BCC高效, 规模最优
Hospital H: BCC高效
Hospital I: 规模最优
Hospital J: 规模最优

7. 生成综合分析图表...

Enhanced chart saved as 'dea_enhanced_efficiency_analysis.png'

================================================================================
DEA分析完成！
================================================================================

RSR 秩和比综合评价方法

秩和比法（Rank Sum Ratio, RSR） 是一种结合了非参数统计和多元统计思想的综合评价方法。该方法由中国统计学家田凤调教授于1988年提出，其核心思想是通过秩转换，将多个具有不同量纲、不同性质的评价指标转化为无量纲的秩和比值，从而对评价对象进行排序、分档和综合评估

RSR方法的基础是统计学中的“秩”（Rank）。秩代表一个数值在其所在数据序列中的相对位置。例如，在一组成绩 [65, 92, 78, 85] 中，92分是最高的，其秩为4；65分是最低的，其秩为1

RSR法正是利用了秩的这一特性：

剥离量纲：无论原始指标是“元”、“百分比”还是“个”，一旦转化为秩，它们都变成了统一的、无量纲的序号，从而具有了可比性
综合评价：通过将一个评价对象在所有指标下的秩次相加，可以得到一个总的“秩和”。这个秩和的大小，直观地反映了该对象在所有评价维度下的综合优劣程度
归一化处理：将秩和除以理论上的最大可能秩和，得到最终的RSR值，使其落在 (0, 1) 区间内，便于比较和理解。RSR值越接近1，表示综合评价越优

核心步骤

1. 构建原始数据矩阵并明确指标类型

将 $n$ 个评价对象和 $m$ 个评价指标整理成一个 $n \times m$ 的原始数据表

X = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{pmatrix}

同时，必须明确每个指标的属性：

高优指标（效益型）：指标值越大越好。如：GDP增长率、治愈率
低优指标（成本型）：指标值越小越好。如：死亡率、污染指数
中间值指标（适度型）：指标值越接近某个理想值或理想区间越好。如：学生体质指数（BMI）、水质酸碱度（pH）

2. 编秩（Ranking）

这是RSR方法最关键的一步，目的是将原始数据矩阵 $X$ 转换为秩次矩阵 $R$ 。编秩的规则取决于指标类型

高优指标：将原始数据从小到大排序，数值最小的秩为1，次小的为2，…，最大的为 $n$
低优指标：将原始数据从大到小排序，数值最大的秩为1，次大的为2，…，最小的为 $n$
中间值指标：
1. 确定最佳值/区间：首先确定一个最佳值 $M$ 或最佳区间 $[a, b]$
2. 计算离差：计算每个数据点与最佳值/区间的差距，生成一个新的“离差”序列
  - 最佳值：离差 $D_i = |X_i - M|$
  - 最佳区间：若 $X_i \in [a, b]$ , $D_i = 0$ ；若 $X_i < a$ , $D_i = a - X_i$ ；若 $X_i > b$ , $D_i = X_i - b$
3. 转化与编秩：这个“离差”序列是一个典型的低优指标（离差越小越好），因此对其按照低优指标的规则进行编秩
处理相同数值（结）：若一个指标下有多个相同数值，它们应获得其对应秩次的平均值。例如，某列数据从小到大排，第3、4、5位都是相同的值，则它们的秩次均为 $(3+4+5)/3 = 4$

3. 计算秩和比（RSR）

对每个评价对象，将其在所有指标下的秩次相加，然后进行归一化处理，得到该对象的RSR值

RSR_i = \frac{\sum_{j=1}^{m} R_{ij}}{n \times m}

其中：

$RSR_i$ 是第 $i$ 个评价对象的秩和比值
$\sum_{j=1}^{m} R_{ij}$ 是第 $i$ 个评价对象在 $m$ 个指标下的秩次之和
$n$ 是评价对象的总数
$m$ 是评价指标的总数

计算出的 $RSR_i$ 值介于 $(0, 1)$ 之间。可以直接根据RSR值的大小对所有评价对象进行排序，RSR值越大，综合评价结果越优

4.确定RSR的分布并计算概率单位（Probit）

可以通过了解RSR值的分布特征进行更客观的分档

排序：将计算出的所有 $RSR_i$ 值从小到大排序
计算平均秩次：对排序后的结果再次进行编制得到其平均秩次
计算累计频率 (Cumulative Frequency)： $P_i = \frac{\text{平均秩次}_i}{n} \times 100\%$ 。对于最后一个RSR值，为避免频率为100%导致概率单位无穷大，通常采用修正公式，如 $P_i = \frac{\text{平均秩次}_i}{n+1}$
转换为概率单位 (Probit)：将累计频率 $P_i$ 转换为标准正态分布对应的分位数，即Probit值。Probit是期望值为5、标准差为1的正态分布分位数（Probit = Z-score + 5）

5. 计算线性回归方程

以RSR值为因变量（Y），以其对应的概率单位Probit值为自变量（X），建立线性回归模型：

\hat{RSR} = a + b \times \text{Probit}

其中 $a$ 是截距， $b$ 是回归系数。这个回归方程描述了RSR值与正态分布分位数之间的线性关系，可以用来预测在特定概率水平下的RSR值。

6. 排序与分档（Stratified Grouping）

根据回归方程和预设的分档标准（通常依据概率单位），对评价对象进行等级划分

一个常用的分档标准是：

差 (Poor)：Probit < 4 (对应累计频率 < 15.87%)
中 (Medium)：4 ≤ Probit < 6 (对应累计频率 15.87% ~ 84.13%)
优 (Good)：Probit ≥ 6 (对应累计频率 > 84.13%)

将这些Probit分界值（如4和6）代入上一步计算出的回归方程，即可得到对应的RSR分档阈值，从而对所有评价对象进行科学、客观的等级划分。

优缺点分析

优点

适用性广：作为非参数方法，对数据类型和分布没有严格限制，稳健性好
操作简便：原理直观，计算步骤清晰，易于通过软件实现自动化
信息损失相对可控：虽然损失了原始数值的绝对大小信息，但保留了其相对位置（顺序）信息，这在很多综合评价场景中已经足够
结果客观：整个过程基于数据驱动，避免了主观赋权的困难和争议
支持深度分析：不仅提供排序，还能通过概率分档实现对评价对象的分类管理

缺点

信息损失：编秩过程会损失原始数据的绝对数值差异信息。例如，[90, 89] 和 [90, 60] 在编秩后可能得到完全相同的秩次，无法体现两者差距的悬殊
指标权重问题：传统RSR法默认所有指标同等重要。在实际应用中，若指标重要性不同，需要先用其他方法（如层次分析法AHP、熵权法等）确定权重，再计算加权秩和比（WRSR）。公式为： $WRSR_i = \frac{\sum_{j=1}^{m} (w_j \times R_{ij})}{n}$
区分度问题：当评价对象数量 $n$ 较少时，秩次的取值范围有限，可能导致RSR值的区分度不高

示例代码

假设需要对5个城市的综合发展水平进行评价，选取了3个指标：

X1: 人均GDP（万元） - 高优指标
X2: 空气优良率（%） - 高优指标
X3: 建成区绿地率（%） - 理想值为40%，中间值指标

# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
from scipy.stats import norm


class RankSumRatioEvaluator:
    """
    秩和比（Rank Sum Ratio, RSR）综合评价器

    该类将RSR方法的完整流程封装起来，支持极大、极小、中间、区间四种指标类型，
    并可选择性地进行加权计算（WRSR），最终实现对评价对象的排序和科学分档。
    此版本会详细打印每一步的中间计算结果，便于调试和过程展示。

    使用流程:
    1. 准备数据 (pd.DataFrame)。
    2. 定义指标配置 (dict)。
    3. (可选) 定义权重 (dict)。
    4. 创建类实例。
    5. 调用 evaluate() 方法获取最终结果。
    """

    def __init__(self, data_df, config, weights=None):
        """
        初始化评价器

        Args:
            data_df (pd.DataFrame): 原始数据，行应为评价对象，列为评价指标。
            config (dict): 指标配置字典。格式如下:
                {
                    '指标名1': {'type': 'high'},
                    '指标名2': {'type': 'low'},
                    '指标名3': {'type': 'middle', 'optimal': 理想值},
                    '指标名4': {'type': 'interval', 'optimal': [下限, 上限]}
                }
            weights (dict, optional): 指标权重字典，key为指标名，value为权重值。
                                      若为None，则所有指标等权重处理。默认为 None。
        """
        if not isinstance(data_df, pd.DataFrame):
            raise ValueError("输入数据 data_df 必须是 pandas DataFrame 格式。")
        if not data_df.index.is_unique:
            raise ValueError("数据框的索引（评价对象名称）必须是唯一的。")

        self.raw_data = data_df.copy()
        self.config = config
        self.n_samples, self.n_indicators = self.raw_data.shape
        self.weights = self._validate_weights(weights)
        self.results = self.raw_data.copy()

    def _validate_weights(self, weights):
        """验证权重的有效性"""
        if weights is None:
            # 如果不提供权重，则默认为等权重
            equal_weight = 1 / self.raw_data.shape[1]
            return {col: equal_weight for col in self.raw_data.columns}

        if not isinstance(weights, dict):
            raise ValueError("权重 'weights' 必须是一个字典。")

        # 检查权重是否覆盖所有指标且总和约等于1
        if set(weights.keys()) != set(self.raw_data.columns):
            raise ValueError("权重的键必须与数据框的列完全匹配。")
        if not np.isclose(sum(weights.values()), 1.0):
            print(f"警告: 权重之和为 {sum(weights.values()):.4f}，不严格等于1。请检查。")

        return weights

    def _rank_indicators(self):
        """核心步骤：根据指标类型进行编秩"""
        self.rank_matrix = pd.DataFrame(index=self.raw_data.index)
        self.deviation_matrix = pd.DataFrame(index=self.raw_data.index)

        for col_name, params in self.config.items():
            col_data = self.raw_data[col_name]
            indicator_type = params.get('type')

            if indicator_type == 'high':
                self.rank_matrix[col_name] = col_data.rank(method='average', ascending=True)

            elif indicator_type == 'low':
                self.rank_matrix[col_name] = col_data.rank(method='average', ascending=False)

            elif indicator_type == 'middle':
                optimal_value = params.get('optimal')
                if optimal_value is None:
                    raise ValueError(f"中间型指标 '{col_name}' 未在配置中提供 'optimal' 值。")
                deviation = abs(col_data - optimal_value)
                self.deviation_matrix[col_name + '_dev'] = deviation  # 存储离差值
                self.rank_matrix[col_name] = deviation.rank(method='average', ascending=False)

            elif indicator_type == 'interval':
                optimal_interval = params.get('optimal')
                if not (isinstance(optimal_interval, list) and len(optimal_interval) == 2):
                    raise ValueError(f"区间型指标 '{col_name}' 的 'optimal' 值必须是 [下限, 上限] 格式的列表。")

                low_bound, up_bound = optimal_interval
                deviation = col_data.apply(
                    lambda x: 0 if low_bound <= x <= up_bound else min(abs(x - low_bound), abs(x - up_bound))
                )
                self.deviation_matrix[col_name + '_dev'] = deviation  # 存储离差值
                self.rank_matrix[col_name] = deviation.rank(method='average', ascending=False)

            else:
                raise ValueError(f"指标 '{col_name}' 的类型 '{indicator_type}' 未知。")

    def _calculate_rsr(self):
        """计算秩和比(RSR)或加权秩和比(WRSR)"""
        weight_vector = pd.Series(self.weights)
        aligned_weights = weight_vector[self.rank_matrix.columns]

        weighted_rank_sum = self.rank_matrix.dot(aligned_weights)

        self.results['RSR'] = weighted_rank_sum / self.n_samples

    def _analyze_distribution(self):
        """计算RSR的分布，包括秩次、累计频率和概率单位Probit"""
        self.results = self.results.sort_values(by='RSR')
        self.results['RSR_Rank'] = self.results['RSR'].rank(method='average')
        self.results['Cum_Freq'] = self.results['RSR_Rank'] / (self.n_samples + 1)
        self.results['Probit'] = norm.ppf(self.results['Cum_Freq']) + 5

    def _fit_regression_and_group(self, probit_thresholds={'差': 4, '中': 6}):
        """拟合回归方程并进行分档"""
        valid_data = self.results.dropna(subset=['RSR', 'Probit'])
        valid_data = valid_data[np.isfinite(valid_data['Probit'])]

        if len(valid_data) < 2:
            self.results['Grouping'] = 'N/A'
            self.regression_eq = "N/A"
            self.rsr_thresholds = {}
            return

        probit_values = valid_data['Probit']
        rsr_values = valid_data['RSR']

        b, a = np.polyfit(probit_values, rsr_values, 1)
        self.regression_eq = f"RSR = {a:.4f} + {b:.4f} * Probit"

        self.rsr_thresholds = {}
        sorted_thresholds = sorted(probit_thresholds.items(), key=lambda item: item[1])
        for level, probit_val in sorted_thresholds:
            self.rsr_thresholds[level] = a + b * probit_val

        def classify(rsr_value):
            if rsr_value >= self.rsr_thresholds['中']:
                return '优'
            elif rsr_value >= self.rsr_thresholds['差']:
                return '中'
            else:
                return '差'

        self.results['Grouping'] = self.results['RSR'].apply(classify)

    def evaluate(self):
        """
        执行完整的RSR评价流程，并打印所有中间结果。

        Returns:
            pd.DataFrame: 一个包含所有中间和最终结果的DataFrame。
        """
        print("--- 开始秩和比(RSR)评价 ---")
        use_weighted = not np.allclose(list(self.weights.values()), 1 / self.n_indicators)
        if use_weighted:
            print("模式: 加权秩和比 (WRSR)")
            print("权重:", self.weights)
        else:
            print("模式: 等权重秩和比 (RSR)")

        # 步骤1: 编秩
        print("\n[1/5] 正在根据指标类型进行编秩...")
        self._rank_indicators()
        if not self.deviation_matrix.empty:
            print("\n--- 中间结果: 离差矩阵 (仅对中间/区间型指标) ---")
            print(self.deviation_matrix)
        print("\n--- 中间结果: 完整秩次矩阵 ---")
        print(self.rank_matrix)

        # 步骤2: 计算RSR
        print("\n[2/5] 正在计算RSR值...")
        self._calculate_rsr()
        print("\n--- 中间结果: 计算RSR后的数据表 ---")
        print(self.results[['RSR']].sort_values(by='RSR'))

        # 步骤3: 确定分布
        print("\n[3/5] 正在分析RSR分布并计算Probit值...")
        self._analyze_distribution()
        print("\n--- 中间结果: RSR分布特征分析表 ---")
        print(self.results[['RSR', 'RSR_Rank', 'Cum_Freq', 'Probit']])

        # 步骤4: 回归
        print("\n[4/5] 正在拟合回归模型...")
        self._fit_regression_and_group()
        print("\n--- 中间结果: 回归分析与分档阈值 ---")
        print(f"拟合回归方程: {self.regression_eq}")
        print("计算出的RSR分档线:", {k: round(v, 4) for k, v in self.rsr_thresholds.items()})

        # 步骤5: 最终结果
        print("\n[5/5] 正在生成最终报告...")
        final_results = self.results.reindex(self.raw_data.index)

        print("\n--- RSR评价完成 ---")
        return final_results


if __name__ == '__main__':
    # 1. 准备原始数据 (例如，评价8个地区的发展状况)
    data = {
        '地区': [f'地区{chr(65 + i)}' for i in range(8)],
        '人均GDP(万元)': [18, 12, 22, 10, 15, 19, 11, 14],  # 极大值
        '新生儿死亡率(‰)': [3.5, 4.8, 2.1, 5.5, 4.1, 3.1, 5.2, 4.5],  # 极小值
        '师生比(1:X)': [15, 18, 14, 20, 16, 15.5, 19, 17],  # 中间值，理想为1:15
        '空气优良天数比例(%)': [85, 92, 88, 75, 95, 98, 82, 78],  # 区间值，理想范围[85, 95]
    }
    df_raw = pd.DataFrame(data).set_index('地区')

    # 2. 定义指标配置
    config_demo = {
        '人均GDP(万元)': {'type': 'high'},
        '新生儿死亡率(‰)': {'type': 'low'},
        '师生比(1:X)': {'type': 'middle', 'optimal': 15},
        '空气优良天数比例(%)': {'type': 'interval', 'optimal': [85, 95]},
    }

    # 3. (可选) 定义权重 - 如果不定义，则每个指标权重为 1/4 = 0.25
    weights_demo = {
        '人均GDP(万元)': 0.35,
        '新生儿死亡率(‰)': 0.35,
        '师生比(1:X)': 0.15,
        '空气优良天数比例(%)': 0.15,
    }

    print("=" * 20 + " 案例一: 加权秩和比评价 " + "=" * 20)
    # 4. 创建实例并执行评价 (使用加权)
    evaluator_weighted = RankSumRatioEvaluator(df_raw, config_demo, weights=weights_demo)
    final_report_weighted = evaluator_weighted.evaluate()

    # 5. 显示最终报告
    print("\n\n=============== 最终综合评价报告 (加权) ================")
    print(final_report_weighted)

学习笔记

#数学建模

数模笔记模型篇一

https://blog.giraffish.me/post/51e2c075/

作者

卖柠檬雪糕的鱼

发布于

2025年5月31日

更新于

2025年7月18日

许可协议

数模笔记基础篇上一篇

机器学习笔记下一篇