CS203 Data Structure and Algorithm Analysis

部分笔记摘录自hello-algo

栈 & 队列

双向队列

/* 基于环形数组实现的双向队列 */
class ArrayDeque {
    private int[] nums; // 用于存储双向队列元素的数组
    private int front; // 队首指针，指向队首元素
    private int queSize; // 双向队列长度

    /* 构造方法 */
    public ArrayDeque(int capacity) {
        this.nums = new int[capacity];
        front = queSize = 0;
    }

    /* 获取双向队列的容量 */
    public int capacity() {
        return nums.length;
    }

    /* 获取双向队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    public boolean isEmpty() {
        return queSize == 0;
    }

    /* 计算环形数组索引 */
    private int index(int i) {
        // 通过取余操作实现数组首尾相连
        // 当 i 越过数组尾部后，回到头部
        // 当 i 越过数组头部后，回到尾部
        return (i + capacity()) % capacity();
    }

    /* 队首入队 */
    public void pushFirst(int num) {
        if (queSize == capacity()) {
            System.out.println("双向队列已满");
            return;
        }
        // 队首指针向左移动一位
        // 通过取余操作实现 front 越过数组头部后回到尾部
        front = index(front - 1);
        // 将 num 添加至队首
        nums[front] = num;
        queSize++;
    }

    /* 队尾入队 */
    public void pushLast(int num) {
        if (queSize == capacity()) {
            System.out.println("双向队列已满");
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        int rear = index(front + queSize);
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 队首出队 */
    public int popFirst() {
        int num = peekFirst();
        // 队首指针向后移动一位
        front = index(front + 1);
        queSize--;
        return num;
    }

    /* 队尾出队 */
    public int popLast() {
        int num = peekLast();
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    public int peekFirst() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return nums[front];
    }

    /* 访问队尾元素 */
    public int peekLast() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        // 计算尾元素索引
        int last = index(front + queSize - 1);
        return nums[last];
    }

    /* 返回数组用于打印 */
    public int[] toArray() {
        // 仅转换有效长度范围内的列表元素
        int[] res = new int[queSize];
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[index(j)];
        }
        return res;
    }
}

树

二叉树

/* 二叉树节点类 */
class TreeNode {
    int val;         // 节点值
    TreeNode left;   // 左子节点引用
    TreeNode right;  // 右子节点引用
    TreeNode(int x) { val = x; }
}

层序遍历（BFS）

/* 层序遍历 */
List<Integer> levelOrder(TreeNode root) {
    // 初始化队列，加入根节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    // 初始化一个列表，用于保存遍历序列
    List<Integer> list = new ArrayList<>();
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // 队列出队
        list.add(node.val);           // 保存节点值
        if (node.left != null)
            queue.offer(node.left);   // 左子节点入队
        if (node.right != null)
            queue.offer(node.right);  // 右子节点入队
    }
    return list;
}

前序/中序/后续遍历（DFS）

/* 前序遍历 */
void preOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：根节点 -> 左子树 -> 右子树
    list.add(root.val);
    preOrder(root.left);
    preOrder(root.right);
}

/* 中序遍历 */
void inOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 根节点 -> 右子树
    inOrder(root.left);
    list.add(root.val);
    inOrder(root.right);
}

/* 后序遍历 */
void postOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 右子树 -> 根节点
    postOrder(root.left);
    postOrder(root.right);
    list.add(root.val);
}

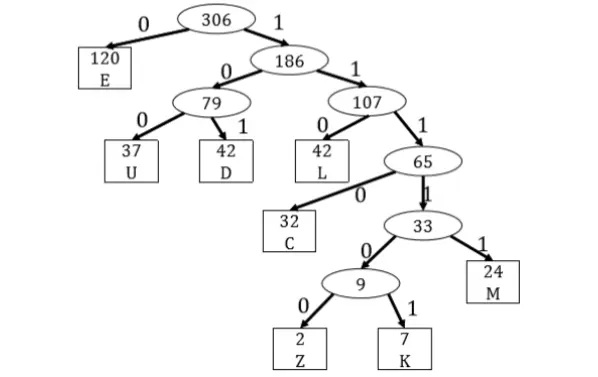
哈夫曼编码

伪代码：

函数 HuffmanCoding(字符集 C):
    n = |C|
    Q = 优先队列(按频率升序)

    # 1. 初始化队列
    对于 C 中的每个字符 c:
        创建一个节点 z
        z.字符 = c
        z.频率 = c.频率
        Insert(Q, z)

    # 2. 构建哈夫曼树
    当 Q.size > 1 时执行:
        # 取出两个最小的
        x = ExtractMin(Q)
        y = ExtractMin(Q)

        # 合并为一个新节点
        z = 新节点()
        z.left = x
        z.right = y
        z.频率 = x.频率 + y.频率
        
        # 将新节点放回队列
        Insert(Q, z)

    # 3. 返回根节点
    Return ExtractMin(Q)

函数 GenerateCodes(节点 node, 当前编码 code):
    如果 node 是叶子节点:
        打印/存储 node.字符 : code
        返回
    
    GenerateCodes(node.left, code + "0")
    GenerateCodes(node.right, code + "1")

BST

https://www.hello-algo.com/chapter_tree/binary_search_tree/

前序查找

时间复杂度 O(h)

public long predecessorQuery(Node root, long q) {
	//节点为空
	if (root == null) {
		return -1;
	//二叉搜索树中存在key=q的节点
	} else if (root.element == q) {
		return root.element;
	//当前节点的key>q的时候，将左子节点(更小)作为查询root节点
	} else if (root.element > q) {
		return predecessorQuery(root.leftChild, q);
	//当前节点的key<q的时候，保存当前的节点的key，将右子节点(更大)作为查询root节点，并且返回的key与当前节点的key做对比，如果是为-1证明无法找到
	} else {
		long temp = predecessorQuery(root.rightChild, q);
		if (temp == -1) {
			return root.element;
		} else {
		return temp;
		}
	}
}

后序查找

时间复杂度 O(h)

public long successorQuery(Node root, long q) {
	if (root == null) {
		return -1;
	} else if (root.element == q) {
		return root.element;
	} else if (root.element > q) {
		long temp = successorQuery(root.leftChild, q);
		if (temp == -1) {
			return root.element;
		} else {
			return temp;
		}
	} else {
		return successorQuery(root.rightChild, q);
	}
}

AVL

https://www.hello-algo.com/chapter_tree/avl_tree/

策略表：

失衡节点的平衡因子	子节点的平衡因子	应采用的旋转方法
$> 1$ （左偏树）	$\geq 0$	右旋
$> 1$ （左偏树）	$<0$	先左旋后右旋
$< -1$ （右偏树）	$\leq 0$	左旋
$< -1$ （右偏树）	$>0$	先右旋后左旋

堆

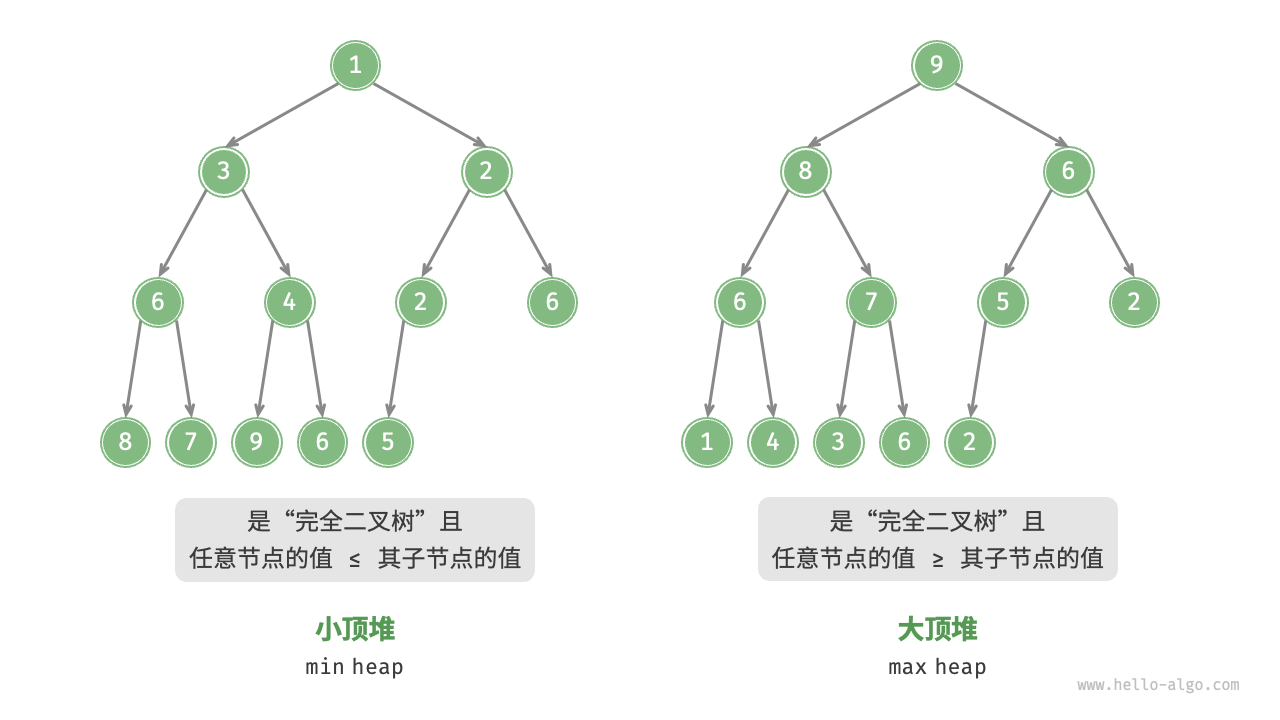
堆（heap）是一种满足特定条件的完全二叉树，主要可分为两种类型，如下图所示。

• 小顶堆（min heap）：任意节点的值 $\leq$ 其子节点的值
• 大顶堆（max heap）：任意节点的值 $\geq$ 其子节点的值

下文实现的是大顶堆，若要将其转换为小顶堆，只需将所有大小逻辑判断进行逆转（例如，将 $\geq$ 替换为 $\leq$ ）

堆的存储与表示

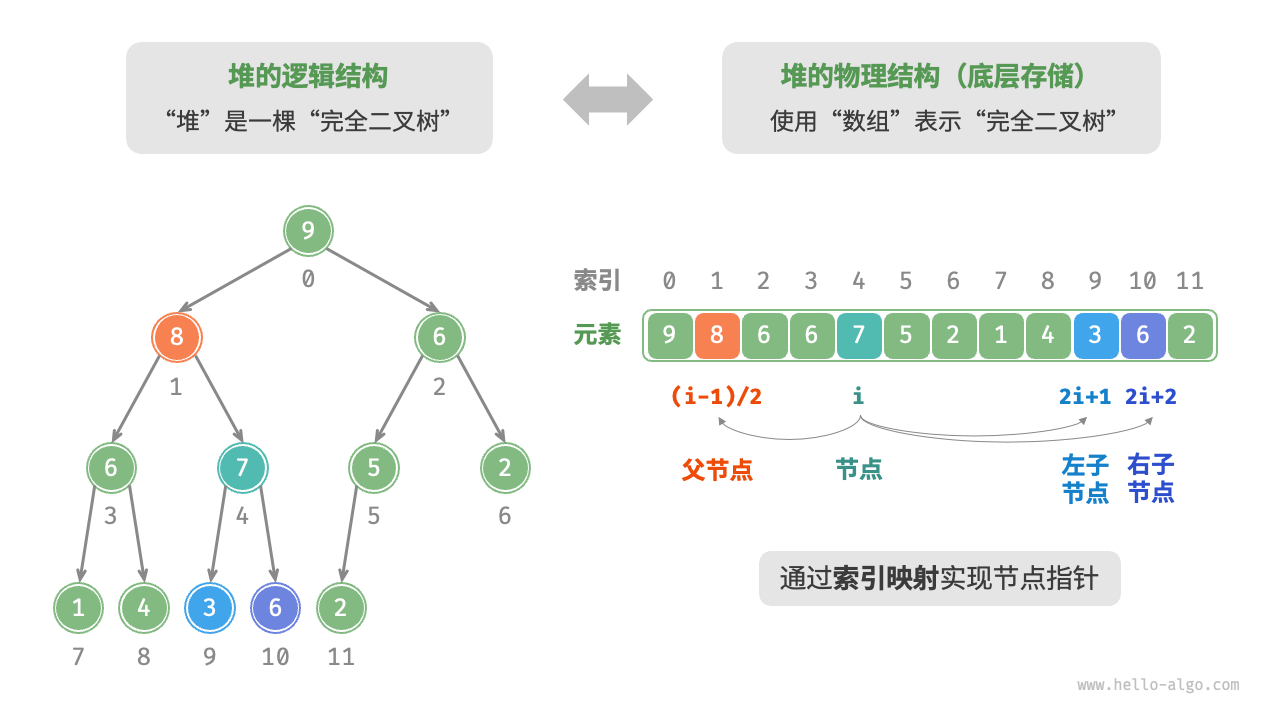
“二叉树”章节讲过，完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树，因此我们将采用数组来存储堆。

当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。

如下图所示，给定索引 $i$ ，其左子节点的索引为 $2i + 1$ ，右子节点的索引为 $2i + 2$ ，父节点的索引为 $(i - 1) / 2$（向下整除）。当索引越界时，表示空节点或节点不存在

堆的操作

元素入堆

时间复杂度为 $O(\log n)$

/* 元素入堆 */
void push(int val) {
    // 添加节点
    maxHeap.add(val);
    // 从底至顶堆化
    siftUp(size() - 1);
}

/* 从节点 i 开始，从底至顶堆化 */
void siftUp(int i) {
    while (true) {
        // 获取节点 i 的父节点
        int p = parent(i);
        // 当“越过根节点”或“节点无须修复”时，结束堆化
        if (p < 0 || maxHeap.get(i) <= maxHeap.get(p))
            break;
        // 交换两节点
        swap(i, p);
        // 循环向上堆化
        i = p;
    }
}

元素出堆

时间复杂度为 $O(\log n)$

/* 元素出堆 */
int pop() {
    // 判空处理
    if (isEmpty())
        throw new IndexOutOfBoundsException();
    // 交换根节点与最右叶节点（交换首元素与尾元素）
    swap(0, size() - 1);
    // 删除节点
    int val = maxHeap.remove(size() - 1);
    // 从顶至底堆化
    siftDown(0);
    // 返回堆顶元素
    return val;
}

/* 从节点 i 开始，从顶至底堆化 */
void siftDown(int i) {
    while (true) {
        // 判断节点 i, l, r 中值最大的节点，记为 ma
        int l = left(i), r = right(i), ma = i;
        if (l < size() && maxHeap.get(l) > maxHeap.get(ma))
            ma = l;
        if (r < size() && maxHeap.get(r) > maxHeap.get(ma))
            ma = r;
        // 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if (ma == i)
            break;
        // 交换两节点
        swap(i, ma);
        // 循环向下堆化
        i = ma;
    }
}

Root-fix 建堆

时间复杂度为 $O(n)$

证明如下：

假设树的高度为 $h$（即 $\log N$），总操作次数 $S$ 是每一层节点数乘以该层节点可能下沉的最大高度

• 倒数第 1 层（叶子）：$2^h$ 个节点，下沉 0 层。倒数第 2 层：$2^{h-1}$ 个节点，下沉 1 层。
• 倒数第 3 层：$2^{h-2}$ 个节点，下沉 2 层。
• …
• 根节点：$2^0$ 个节点，下沉 $h$ 层。

总工作量公式：

$$S = \sum_{i=0}^{h} 2^i \cdot (h-i) = 2^0 \cdot h + 2^1 \cdot (h-1) + \dots + 2^{h-1} \cdot 1$$

利用错位相减法求和，结果为：

$$S = 2^{h+1} - h - 2$$

因为 $N \approx 2^{h+1}$，所以：

$$S \approx N - \log N - 2$$

结论：

$$S = O(N)$$

MaxHeap(List<Integer> nums) {
    // 将列表元素原封不动添加进堆
    maxHeap = new ArrayList<>(nums);
    // 堆化除叶节点以外的其他所有节点，第一个最右边非叶子节点是最后一个节点的父节点
    for (int i = parent(size() - 1); i >= 0; i--) {
        siftDown(i);
    }
}

图

图（graph） 是一种非线性数据结构，由 顶点（vertex） 和 边（edge） 组成。我们可以将图 $G$ 抽象地表示为一组顶点 $V$ 和一组边 $E$ 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。

$$\begin{aligned} V & = \{ 1, 2, 3, 4, 5 \} \newline E & = \{ (1,2), (1,3), (1,5), (2,3), (2,4), (2,5), (4,5) \} \newline G & = \{ V, E \} \newline \end{aligned}$$

常见术语

• 有向图：directed graph，Unidirectional
• 无向图：Undirected Graph，Bidirectional
• 连通图（connected graph）：从某个顶点出发，可以到达其余任意顶点
• 非连通图（disconnected graph）：从某个顶点出发，至少有一个顶点无法到达
• 邻接（adjacency）：当两顶点之间存在边相连时
• 路径（path）：从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”
• 度（degree）：一个顶点拥有的边数。对于有向图，入度（in-degree） 表示有多少条边指向该顶点，出度（out-degree） 表示有多少条边从该顶点指出

图的表示

邻接矩阵

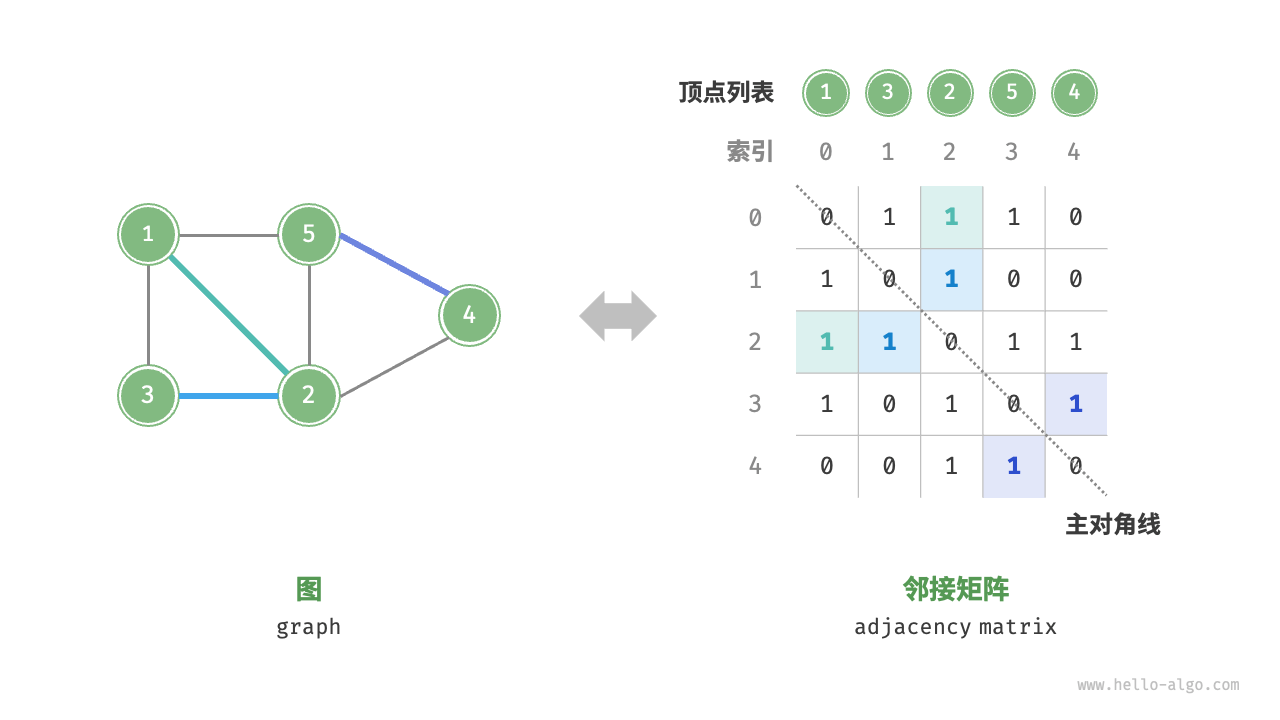
设图的顶点数量为 $n$ ，邻接矩阵（adjacency matrix） 使用一个 $n \times n$ 大小的矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 $1$ 或 $0$ 表示两个顶点之间是否存在边

如下图所示，设邻接矩阵为 $M$、顶点列表为 $V$ ，那么矩阵元素 $M[i, j] = 1$ 表示顶点 $V[i]$ 到顶点 $V[j]$ 之间存在边，反之 $M[i, j] = 0$ 表示两顶点之间无边

• 对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称
• 将邻接矩阵的元素从 $1$ 和 $0$ 替换为权重，则可表示有权图
• $Space = O(|V|^2)$

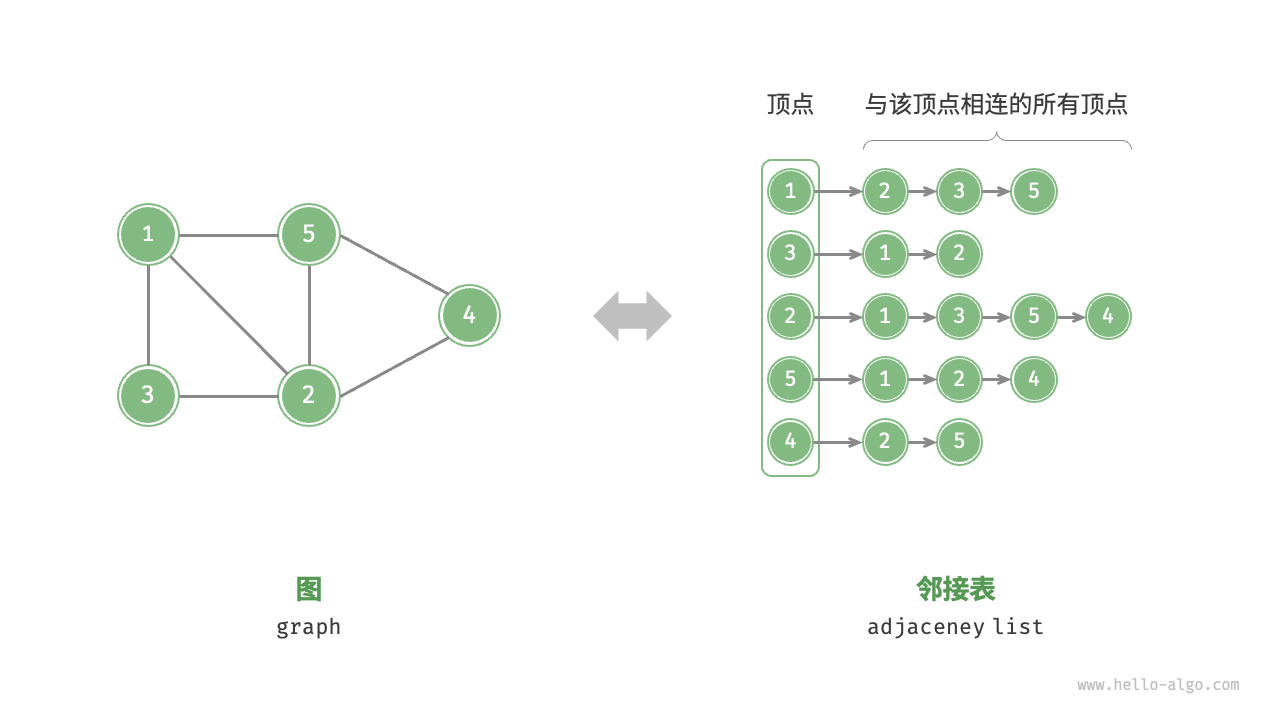
邻接表

邻接表（adjacency list） 使用 $n$ 个链表来表示图，链表节点表示顶点。第 $i$ 个链表对应顶点 $i$ ，其中存储了该顶点的所有邻接顶点（与该顶点相连的顶点）

邻接表仅存储实际存在的边，而边的总数通常远小于 $n^2$ ，$Space = O(|V|+|E|)$，因此它更加节省空间。然而，在邻接表中需要通过遍历链表来查找边，因此其时间效率不如邻接矩阵

观察上图，邻接表结构与哈希表中的“链式地址”非常相似，因此我们也可以采用类似的方法来优化效率。比如当链表较长时，可以将链表转化为 AVL 树或红黑树，从而将时间效率从 $O(n)$ 优化至 $O(\log n)$ ；还可以把链表转换为哈希表，从而将时间复杂度降至 $O(1)$

Java 示例代码：

import java.util.*;

class Graph {
    int V; // 顶点数
    ArrayList<Integer>[] adj; 

    // 构造函数
    public Graph(int V) {
        this.V = V;
        // 初始化邻接表数组
        adj = new ArrayList[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new ArrayList<>();
        }
    }

    // 添加边 u -> v
    public void addEdge(int u, int v) {
        adj[u].add(v);
    }
}

下面的Java示例沿用此代码模板

BFS 与 DFS

广度优先搜索 (BFS - Breadth-First Search)

BFS 就像是水波纹扩散或者剥洋葱。它从起点开始，先访问离起点最近的所有节点（第1层），然后再访问离起点稍远的所有节点（第2层），以此类推。核心数据结构：队列 (Queue)

伪代码：

BFS(Graph, StartNode):
    创建一个队列 Q
    创建一个集合 Visited 用于记录已访问节点
    
    Q.enqueue(StartNode)
    Visited.add(StartNode)
    
    WHILE Q is not empty:
        CurrentNode = Q.dequeue()
        PRINT CurrentNode
        
        FOR EACH Neighbor in Graph.neighbors(CurrentNode):
            IF Neighbor is NOT in Visited:
                Visited.add(Neighbor)
                Q.enqueue(Neighbor)

Java示例：

public static void bfs(Graph g, int startNode) {
    System.out.println("--- BFS 开始 (起点: " + startNode + ") ---");

    boolean[] visited = new boolean[g.V];
    LinkedList<Integer> queue = new LinkedList<>(); // 队列

    // 起点入队
    visited[startNode] = true;
    queue.add(startNode);

    while (!queue.isEmpty()) {
        // 1. 取出队头
        int curr = queue.poll();
        System.out.print(curr + " ");

        // 2. 遍历所有邻居
        for (int neighbor : g.adj[curr]) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                queue.add(neighbor);
            }
        }
    }
    System.out.println();
}

深度优先搜索 (DFS - Depth-First Search)

DFS 就像是走迷宫。它选择一条路一直走到黑（直到无路可走），然后回溯 (Backtrack) 到上一个路口，选择另一条没走过的路继续尝试。核心数据结构：栈 (Stack) (通常通过递归的系统栈实现，也可以手动用 Stack)

伪代码：

// 主函数
DFS(Graph):
    创建一个集合 Visited
    FOR EACH Node in Graph:
        IF Node is NOT in Visited:
            DFS_Recursive(Node, Visited)

// 递归辅助函数
DFS_Recursive(CurrentNode, Visited):
    Visited.add(CurrentNode)
    PRINT CurrentNode
    
    FOR EACH Neighbor in Graph.neighbors(CurrentNode):
        IF Neighbor is NOT in Visited:
            DFS_Recursive(Neighbor, Visited)

Java示例：

// 递归辅助函数
private static void dfsUtil(Graph g, int v, boolean[] visited) {
    // 1. 访问当前点
    visited[v] = true;
    System.out.print(v + " ");

    // 2. 递归访问所有未访问的邻居
    for (int neighbor : g.adj[v]) {
        if (!visited[neighbor]) {
            dfsUtil(g, neighbor, visited);
        }
    }
}

// 主函数
public static void dfs(Graph g, int startNode) {
    System.out.println("--- DFS 开始 (起点: " + startNode + ") ---");
    boolean[] visited = new boolean[g.V];
    dfsUtil(g, startNode, visited);
    System.out.println();
}

DAG 有向无环图

判断是否为DAG (Directed Acyclic Graph) 的经典方法有两种

• DFS (三色标记法)
• BFS (Kahn 算法 / 拓扑排序法)

DFS (三色标记法)

我们需要三个状态来区分“正在递归栈中”和“已经搜索完毕”

三种颜色（状态）：

• 0 (White/未访问)：还没走到这里
• 1 (Gray/正在访问)：正在这个节点的递归栈里（我在它的子孙节点中打转，还没回溯回来）。如果碰到了状态 1 的点，说明遇到了“回头路”，即有环！
• 2 (Black/已完成)：这个点及其所有子孙都遍历完了，没发现环

从任意点出发 DFS，如果你走着走着，看到了一个标为 1 (Gray) 的节点，说明你回到了祖先节点 $\to$ 有环

Java示例代码：

public static boolean hasCycle(int n, ArrayList<Integer>[] adj) {
        int[] state = new int[n]; // 0:未访问, 1:正在访问, 2:已完成
        
        // 图可能不是连通的，所以要遍历所有节点
        for (int i = 0; i < n; i++) {
            if (state[i] == 0) {
                if (dfsCheckCycle(i, adj, state)) {
                    return true; // 发现环
                }
            }
        }
        return false; // 没发现环，是 DAG
    }

    private static boolean dfsCheckCycle(int u, ArrayList<Integer>[] adj, int[] state) {
        // 1. 标记当前节点为 "正在访问" (入栈)
        state[u] = 1; 

        for (int v : adj[u]) {
            if (state[v] == 1) {
                // 核心判断：碰到了正在访问的祖先 -> 有环！
                return true; 
            }
            if (state[v] == 0) {
                // 继续深搜，如果有环直接向上传递 true
                if (dfsCheckCycle(v, adj, state)) {
                    return true;
                }
            }
            // 如果 state[v] == 2，说明那是条死胡同或者已经安全检查过了，跳过
        }

        // 2. 标记当前节点为 "已完成" (出栈)
        state[u] = 2; 
        return false;
    }

BFS (Kahn 算法 / 拓扑排序法)

这也是拓扑排序 (Topological Sort) 的核心逻辑

核心思路： DAG 的一个重要性质是：一定存在一个“入度为 0”的点（没有任何箭头指向它的点，即起跑线）

1. 找到所有 入度 (Indegree) 为 0 的点，把它们“删掉”（放入队列）
2. 当你删掉一个点时，它发出的箭头也随之消失，这可能会让它的邻居的入度变成 0
3. 重复这个过程
4. 结论：如果你能删光所有点，它就是 DAG。如果最后还剩下一堆点删不掉（因为它们互指，入度永远不为 0），那就是有环

Java示例代码：

public class TopologicalSort {

    // 输入：n 是节点数，adj 是邻接表
    // 输出：拓扑排序后的数组。如果图中有环，返回空数组。
    public static int[] getTopologicalSort(int n, ArrayList<Integer>[] adj) {
        
        // 1. 初始化入度数组 (Indegree)
        int[] inDegree = new int[n];
        for (int u = 0; u < n; u++) {
            for (int v : adj[u]) {
                inDegree[v]++;
            }
        }

        // 2. 将所有入度为 0 (无依赖) 的点放入队列
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                queue.add(i);
            }
        }

        // 结果数组
        int[] result = new int[n];
        int index = 0;

        // 3. BFS 拆解图
        while (!queue.isEmpty()) {
            int u = queue.poll();
            result[index++] = u; // 加入结果集

            // 遍历邻居，减少它们的入度
            for (int v : adj[u]) {
                inDegree[v]--; 
                // 如果 v 的依赖全部解决 (入度变0)，则加入队列
                if (inDegree[v] == 0) {
                    queue.add(v);
                }
            }
        }

        // 4. 检查是否有环
        // 如果结果集里的数量少于 n，说明剩下的点形成环，互为依赖，无法解开
        if (index != n) {
            return new int[0]; // 或者抛出异常
        }

        return result;
    }

Dijkstra 算法

Dijkstra 算法是一种用于在正权图中查找从单一源点到所有其他节点的最短路径的经典算法。它采用了贪心策略 (Greedy Strategy)，并被证明具有普遍最优性

伪代码：

function Dijkstra(G, s):
    // 1. 初始化 (Initialization)
    N ← G 中的节点数量
    
    // 初始化距离数组为无穷大，前驱数组为 null
    对于 i 从 1 到 N:
        dist[i]   ← infinity
        parent[i] ← null
    
    // 源点到自己的距离为 0
    dist[s] ← 0
    
    // 初始化最小堆，并将源点推入
    // 堆中元素格式：(当前距离, 节点编号)
    pq ← empty Min-Heap
    pq.push( (0, s) )

    // 2. 主循环 (Processing)
    当 pq 不为空时:
        // 弹出堆顶元素：距离源点最近的“未知”节点
        (d, u) ← pq.pop()

        // [关键优化：懒惰删除检查]
        // 如果从堆中弹出的距离 d 大于当前记录的最短距离 dist[u]，
        // 说明这是一个“过时”的记录（该节点已被通过更短的路径处理过），直接跳过。
        如果 d > dist[u]:
            continue

        // 3. 遍历邻居并松弛 (Traverse Neighbors & Relax)
        // 遍历 u 的所有出边 (u -> v)，权重为 w
        对于 (v, w) in G[u]:
            
            // 计算经由 u 到达 v 的新距离
            new_dist ← dist[u] + w

            // [松弛操作]
            // 如果找到更短的路径
            如果 new_dist < dist[v]:
                // 更新最短距离
                dist[v] ← new_dist
                
                // 记录前驱节点（用于回溯路径）
                parent[v] ← u
                
                // 将更新后的距离和节点推入堆中
                // 注意：旧的 (old_dist, v) 仍然在堆中，但在弹出时会被上方的“懒惰删除检查”过滤掉
                pq.push( (new_dist, v) )

    return dist, parent

Bellman-Ford 算法

Bellman-Ford (贝尔曼-福特) 也是一种用于在加权图中寻找单源最短路径 (Single-Source Shortest Path) 的经典算法，它不贪心但是可以处理负权图

Bellman-Ford 需要进行 V-1 轮松弛，每一轮松弛都要遍历所有边

伪代码：

function BellmanFord(G, s):
    // 1. 初始化 (Initialization)
    N ← G 中的节点数量
    
    // 初始化距离数组为无穷大，前驱数组为 null
    对于 i 从 1 到 N:
        dist[i]   ← infinity
        parent[i] ← null
    
    // 源点到自己的距离为 0
    dist[s] ← 0

    // 获取图中所有的边列表 (Edge List)
    // 形式为：(u, v, w) 表示从 u 到 v 权重为 w
    edges ← G.getAllEdges() 

    // 2. 连续松弛 N-1 轮 (Relaxation Phase)
    // 在没有任何负权环的图中，任意最短路径最多包含 N-1 条边。
    // 所以我们需要对所有边进行 N-1 轮松弛操作。
    重复 N-1 次:
        
        // 遍历图中的每一条边 (u, v, w)
        // 注意：这里必须遍历全图所有的边，而不只是像Dijkstra那样遍历当前最近节点的邻居
        对于每一条边 (u, v, w) in edges:
            
            // [松弛操作]
            // 前提：起点到 u 必须是可达的 (dist[u] != infinity)
            // 且经由 u 到 v 的距离更短
            如果 dist[u] != infinity 且 dist[u] + w < dist[v]:
                
                // 更新最短距离
                dist[v] ← dist[u] + w
                
                // 记录前驱节点
                parent[v] ← u

    // 3. 负权环检测 (Negative Cycle Detection)
    // 再遍历一次所有边。如果此时还能进行松弛，说明图中存在负权环。
    // 因为正常的最短路径在 N-1 轮后应该已经收敛固定了。
    has_negative_cycle ← false
    
    对于每一条边 (u, v, w) in edges:
        如果 dist[u] != infinity 且 dist[u] + w < dist[v]:
            has_negative_cycle ← true
            break // 发现负环，可以直接跳出

    // 4. 返回结果
    如果 has_negative_cycle 为 true:
        return "Error: Negative Weight Cycle Detected"
    否则:
        return dist, parent

Prim 算法

Prim 算法用于解决在加权连通图中寻找MST最小生成树，即找到连接图中所有顶点的一组边，使得这些边的总权重最小，且不形成任何环

Prim 算法与 Dijkstra 非常相似，主要区别在于：Dijkstra 关注的是从起点到当前节点的累积距离，而 Prim 关注的是当前节点连接到生成树的最小权重边

伪代码：

function Prim(G, s):
    // 1. 初始化 (Initialization)
    N ← G 中的节点数量
    
    // 【修改点 1：dist 的含义变了】
    // 在 Dijkstra 中，dist 代表“离起点的累积距离”
    // 在 Prim 中，dist 代表“离生成树的最小距离 (Cut value)”
    对于 i 从 1 到 N:
        dist[i]   ← infinity
        parent[i] ← null
    
    // 源点进入树的代价为 0
    dist[s] ← 0
    
    // 初始化最小堆
    pq ← empty Min-Heap
    pq.push( (0, s) )
    
    // [新增] 标记数组，用于判断节点是否已经加入了 MST
    // 虽然通过 lazy check 也能运作，但加上 visited 逻辑更严谨且能防止环
    inMST ← array of false 

    // 2. 主循环 (Processing)
    当 pq 不为空时:
        // 弹出堆顶元素：离“生成树”最近的节点
        (d, u) ← pq.pop()

        // [关键优化：懒惰删除检查]
        // 如果该节点已经在 MST 中（或者这是一个过时的更差权重记录），跳过
        如果 inMST[u] == true 或者 d > dist[u]:
            continue

        // 将 u 标记为正式加入 MST
        inMST[u] ← true

        // 3. 遍历邻居并更新 (Traverse Neighbors & Update)
        对于 (v, w) in G[u]:
            // 如果 v 已经在 MST 中，则不需要处理（防止成环）
            如果 inMST[v] == true:
                continue

            // 【修改点 2：核心逻辑变化】
            // Dijkstra: new_dist ← dist[u] + w  (我们要的是累积路径)
            // Prim:     new_dist ← w            (我们要的只是这条边的权重)
            
            // 如果这条边 (u, v) 的权重 w 小于 v 当前记录的“入树最小代价”
            如果 w < dist[v]:
                // 更新 v 的最小入树代价
                dist[v] ← w
                
                // 记录前驱节点（表明 v 是通过 u 连入树的）
                parent[v] ← u
                
                // 将更新后的代价和节点推入堆中
                pq.push( (w, v) )

    return dist, parent, (以及由 parent 构成的 MST 边集)

Kruskal 算法

Kruskal算法是图论中另一种寻找最小生成树 (MST) 的经典贪心算法，它不关心从哪个点开始，而是直接着眼于边，按照权重的从小到大，把边一条条加进来，直到所有点都连通

通过使用并查集来判断两个点是否已经连通，初始时每个点一个集合，在连通两点时合并两点属于的集合，从而根据两点是否属于一个集合来判断两点是否连通

Prim 算法适合稠密图（边很多），Kruskal 算法适合稀疏图（边较少）

伪代码：

Kruskal(G):
    // 1. 初始化结果边集A为空
    A = {}
    
    // 2. 初始化并查集：每个顶点自成一个集合
    FOR each vertex v IN G.V:
        Make_Set(v)

    // 3. 关键步骤：按权重对所有边进行升序排序
    Sort the edges E by weight in non-decreasing order

    // 4. 遍历排序后的边
    FOR each edge (u, v) IN E:
        // 如果 u 和 v 不在同一个集合中（即不形成环）
        IF Find_Set(u) != Find_Set(v):
            // 将这条边加入结果集
            A = A UNION {(u, v)}
            // 合并这两个集合
            Union(u, v)
            
            // 优化：如果边数达到 V-1，可以提前退出循环
            IF size(A) == |V| - 1:
                BREAK

    RETURN A

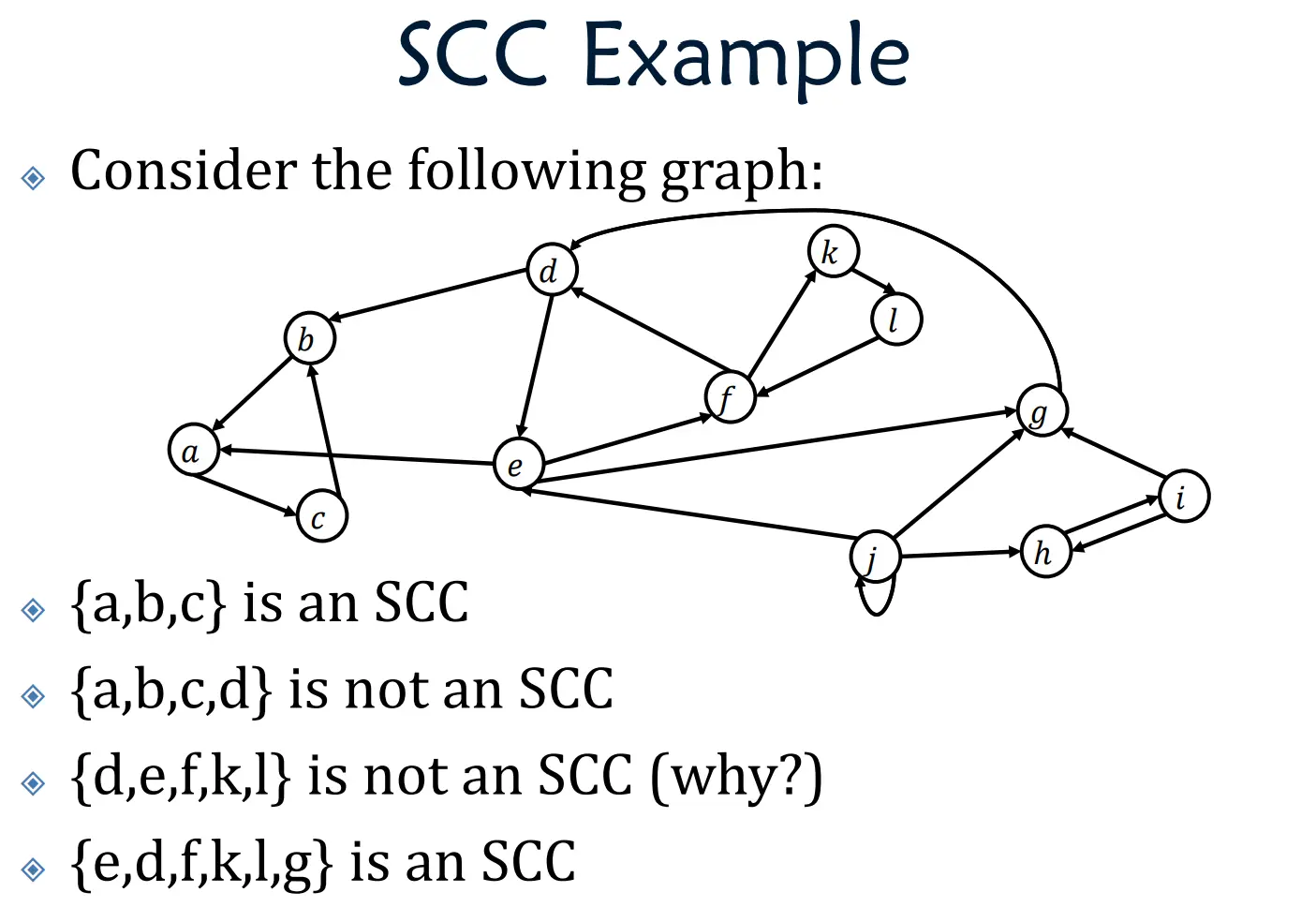
SCC 强连通分量

强连通分量 (Strongly Connected Component, 简称 SCC) 是有向图（Directed Graph）中一个非常重要的概念

• 强连通：如果从地点 A 能走到地点 B，且从地点 B 也能走回地点 A（即 A 和 B 互相可达），那么它们就是强连通的

• 强连通分量：就是把所有能互相到达的点圈在一起，形成的最大集合。在这个集合里，任何两个点都可以互相到达

1. 核心特征

1. 必须是有向图：无向图叫“连通分量”，有向图才叫“强连通分量”
2. 互相可达：集合内任意两个点 $u, v$，都存在 $u \to v$ 的路径，也存在 $v \to u$ 的路径
3. 极大性：你不能再往这个集合里添加任何一个新的点，否则就不满足“互相可达”的性质了

2. 求解 SCC（Kosaraju 算法）

Kosaraju 算法是用来求解有向图中 强连通分量 (SCC) 的一种算法，虽然它的效率比Tarjan 算法稍微慢一点点（因为它需要对图进行两次遍历，而 Tarjan 只需要一次），但是它的逻辑非常直观，容易理解和记忆

核心思想：两次 DFS

1. 第一次 DFS（正向图）：确定的“拓扑顺序”。我们要找出哪些点是“上游”的，哪些是“下游”的。我们把点按照“完成访问的时间”压入一个栈中
2. 反向图（Transpose Graph）：将原图中所有的边方向反转（$u \to v$ 变成 $v \to u$）
3. 第二次 DFS（反向图）：按照栈中弹出的顺序（从“上游”开始），在反向图中进行 DFS。每次能遍历到的所有点，就是一个强连通分量

伪代码：

Algorithm Kosaraju(Graph G, int N):
    // 初始化变量
    Stack stack
    Boolean[] visited = new Boolean[N] initialized to false
    List<List> sccList

    // -------------------------------------------------
    // 第一步：在原图上进行第一次 DFS
    // 目的：按照“完成时间”填充栈（拓扑排序的逆序）
    // -------------------------------------------------
    function DFS1(u):
        visited[u] = true
        for each v in G.adj[u]:
            if not visited[v]:
                DFS1(v)
        // 关键：在递归回溯时（离开节点前）将节点压入栈
        stack.push(u)

    // 对所有节点执行 DFS1，确保处理非连通图
    for i from 1 to N:
        if not visited[i]:
            DFS1(i)

    // -------------------------------------------------
    // 第二步：构建反向图
    // -------------------------------------------------
    Graph revG = createTransposeGraph(G)

    // -------------------------------------------------
    // 第三步：在反向图上进行第二次 DFS
    // 目的：按照栈的顺序剥离强连通分量 (SCC)
    // -------------------------------------------------
    // 重置访问标记
    visited = new Boolean[N] initialized to false

    function DFS2(u, currentSCC):
        visited[u] = true
        currentSCC.add(u)
        // 注意：这里遍历的是反向图的边
        for each v in revG.adj[u]:
            if not visited[v]:
                DFS2(v, currentSCC)

    // 不断从栈顶弹出节点
    while stack is not empty:
        u = stack.pop()
        if not visited[u]:
            // 发现一个新的强连通分量
            List component = new List()
            DFS2(u, component)
            sccList.add(component)

    return sccList

Java：

import java.util.*;
import java.io.*;

public class KosarajuAlgo {
    // 全局变量，方便在递归中使用
    static int n, m;
    static ArrayList<Integer>[] adj;     // 原图
    static ArrayList<Integer>[] revAdj;  // 反向图 (Reversed Graph)
    static boolean[] visited;            // 访问标记数组
    static Stack<Integer> stack;         // 存储第一次 DFS 的节点顺序
    
    // 存储结果：每个 List<Integer> 代表一个 SCC
    static List<List<Integer>> sccResults; 

    public static void main(String[] args) {
        // 模拟输入数据
        // 假设有 5 个点，5 条边
        // 1->2, 2->3, 3->1 (环), 3->4, 4->5
        n = 5;
        m = 5;
        
        // 1. 初始化图
        adj = new ArrayList[n + 1];
        revAdj = new ArrayList[n + 1];
        for (int i = 1; i <= n; i++) {
            adj[i] = new ArrayList<>();
            revAdj[i] = new ArrayList<>();
        }

        // 2. 添加边 (手动模拟输入)
        // 在实际题目中，这里放在循环里读取 u, v
        addEdge(1, 2);
        addEdge(2, 3);
        addEdge(3, 1);
        addEdge(3, 4);
        addEdge(4, 5);

        // 3. 执行 Kosaraju 算法
        solveKosaraju();

        // 4. 输出结果
        System.out.println("总共有 " + sccResults.size() + " 个强连通分量:");
        for (int i = 0; i < sccResults.size(); i++) {
            System.out.println("SCC #" + (i + 1) + ": " + sccResults.get(i));
        }
    }

    // 添加边的方法：同时构建原图和反向图
    // 注意：如果是题目输入，通常只给 u->v。
    // 我们在这里同时把 v加入revAdj[u]是不对的，应该是 u加入revAdj[v]
    static void addEdge(int u, int v) {
        adj[u].add(v);      // 原图: u -> v
        revAdj[v].add(u);   // 反向图: v -> u
    }

    static void solveKosaraju() {
        stack = new Stack<>();
        visited = new boolean[n + 1];

        // --- 步骤 1: 第一次 DFS (原图) ---
        for (int i = 1; i <= n; i++) {
            if (!visited[i]) {
                dfs1(i);
            }
        }

        // --- 步骤 2: 第二次 DFS (反向图) ---
        // 重置 visited 数组，因为我们要重新标记
        Arrays.fill(visited, false);
        sccResults = new ArrayList<>();

        // 按照栈的弹出顺序（拓扑逆序）进行处理
        while (!stack.isEmpty()) {
            int u = stack.pop();
            // 如果这个点在第二轮还没被访问过，说明它是新的 SCC 的起点
            if (!visited[u]) {
                List<Integer> currentSCC = new ArrayList<>();
                dfs2(u, currentSCC);
                sccResults.add(currentSCC);
            }
        }
    }

    // 第一次 DFS：目的是填充栈
    static void dfs1(int u) {
        visited[u] = true;
        for (int v : adj[u]) {
            if (!visited[v]) {
                dfs1(v);
            }
        }
        // 【关键】: 在递归结束、即将回溯时，将节点入栈
        // 这保证了栈顶元素是拓扑序中“最上游”的节点
        stack.push(u);
    }

    // 第二次 DFS：在反向图上运行，收集 SCC 节点
    static void dfs2(int u, List<Integer> currentSCC) {
        visited[u] = true;
        currentSCC.add(u); // 将当前点加入当前的 SCC 集合
        
        // 注意：这里遍历的是 revAdj (反向图)
        for (int v : revAdj[u]) {
            if (!visited[v]) {
                dfs2(v, currentSCC);
            }
        }
    }
}

杂鱼 ❤~

主定理

$$T(n) = aT(n/b) + cn^d$$

想象你在处理一个大任务（比如整理 1000 份文件）：

• $n$: 文件的总数（问题规模）
• $a$: 你把任务分给了 $a$ 个下属（子问题数量）
• $b$: 每个下属分到的任务量是原来的 $1/b$（子问题规模缩小倍数）
• $cn^d$: 你作为老板，把任务分发下去以及最后汇总结果所花的时间（分治的开销）

三种情况

我们需要比较 $a$ 和 $b^d$ 的大小

情况 1：子问题太多了 (叶子赢了)

• 条件： $a > b^d$

• 含义： 任务分裂得太快，虽然单个子问题变小了，但架不住数量多。大部分时间都花在了递归树的最底层（即处理成千上万个极小的子问题）

• 结果： 复杂度由叶子数量决定

$$T(n) = \Theta(n^{\log_b a})$$

(注意：$\log_b a$ 其实就是递归树底部的叶子节点数量指数)

情况 2：完美平衡

• 条件： $a = b^d$

• 含义： 子问题分裂的速度，正好被规模缩小的速度抵消了。递归树的每一层，总的工作量都是一样的。

• 结果： 总时间 = (每一层的工作量) $\times$ (树的高度)

  • 每一层工作量是 $n^d$

  • 树的高度是 $\log_b n$

$$T(n) = \Theta(n^d \log n)$$

情况 3：合并代价太大

• 条件： $a < b^d$

• 含义： 相比于子问题的增长，你在每一层做“分解和合并”的代价太大了（通常是因为 $d$ 很大）。大部分时间都花在了递归树的顶层（根节点）。随着递归深入，工作量迅速衰减

• 结果： 复杂度由顶层（根节点）的工作量决定

$$T(n) = \Theta(n^d)$$

例子 1：归并排序 (Merge Sort)

公式：$T(n) = 2T(n/2) + n$

• 参数： $a=2$ (分成两份), $b=2$ (每份一半), $cn^1$ (合并耗时 $O(n)$，所以 $d=1$)。
• 比较：
  • $a = 2$
  • $b^d = 2^1 = 2$
  • 结论： $2 = 2$，属于 情况 2 (平衡型)。
• 答案： $T(n) = \Theta(n^1 \log n) = \Theta(n \log n)$

例子 2：二分查找 (Binary Search)

公式：$T(n) = 1T(n/2) + c$

• 参数： $a=1$ (只查一边), $b=2$ (规模减半), $c = c \cdot n^0$ (常数项，所以 $d=0$)。
• 比较：
  • $a = 1$
  • $b^d = 2^0 = 1$
  • 结论： $1 = 1$，属于 情况 2 (平衡型)。
• 答案： $T(n) = \Theta(n^0 \log n) = \Theta(\log n)$

Rabin-Karp && 滚动哈希

Rabin-Karp 的精髓在于如何在 $O(1)$ 的时间内算出下一个窗口的哈希值

示例：

设定环境

1. 字符映射 (Mapping)：

   我们将 4 个字符映射为 4 个整数：

   • A = 1
   • C = 2
   • G = 3
   • T = 4

2. 进制 (Base)：4

   （因为只有 4 种字符，类似二进制、十六进制，这里我们用四进制）。

3. 模数 (Modulus $Q$)：11

   （为了演示方便，选一个很小的质数，方便心算验证）。

4. 任务：

   • 文本 (Text): C A T G C
   • 模式 (Pattern): A T G
   • 窗口长度 ($m$): 3

第一步：准备工作

在开始滚动之前，我们需要算一个常数 $h$，它是最高位字符的权重。

公式：$h = \text{Base}^{m-1} \pmod Q$

• $Base = 4$
• $m - 1 = 2$
• $Q = 11$

计算：

$$h = 4^2 \pmod{11} = 16 \pmod{11} = \mathbf{5}$$

(记住这个 5，后面每次移除旧字符时都要用到它)

第二步：计算目标（模式串）的哈希

我们要找的是 A T G，对应数值：1, 4, 3
我们要把它看作一个四进制数 $(143)_4$：

$$1 \cdot 4^2 + 4 \cdot 4^1 + 3 \cdot 4^0$$

计算过程：

1. $1 \cdot 16 = 16$
2. $4 \cdot 4 = 16$
3. $3 \cdot 1 = 3$
4. 和 $= 16 + 16 + 3 = 35$

取模：

$$H_{target} = 35 \pmod{11} = \mathbf{2}$$

我们的目标就是找到哈希值为 2 的窗口。

第三步：初始化第一个窗口

文本的开头是 C A T，对应数值：2, 1, 4

计算这个四进制数 $(214)_4$ 的值：

$$2 \cdot 4^2 + 1 \cdot 4^1 + 4 \cdot 4^0$$

$= 32 + 4 + 4 = 40$

取模：

$$H_{curr} = 40 \pmod{11} = \mathbf{7}$$

比较：

当前哈希是 7，目标是 2。

$7 \neq 2$，不匹配。我们需要向右滑动。

第四步：滚动哈希 (关键步骤)

我们将窗口从 [C A T] 滑动到 [A T G]。

• 旧哈希 ($H_{old}$): 7
• 移出字符: C (对应数值 2)
• 移入字符: G (对应数值 3)
• 进制 ($Base$): 4
• 高位权重 ($h$): 5
• 模数 ($Q$): 11

公式回顾：

$$H_{new} = \left( (H_{old} - \text{移出} \cdot h) \cdot Base + \text{移入} \right) \pmod Q$$

详细计算步骤：

1. 移除最高位 (Remove High):

   $$H_{old} - (\text{数值}_C \cdot h)$$

   $$= 7 - (2 \cdot 5)$$

   $$= 7 - 10 = \mathbf{-3}$$

   关键点：出现负数了！

   在计算机取模运算中，负数处理要很小心。我们通常加上一个模数 $Q$ 让它变正。

   $-3 \pmod{11}$ 等同于 $(-3 + 11) \pmod{11} = \mathbf{8}$

   (现在结果是 8)

2. 左移一位 (Shift):

   相当于乘以进制 Base。

   $$8 \cdot 4 = 32$$

   为了防止数字过大，这里可以随时取模（也可以最后取，结果一样）。

   $$32 \pmod{11} = \mathbf{10}$$

   (现在结果是 10，这代表了 ‘AT’ 部分的哈希)

3. 加入最低位 (Add Low):

   加上新进来的字符 G (数值 3)

   $$10 + 3 = 13$$

4. 最终取模:

   $$13 \pmod{11} = \mathbf{2}$$

结果： 新窗口 A T G 的哈希值是 2

第五步：验证

• 当前窗口哈希：2
• 目标模式哈希：2
• 匹配成功！ (Hash Hit)

最后一步是二次确认（防止哈希冲突）：
程序会去对比字符串 A T G 和模式串 A T G 是否真的相等。