机器学习笔记

课程主页
配套练习代码

1. 监督学习

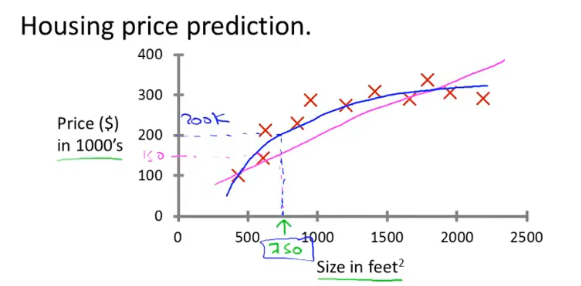
监督学习是已经知道数据的label，例如预测房价问题，给出了房子的面积和价格

• 回归问题是预测连续值的输出，例如预测房价

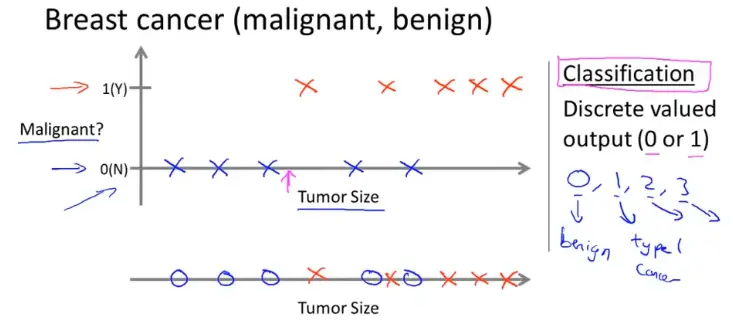
• 分类问题是预测离散值输出，例如判断肿瘤是良性还是恶性

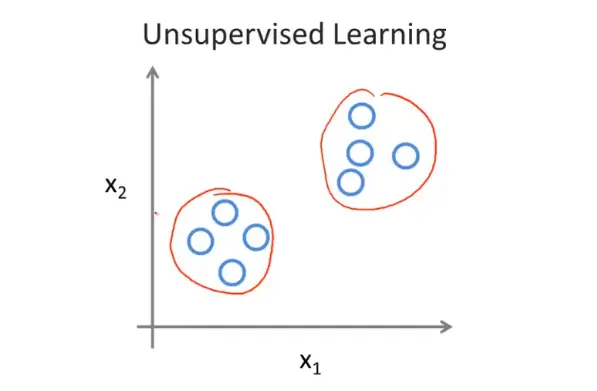
2. 无监督学习

无监督学习是不知道数据具体的含义，比如给定一些数据但不知道它们具体的信息，对于分类问题无监督学习可以得到多个不同的聚类，从而实现预测的功能

3. 线性回归

3.1 代价函数（Cost Function)

最小二乘法

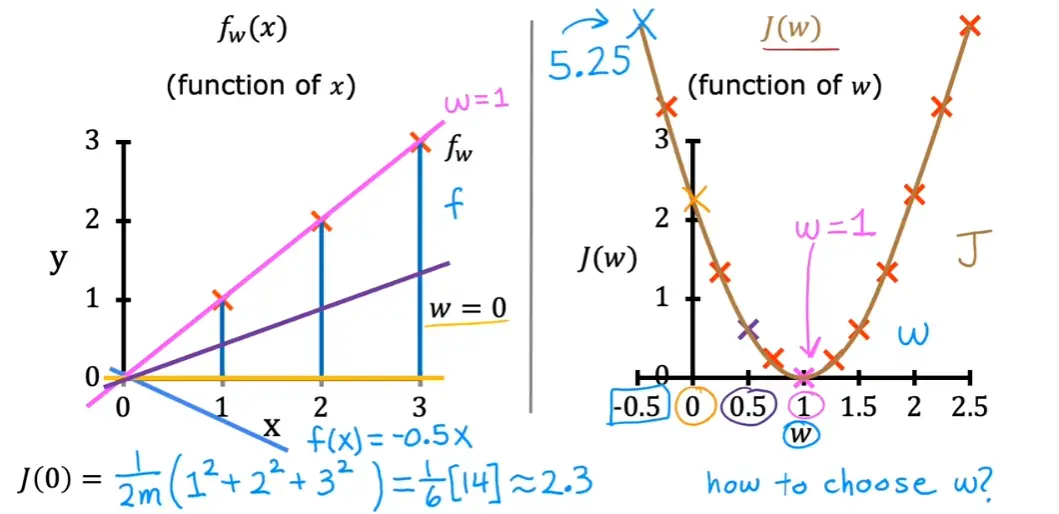
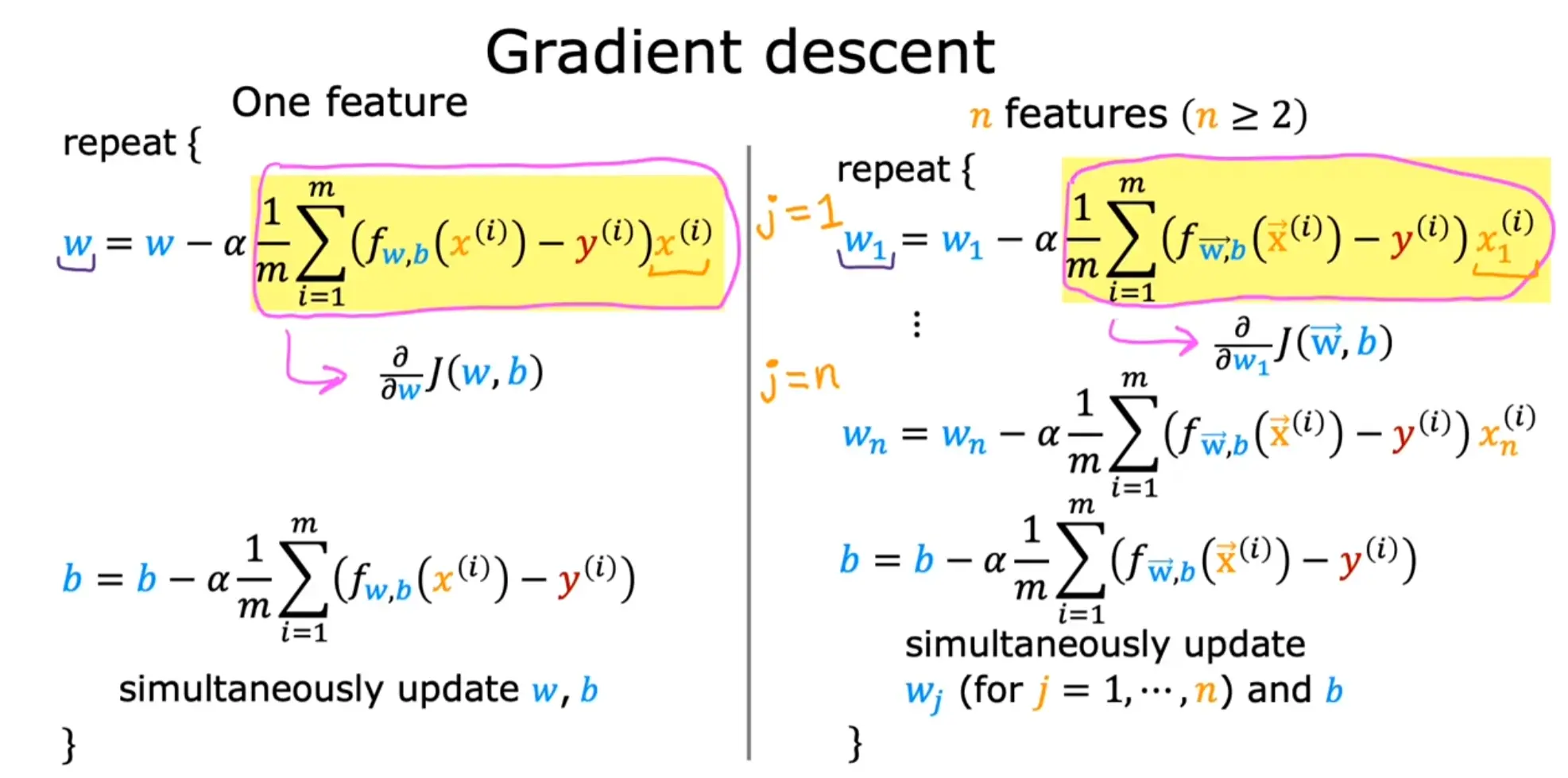
3.2 梯度下降（Gradient Descent）

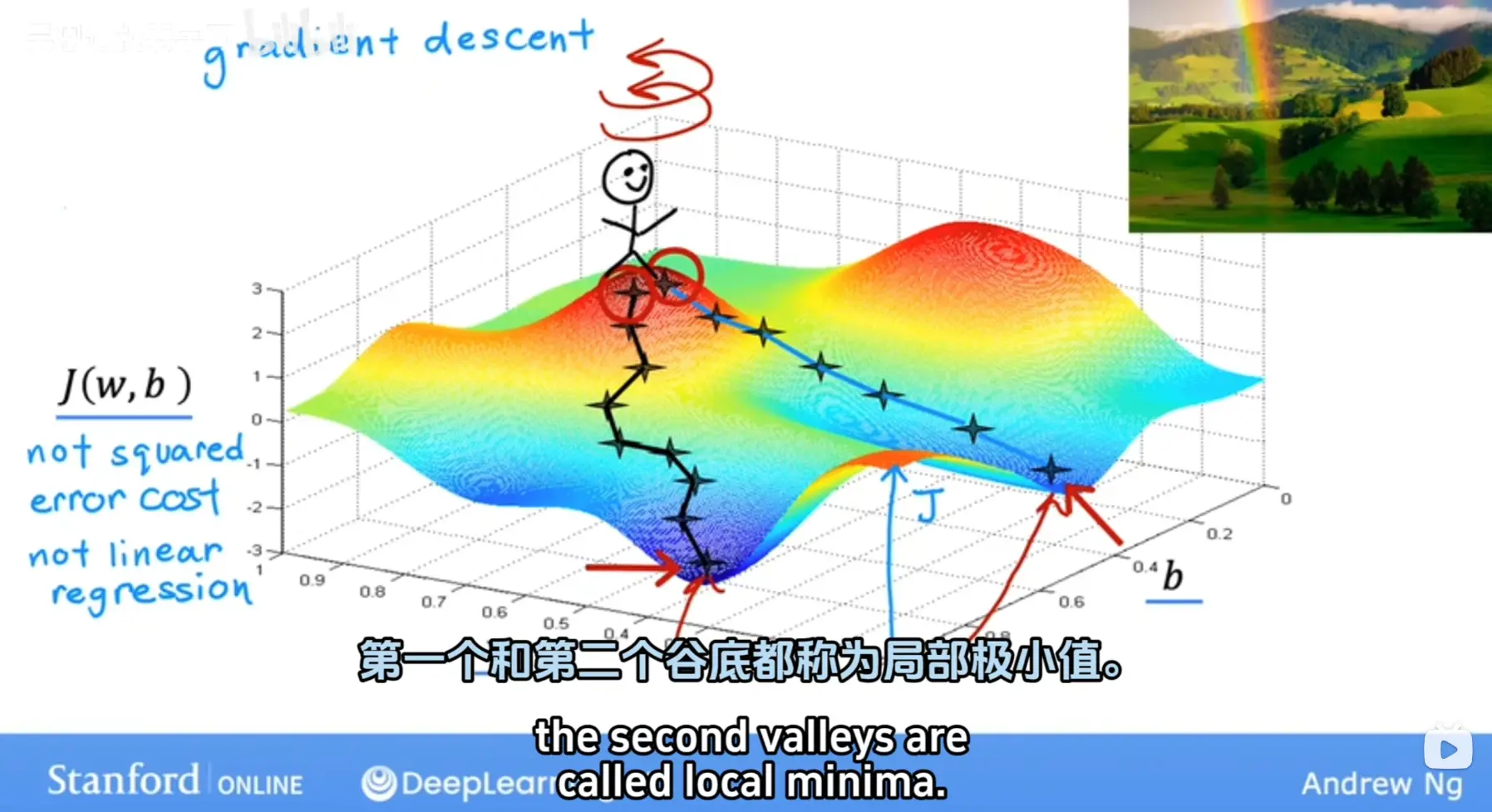
梯度下降，首先为每个参数赋一个初值，通过代价函数的梯度，然后不断地调整参数，最终得到一个局部最优解。初值的不同可能会得到两个不同的结果，即梯度下降不一定得到全局最优解

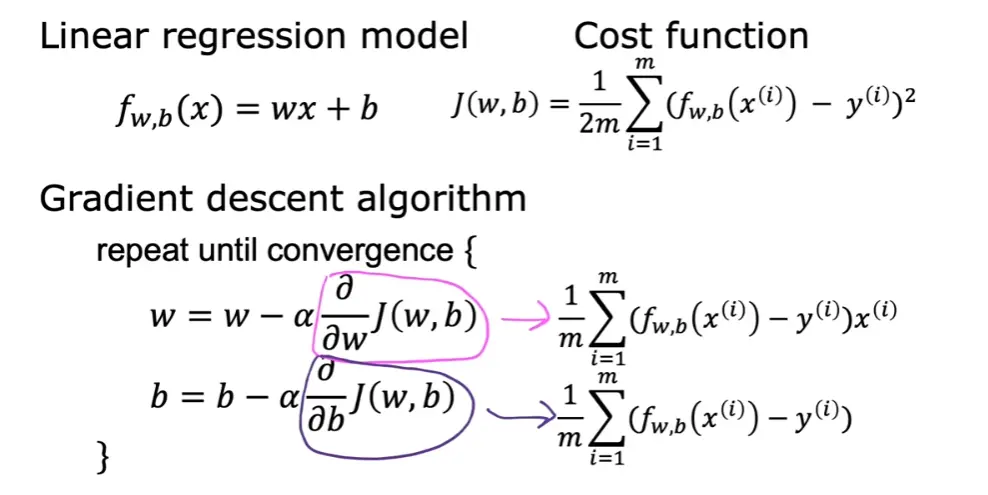
梯度下降在具体的执行时，每一次更新需要同时更新所有的参数。

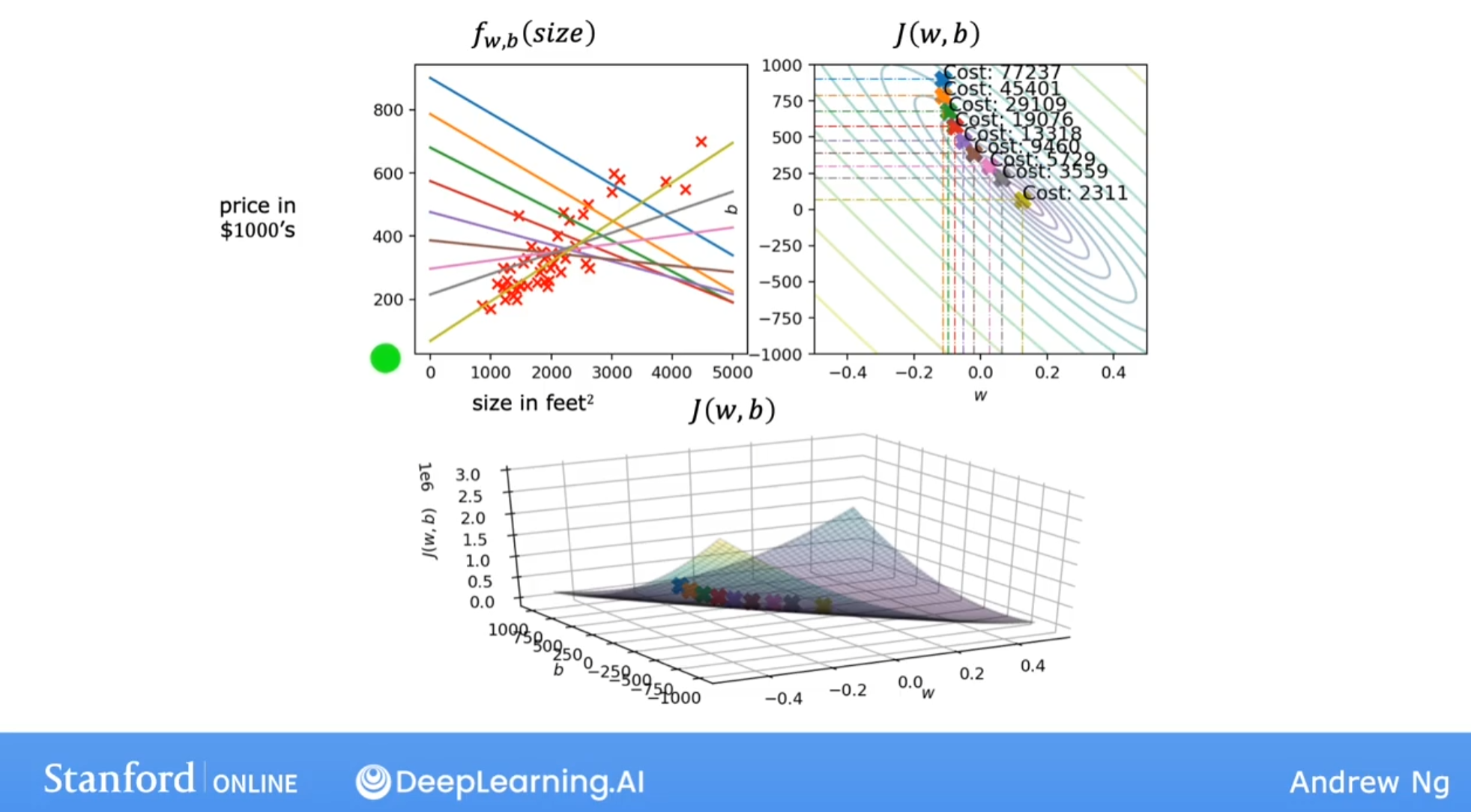
梯度下降效果图示

梯度下降过程容易出现局部最优解

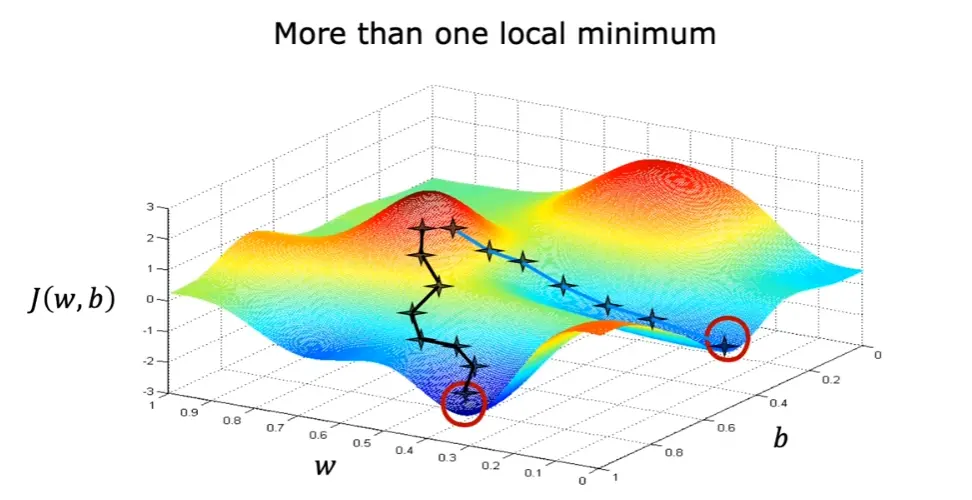
但是线性回归的代价函数往往是凸函数，总能收敛到全局最优解

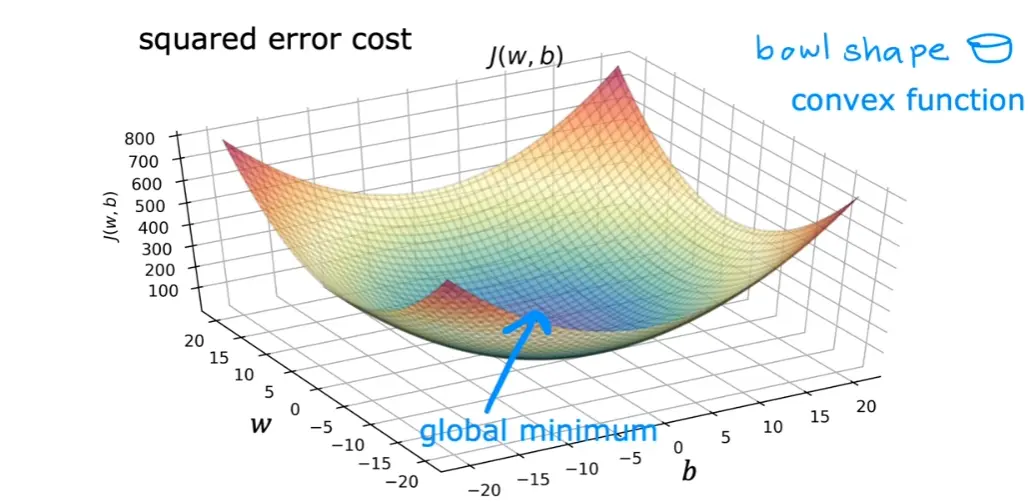
学习曲线：

学习率: 过小下降慢，过大可能无法收敛

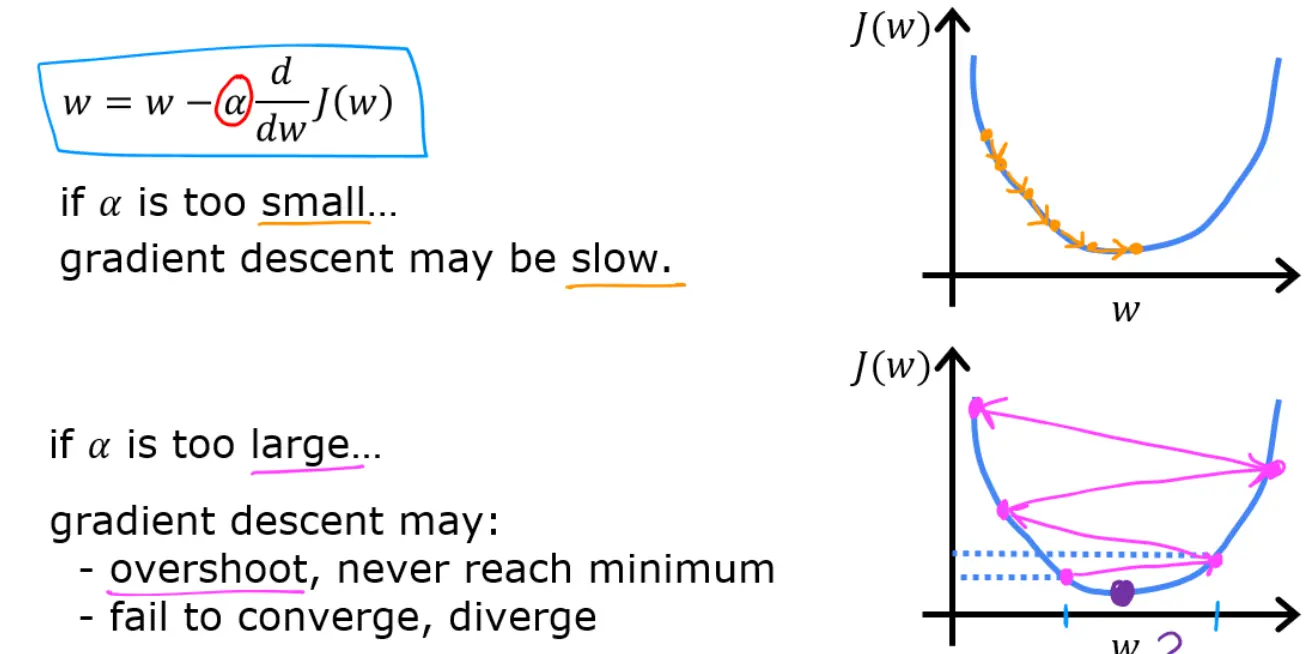
寻找最佳学习率

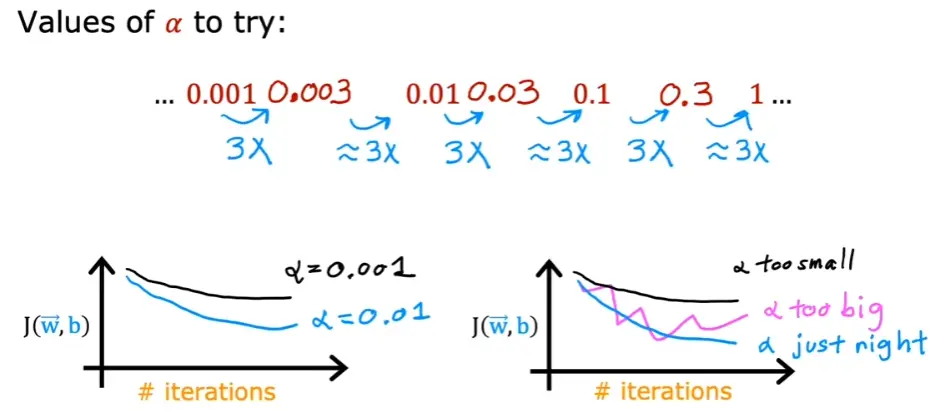
多元梯度下降与向量化

通常问题都会涉及到多个变量，例如房屋价格预测就包括，面积、房间个数、楼层、价格等

而向量化进行矩阵运算可以显著提高运算效率

$$\mathbf{X} = \begin{pmatrix} x^{(0)}_0 & x^{(0)}_1 & \cdots & x^{(0)}_{n-1} \\ x^{(1)}_0 & x^{(1)}_1 & \cdots & x^{(1)}_{n-1} \\ \cdots \\ x^{(m-1)}_0 & x^{(m-1)}_1 & \cdots & x^{(m-1)}_{n-1} \end{pmatrix}$$

Notation:

• $\mathbf{x}^{(i)}$ is vector containing example i. $\mathbf{x}^{(i)}$ $ = (x^{(i)}_0, x^{(i)}1, \cdots,x^{(i)}{n-1})$
• $x^{(i)}_j$ is element j in example i. The superscript in parenthesis indicates the example number while the subscript represents an element.

$$\mathbf{w} = \begin{pmatrix} w_0 \\ w_1 \\ \cdots\\ w_{n-1} \end{pmatrix}$$

$$f_{\mathbf{w},b}(\mathbf{x}) = w_0x_0 + w_1x_1 +... + w_{n-1}x_{n-1} + b = \mathbf{w} \cdot \mathbf{x} + b$$

3.3 正规方程（Normal Equation）

正规方程是一种解析解方法，可直接求解线性回归的最优参数，无需迭代优化。

假设线性回归模型为：

$$y = XW + \varepsilon$$

其中：

• $X$ 是特征矩阵（包含偏置项 $x_0 = 1$）。
• $W$ 是待求参数向量。
• $y$ 是目标值向量。
• $\varepsilon$ 是误差项。

最优参数 $W$ 由正规方程计算：

$$W = (X^T X)^{-1} X^T y$$

其中：

• $X^T X$ 是一个 正规矩阵（为了求逆转为方阵，正规矩阵可以用酉矩阵对角化）
• $(X^T X)^{-1}$ 是它的逆矩阵（如果可逆）
• $X^T y$ 是特征与目标值的内积

正规方程求解方法与梯度下降对比：

正规方程只能求解线性回归，且计算 $(X^T X)^{-1}$ 需要 $O(n^3)$ 复杂度，计算成本高

3.4 特征缩放

多个变量的度量不同，数字之间相差的大小也不同，如果可以将所有的特征变量缩放到大致相同范围，这样会减少梯度算法的迭代

特征缩放不一定非要落到[-1，1]之间，只要数据足够接近就可以

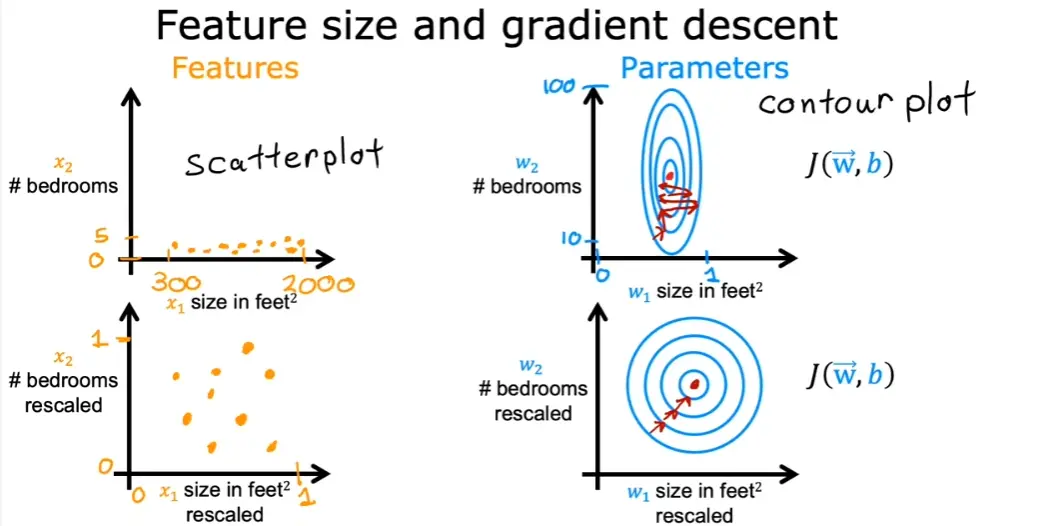
法一：均值归一化

法二：Z-score 标准化

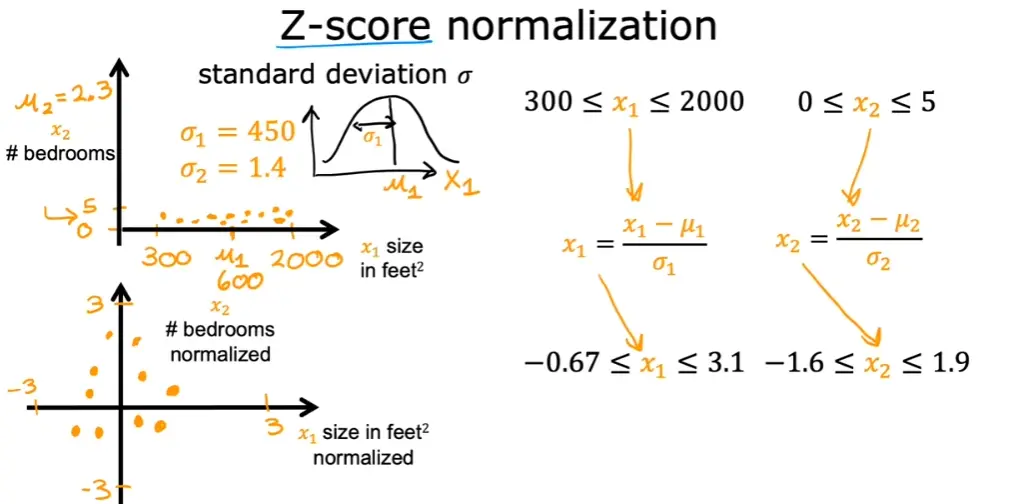
3.5 特征工程

通过转换和组合原始特征，形成新的特征，能使学习算法做出更准确的预测

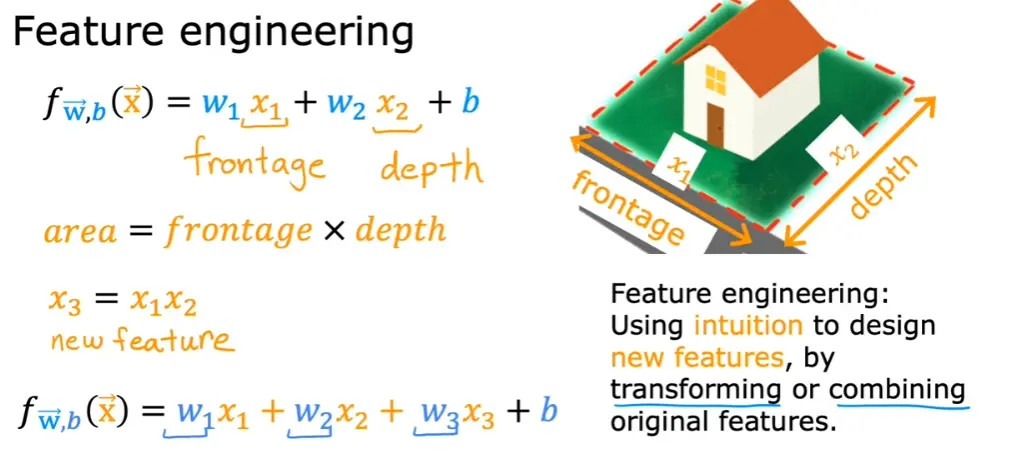
3.6 多项式回归

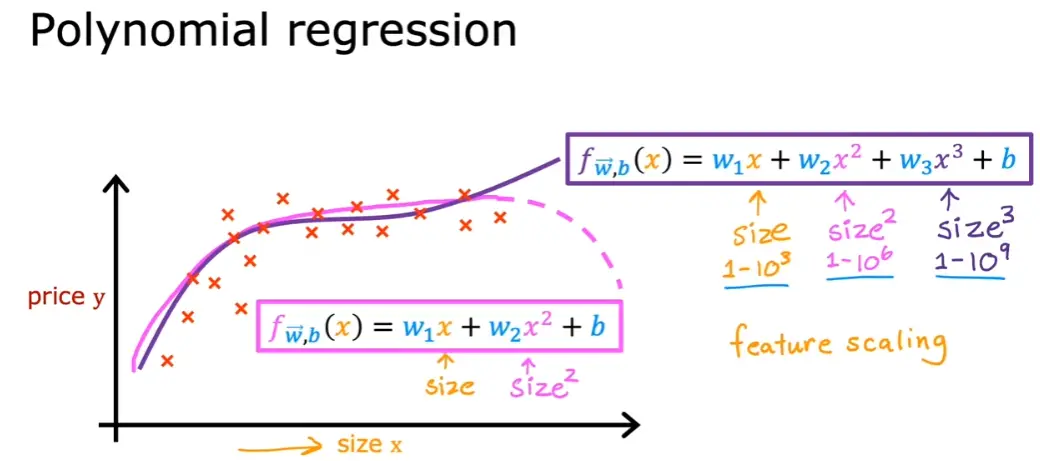
4. 逻辑回归

4.1 激活函数（Sigmoid Function）

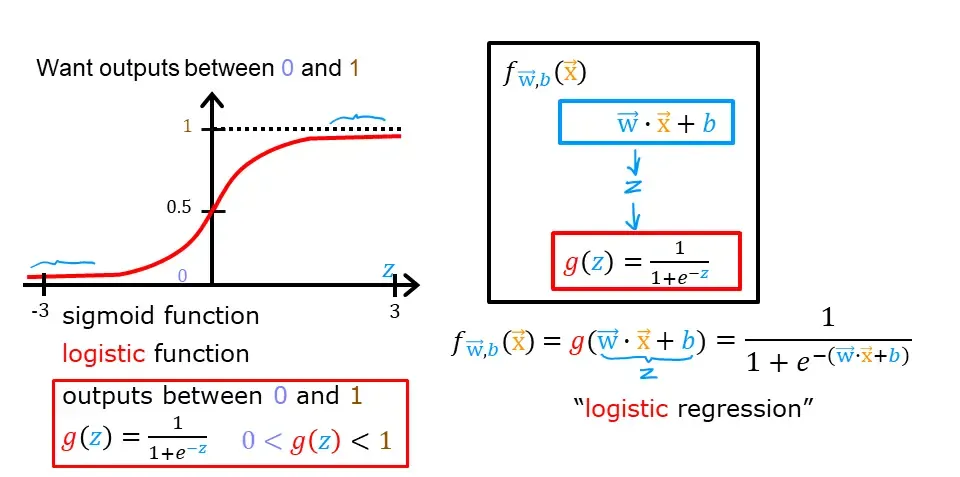
4.2 决策边界

$\begin{array}{rrr}\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b \geq 0 & \hat{y}=1 & \\ \overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b<0 & \hat{y}=0\end{array}$

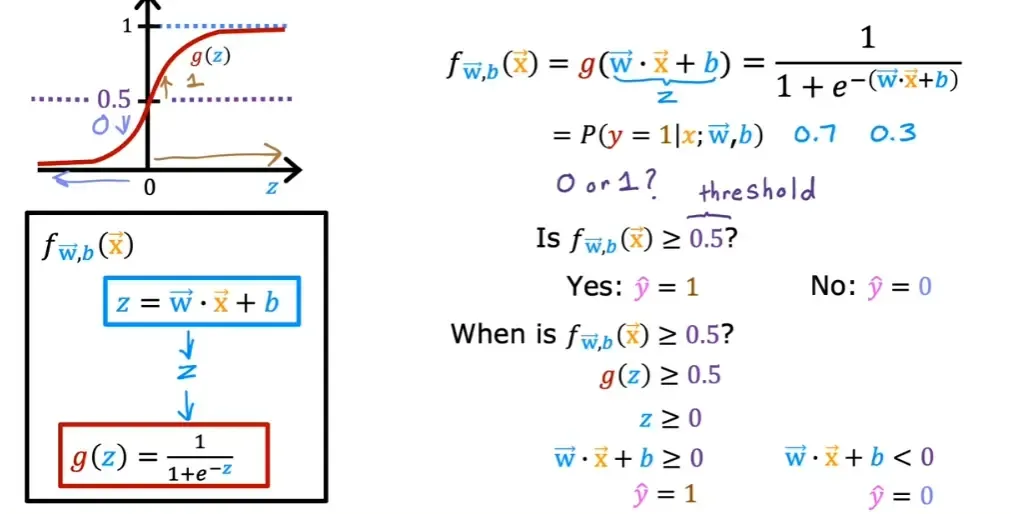
非线性的决策边界同理

4.3 代价函数

对于Sigmoid函数，如果使用线性回归中的代价函数$J(w, b)=\frac{1}{2 m} \sum_{i=0}^{m-1}\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right)^2$，将会得到一个非凸函数，使得无法使用梯度下降收敛到全局最优解

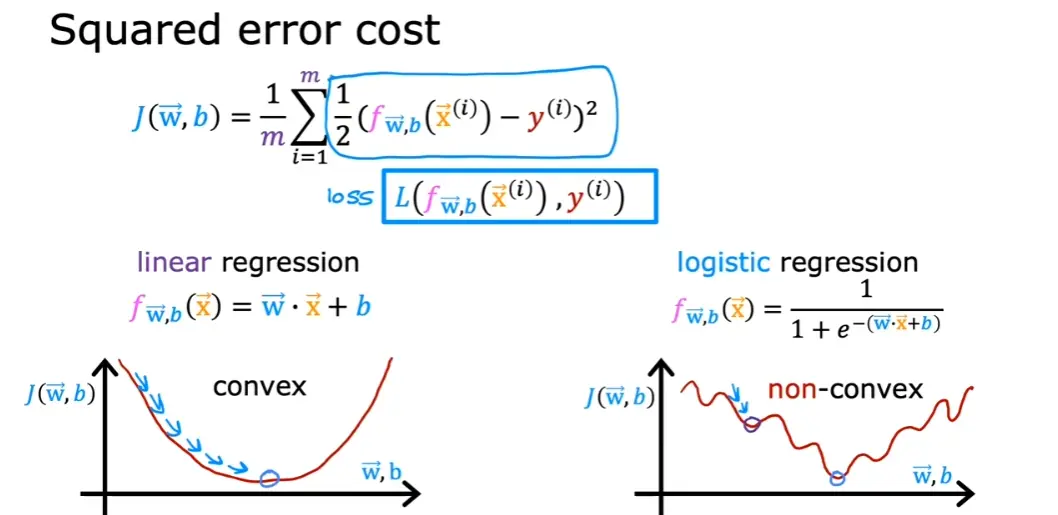
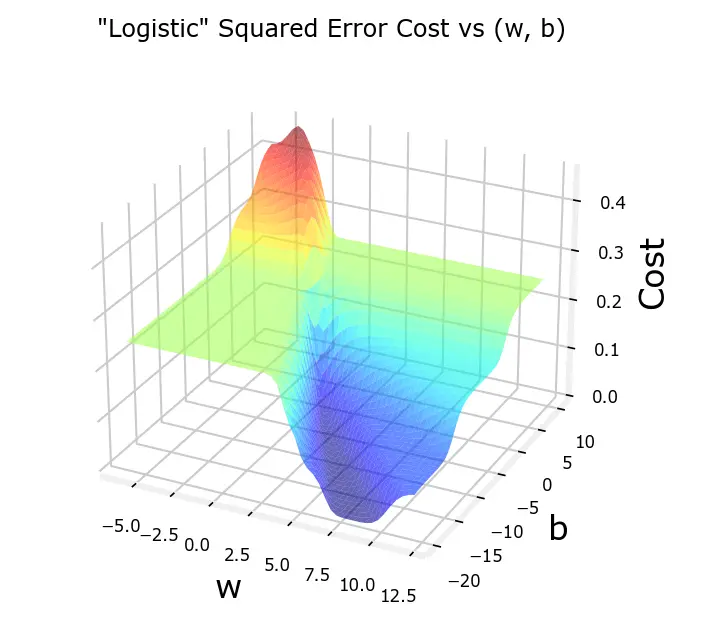
逻辑回归中一般使用对数函数作为损失函数

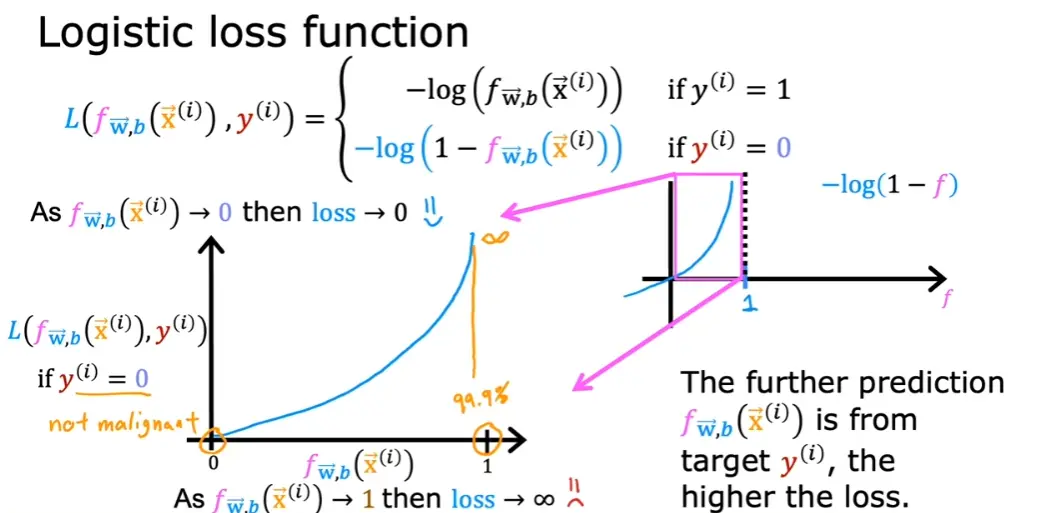
效果如图

$$loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = \begin{cases} - \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) & \text{if $y^{(i)}=1$}\\ - \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) & \text{if $y^{(i)}=0$} \end{cases}$$

可以将其合并为一条式子

$$loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = (-y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right)$$

将其代入代价函数得到

$$\begin{aligned} & J(\overrightarrow{\mathrm{w}}, b)=\frac{1}{m} \sum_{i=1}^m{L\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right), y^{(i)}\right)} \\ &=-\frac{1}{m} \sum_{i=1}^m\left[y^{(i)} \log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)\right] \end{aligned}$$

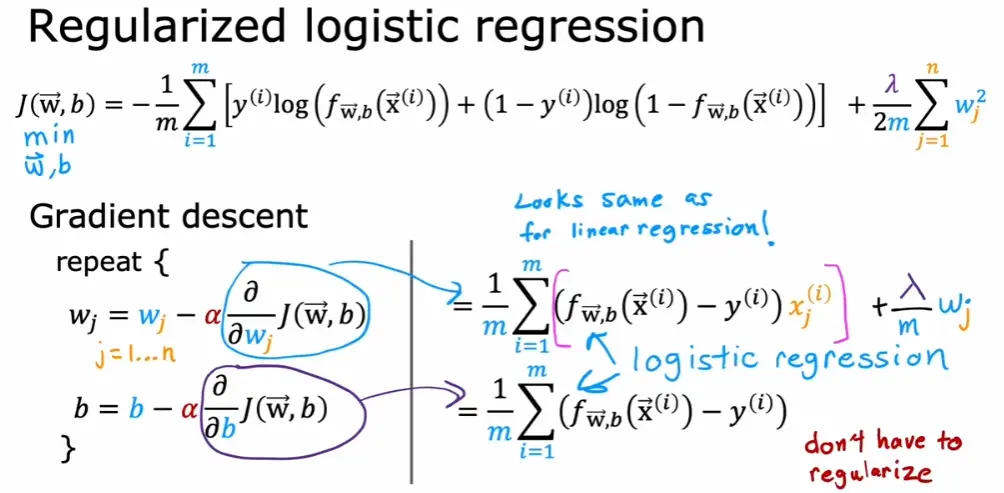
4.4 梯度下降

与线性回归中的梯度下降同理

推导过程参考

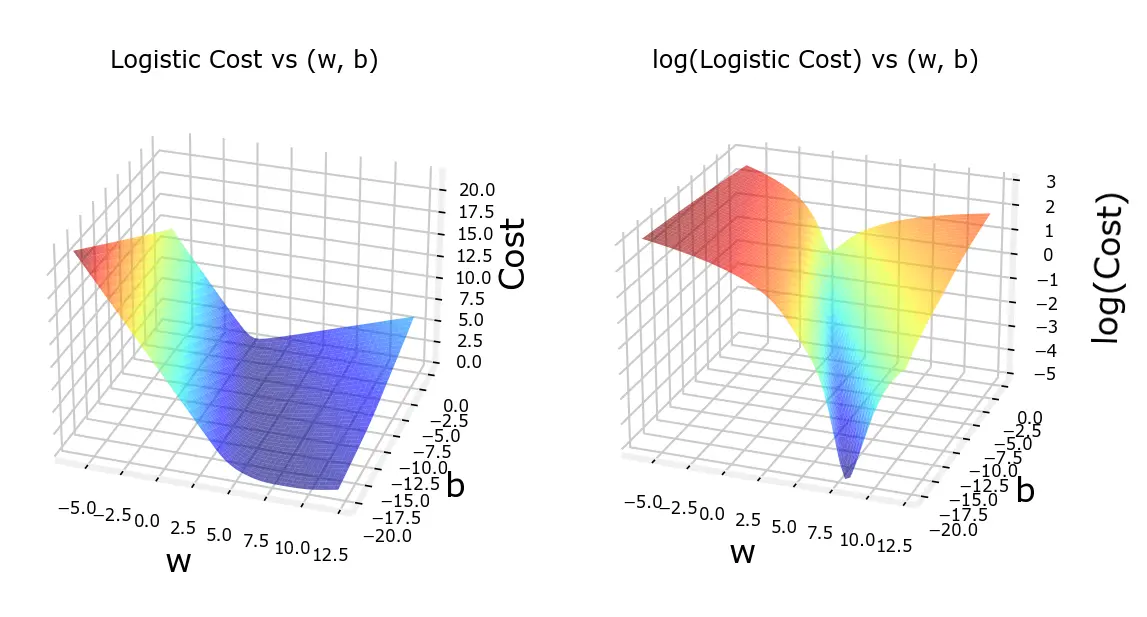
效果如图

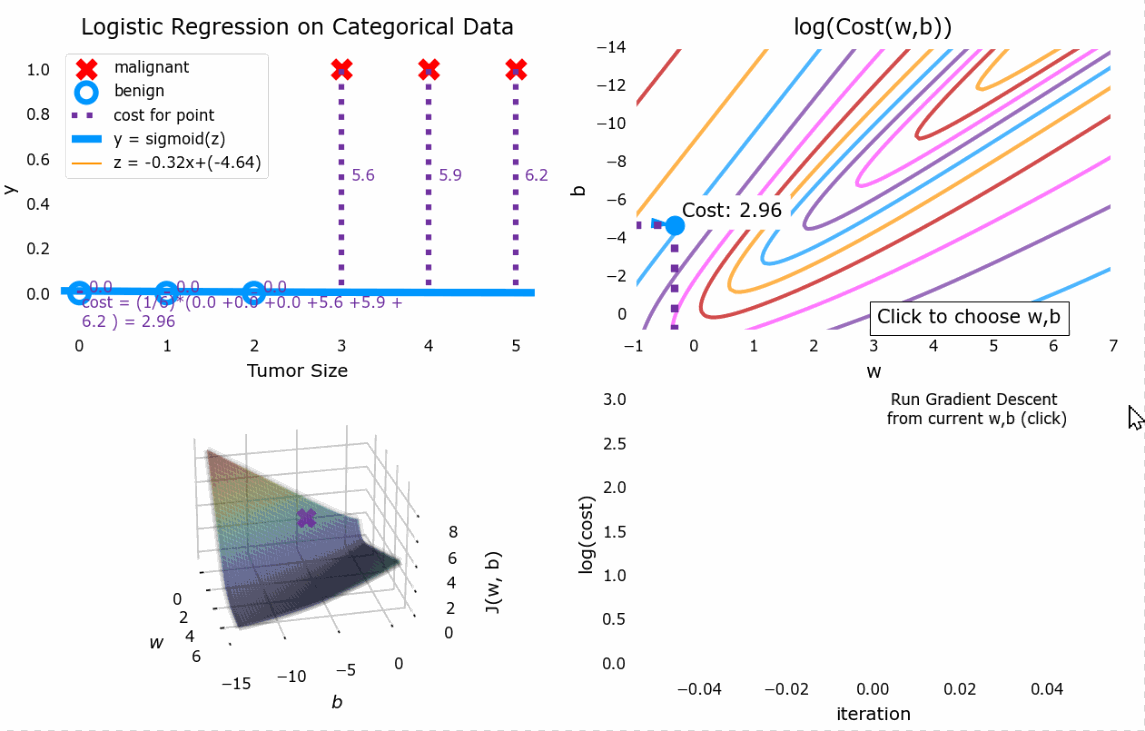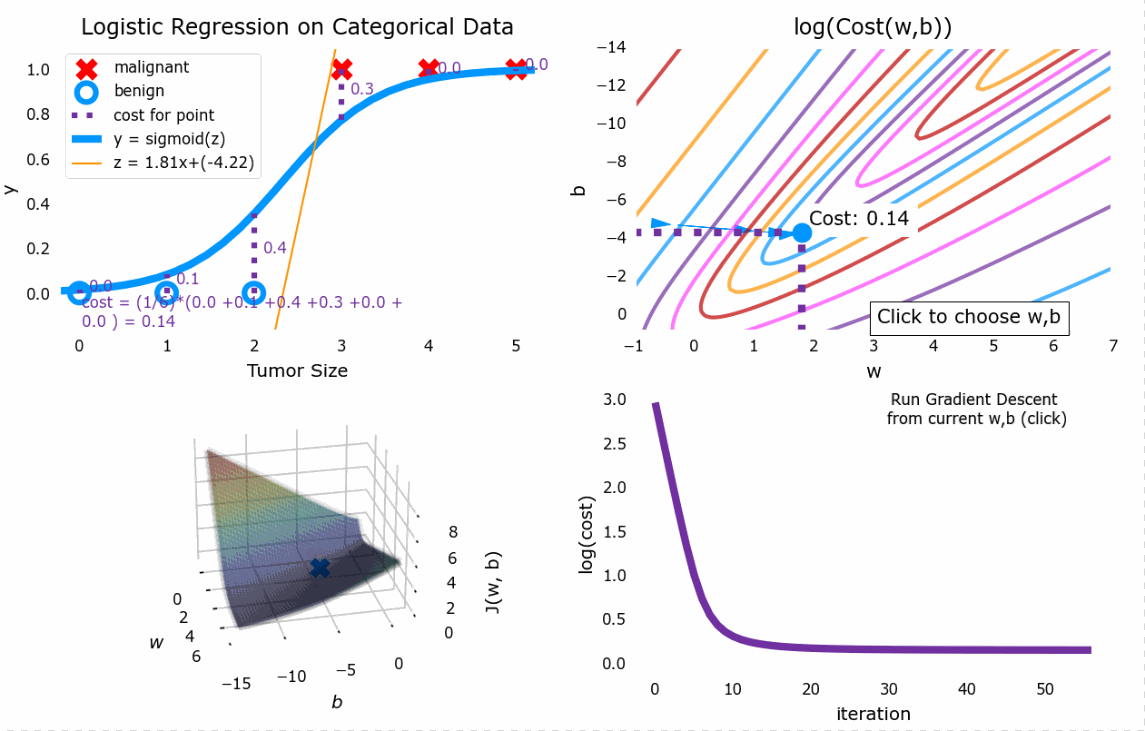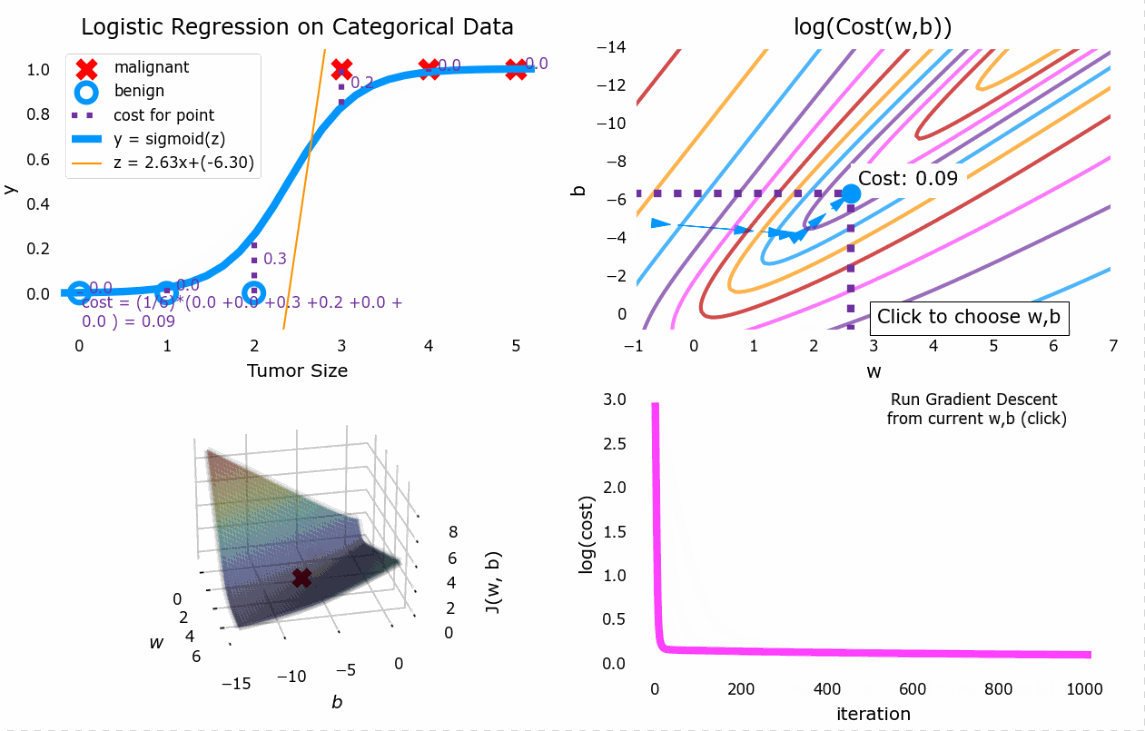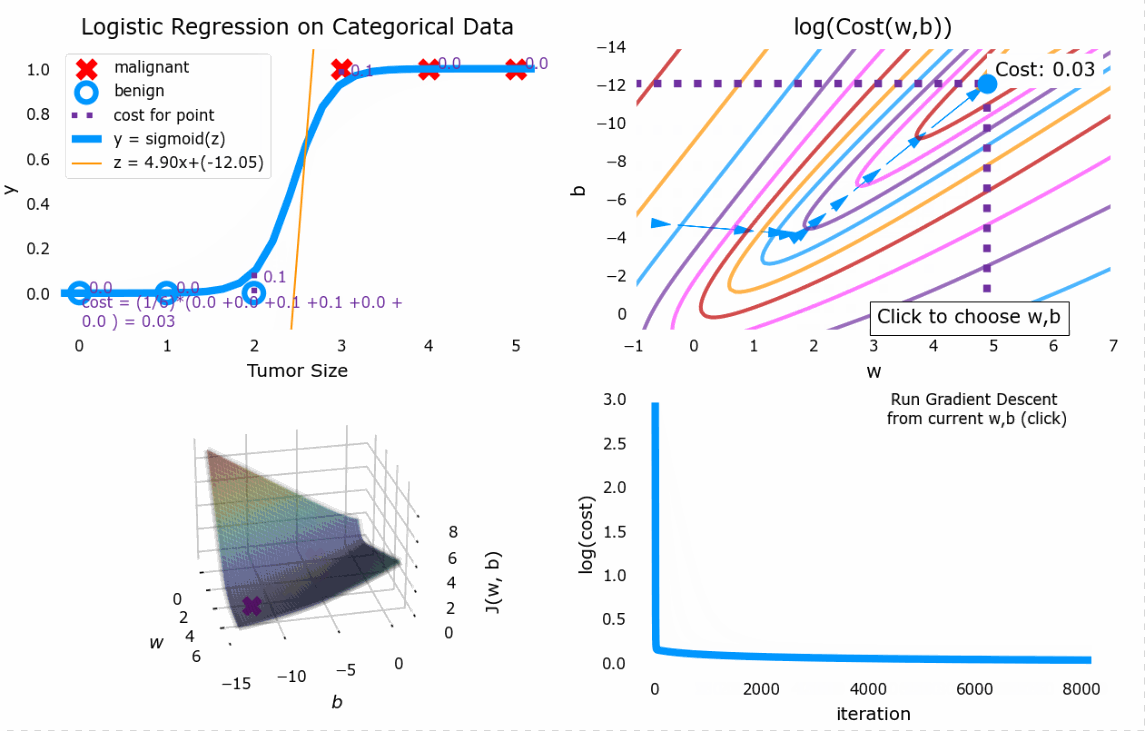
5. 过拟合与正则化

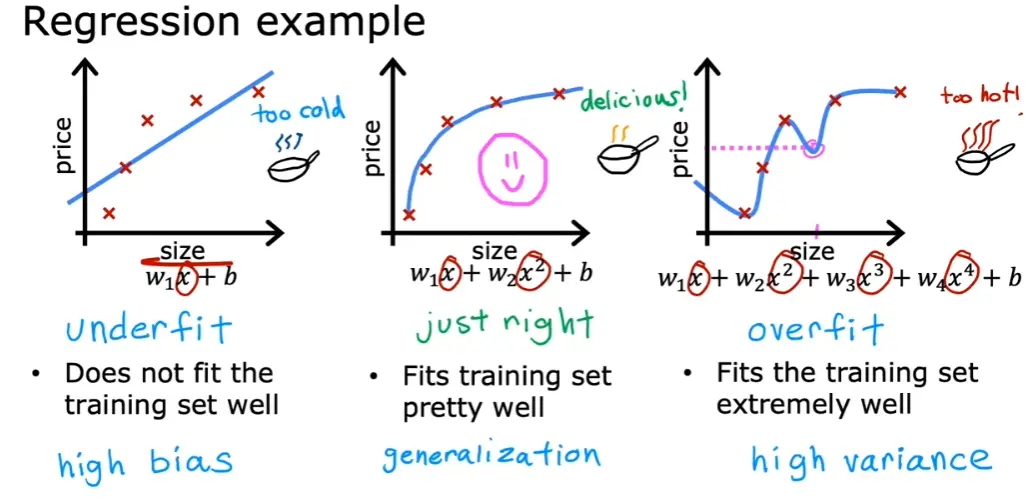
5.1 过拟合与欠拟合

• 过拟合 - 高偏差（high bias）
• 欠拟合 - 高方差（high variance）

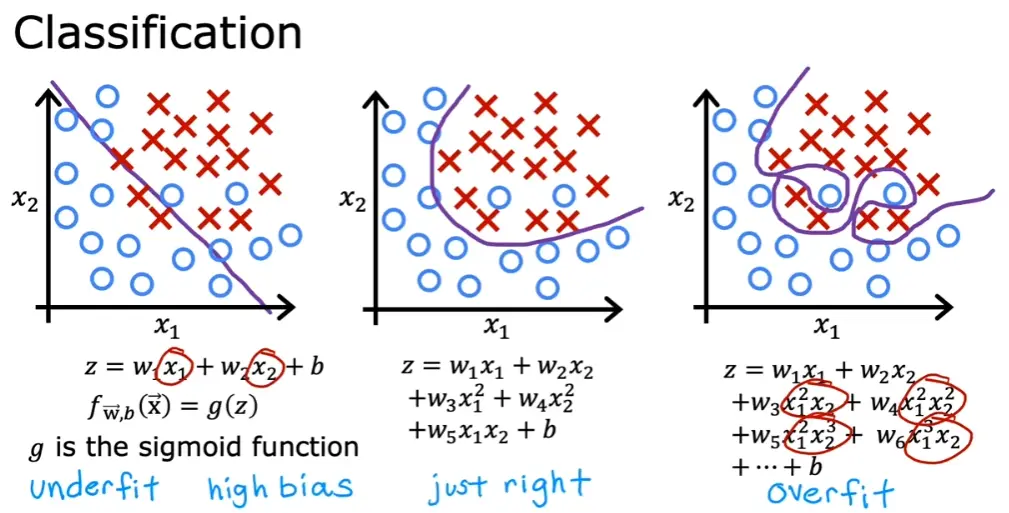
5.2 缓解过拟合的方法

1. 增加训练数据

   

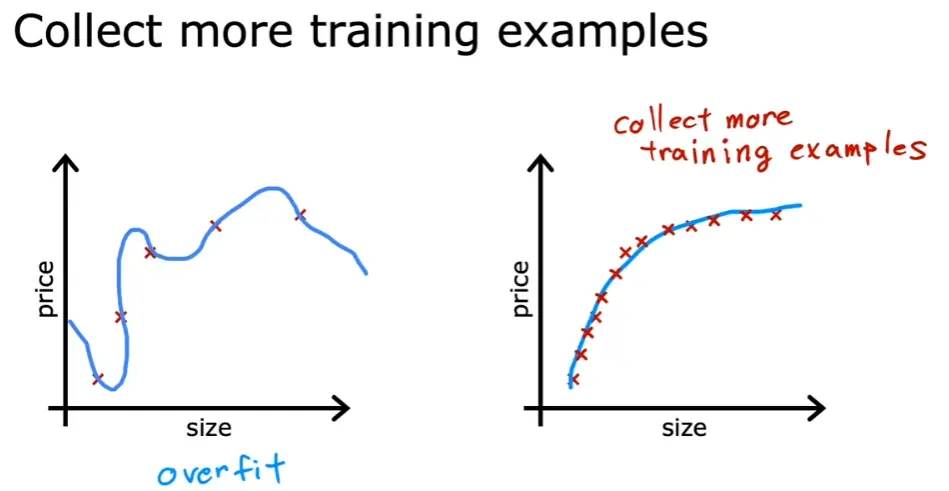
2. 减少特征数量，选取关键特征

   

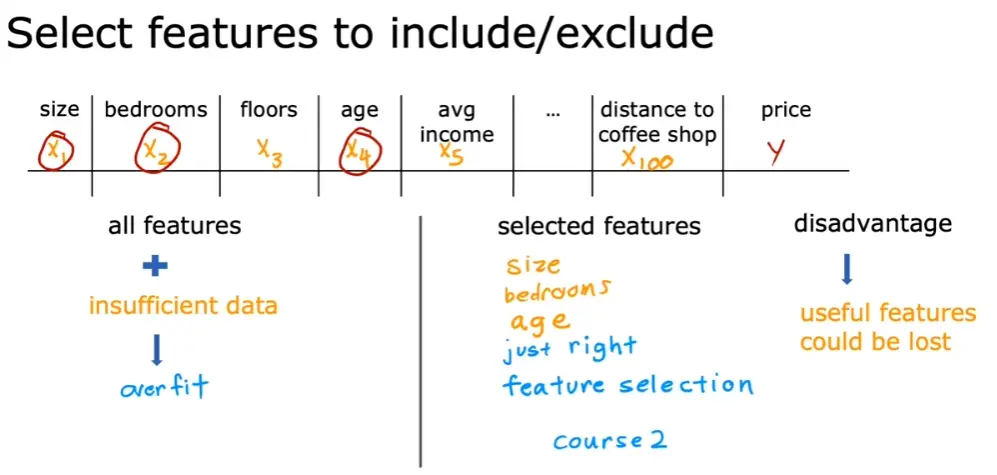
3. 正则化

   通过在代价函数末尾加多几项来惩罚对应的 $\omega$，从而减小其值，使曲线更加平滑

   

   

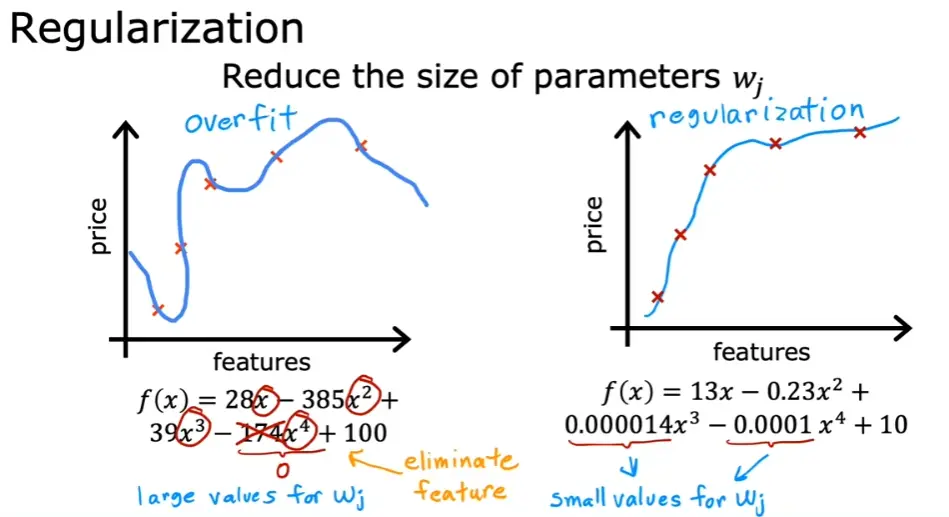
5.3 线性回归中的正则化

5.4 逻辑回归中的正则化