灰色预测 GM(1,1)
灰色系统理论旨在解决小样本 、贫信息 下的不确定性问题。它不追求数据的统计规律,而是通过特定方法处理原始数据,寻找其内在的发展趋势
GM(1,1)是该理论中最基础的模型,其名称含义为:G rey M odel of First-order equation in One variable(一阶单变量灰色模型)
其核心操作是累加生成(AGO) ,即将原始的、可能看似杂乱的数据序列进行累加,生成一个更平滑、趋势性更强的序列,然后对这个新序列建模
为了直观理解,可以将数据预测过程比作观察并预测一棵树的生长:
原始数据 X ( 0 ) X^{(0)} X ( 0 ) : 你每天 测量的树的生长量(例如:2cm, 3cm, 2.5cm…)。数据波动较大累加数据 X ( 1 ) X^{(1)} X ( 1 ) : 树的累计总高度 (例如:2cm, 5cm, 7.5cm…)。这条曲线比每日生长量平滑得多GM(1,1)的目标 : 通过对相对规律的“总高度”曲线进行建模,来反向推断并预测未来不规律的“每日生长量”
核心步骤
假设原始非负数据序列为 X ( 0 ) = ( x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) ) X^{(0)} = (x^{(0)}(1), x^{(0)}(2), \dots, x^{(0)}(n)) X ( 0 ) = ( x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ))
1. 累加生成 (AGO)
目的 :削弱原始数据的随机性,使其呈现单调趋势X ( 0 ) X^{(0)} X ( 0 ) X ( 1 ) X^{(1)} X ( 1 )
x ( 1 ) ( k ) = ∑ i = 1 k x ( 0 ) ( i ) x^{(1)}(k) = \sum_{i=1}^{k} x^{(0)}(i)
x ( 1 ) ( k ) = i = 1 ∑ k x ( 0 ) ( i )
x ( 1 ) ( 1 ) = x ( 0 ) ( 1 ) x^{(1)}(1) = x^{(0)}(1) x ( 1 ) ( 1 ) = x ( 0 ) ( 1 ) x ( 1 ) ( 2 ) = x ( 0 ) ( 1 ) + x ( 0 ) ( 2 ) x^{(1)}(2) = x^{(0)}(1) + x^{(0)}(2) x ( 1 ) ( 2 ) = x ( 0 ) ( 1 ) + x ( 0 ) ( 2 ) …
2. 构造背景值 (紧邻均值生成)
目的 :为建立微分方程模型做准备,用X ( 1 ) X^{(1)} X ( 1 ) Z ( 1 ) Z^{(1)} Z ( 1 )
z ( 1 ) ( k ) = 0.5 ( x ( 1 ) ( k ) + x ( 1 ) ( k − 1 ) ) , k = 2 , 3 , … , n z^{(1)}(k) = 0.5 (x^{(1)}(k) + x^{(1)}(k-1)), \quad k = 2, 3, \dots, n
z ( 1 ) ( k ) = 0.5 ( x ( 1 ) ( k ) + x ( 1 ) ( k − 1 )) , k = 2 , 3 , … , n
3. 建立灰色微分方程并求解参数
目的 :从离散的数据点中,提炼出能代表整体趋势的核心参数 a a a b b b 灰色微分方程 :
x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b x^{(0)}(k) + a z^{(1)}(k) = b
x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b
参数含义 :
a a a 发展系数 (Development Coefficient) 。决定了趋势发展的强度b b b 灰色作用量 (Grey Action Quantity) 。反映了数据的内生驱动力
求解 : 使用最小二乘法求解参数列向量 u ^ = [ a , b ] T \hat{u} = [a, b]^T u ^ = [ a , b ] T
Y = ( x ( 0 ) ( 2 ) x ( 0 ) ( 3 ) ⋮ x ( 0 ) ( n ) ) , B = ( − z ( 1 ) ( 2 ) 1 − z ( 1 ) ( 3 ) 1 ⋮ ⋮ − z ( 1 ) ( n ) 1 ) Y = \begin{pmatrix} x^{(0)}(2) \\ x^{(0)}(3) \\ \vdots \\ x^{(0)}(n) \end{pmatrix}, \quad
B = \begin{pmatrix} -z^{(1)}(2) & 1 \\ -z^{(1)}(3) & 1 \\ \vdots & \vdots \\ -z^{(1)}(n) & 1 \end{pmatrix}
Y = x ( 0 ) ( 2 ) x ( 0 ) ( 3 ) ⋮ x ( 0 ) ( n ) , B = − z ( 1 ) ( 2 ) − z ( 1 ) ( 3 ) ⋮ − z ( 1 ) ( n ) 1 1 ⋮ 1
u ^ = ( B T B ) − 1 B T Y \hat{u} = (B^T B)^{-1} B^T Y
u ^ = ( B T B ) − 1 B T Y
4. 建立预测模型 (白化方程)
目的 :将离散的灰色关系转化为连续的、可求解的微分方程,从而得到一个可以预测未来的“生长曲线”公式
白化方程 (时间的连续函数) :
d x ( 1 ) d t + a x ( 1 ) = b \frac{dx^{(1)}}{dt} + a x^{(1)} = b
d t d x ( 1 ) + a x ( 1 ) = b
求解方程得到预测公式 :
x ^ ( 1 ) ( k + 1 ) = ( x ( 0 ) ( 1 ) − b a ) e − a k + b a \hat{x}^{(1)}(k+1) = \left(x^{(0)}(1) - \frac{b}{a}\right) e^{-ak} + \frac{b}{a}
x ^ ( 1 ) ( k + 1 ) = ( x ( 0 ) ( 1 ) − a b ) e − ak + a b
该公式用于预测累加序列 在未来任意时刻的值
5. 累减还原 (IAGO)
目的 :将预测出的“累计总高度”还原为我们真正关心的“每日生长量”X ^ ( 1 ) \hat{X}^{(1)} X ^ ( 1 )
x ^ ( 0 ) ( 1 ) = x ( 0 ) ( 1 ) \hat{x}^{(0)}(1) = x^{(0)}(1) x ^ ( 0 ) ( 1 ) = x ( 0 ) ( 1 ) x ^ ( 0 ) ( k + 1 ) = x ^ ( 1 ) ( k + 1 ) − x ^ ( 1 ) ( k ) \hat{x}^{(0)}(k+1) = \hat{x}^{(1)}(k+1) - \hat{x}^{(1)}(k) x ^ ( 0 ) ( k + 1 ) = x ^ ( 1 ) ( k + 1 ) − x ^ ( 1 ) ( k )
这样就得到了原始序列的拟合值与预测值
模型检验
检验类型
检验对象
检验目的
检验性质
级比偏差检验 模型参数 a 决定的理论趋势 与 数据自身的演化趋势
评估模型的内部结构合理性
内部结构 检验
残差/后验差检验 最终预测值 x ^ ( 0 ) \hat{x}^{(0)} x ^ ( 0 ) x ( 0 ) x^{(0)} x ( 0 )
评估模型的最终预测精度
外部精度 检验
1. 级比偏差检验
计算单个级比偏差 ρ ( k ) \rho(k) ρ ( k )
ρ ( k ) = ∣ 1 − ( 1 − 0.5 a 1 + 0.5 a ) 1 σ ( k ) ∣ \rho(k) = \left| 1 - \left(\frac{1-0.5a}{1+0.5a}\right) \frac{1}{\sigma(k)} \right|
ρ ( k ) = 1 − ( 1 + 0.5 a 1 − 0.5 a ) σ ( k ) 1
a a a σ ( k ) = x ( 0 ) ( k − 1 ) x ( 0 ) ( k ) \sigma(k) = \frac{x^{(0)}(k-1)}{x^{(0)}(k)} σ ( k ) = x ( 0 ) ( k ) x ( 0 ) ( k − 1 )
计算平均级比偏差 ρ ˉ \bar{\rho} ρ ˉ
ρ ˉ = 1 n − 1 ∑ k = 2 n ρ ( k ) \bar{\rho} = \frac{1}{n-1} \sum_{k=2}^{n} \rho(k)
ρ ˉ = n − 1 1 k = 2 ∑ n ρ ( k )
评判标准:
平均级比偏差 ρ ˉ \bar{\rho} ρ ˉ
级别
< 0.1 < 0.1 < 0.1 优
< 0.2 < 0.2 < 0.2 合格
≥ 0.2 \ge 0.2 ≥ 0.2 不合格
2. 残差检验
目的 :直观判断模型对历史数据的拟合程度
Δ k = ∣ x ( 0 ) ( k ) − x ^ ( 0 ) ( k ) x ( 0 ) ( k ) ∣ \Delta_k = \left| \frac{x^{(0)}(k) - \hat{x}^{(0)}(k)}{x^{(0)}(k)} \right|
Δ k = x ( 0 ) ( k ) x ( 0 ) ( k ) − x ^ ( 0 ) ( k )
P 精度 = ( 1 − 1 n ∑ k = 1 n Δ k ) × 100 % P_{\text{精度}} = \left(1 - \frac{1}{n}\sum_{k=1}^{n} \Delta_k\right) \times 100\%
P 精度 = ( 1 − n 1 k = 1 ∑ n Δ k ) × 100%
平均相对精度
级别
> 90%
优
> 80%
良
> 70%
合格
< 70%
不合格
3. 后验差检验
目的 :更严格地从统计角度评估模型的泛化能力
计算原始序列方差 S 1 2 S_1^2 S 1 2 S 2 2 S_2^2 S 2 2
计算后验差比值 C :
C = S 2 S 1 C = \frac{S_2}{S_1}
C = S 1 S 2
计算小误差概率 P :
P = Prob ( ∣ 残差 ( k ) − 残差均值 ∣ < 0.6745 S 1 ) P = \text{Prob} (|\text{残差}(k) - \text{残差均值}| < 0.6745 S_1)
P = Prob ( ∣ 残差 ( k ) − 残差均值 ∣ < 0.6745 S 1 )
根据C值和P值,将模型精度分为四个等级:
精度等级
C 值
P 值
优 (一级) C ≤ 0.35 C \le 0.35 C ≤ 0.35 P ≥ 0.95 P \ge 0.95 P ≥ 0.95
合格 (二级) C ≤ 0.50 C \le 0.50 C ≤ 0.50 P ≥ 0.80 P \ge 0.80 P ≥ 0.80
勉强合格 (三级) C ≤ 0.65 C \le 0.65 C ≤ 0.65 P ≥ 0.70 P \ge 0.70 P ≥ 0.70
不合格 (四级) C > 0.65 C > 0.65 C > 0.65 P < 0.70 P < 0.70 P < 0.70
只有通过后验差检验(至少达到勉强合格)的模型,才能用于外推预测
优缺点与适用场景
优点
样本需求少 : 理论上4个数据点即可建模,非常适合数据稀疏的场景分布要求宽 : 不需要数据服从特定的统计分布(如正态分布)计算简单 : 相较于复杂的计量或机器学习模型,计算过程清晰、快捷短期预测准 : 对于具有明显单调(类指数)趋势的序列,短期预测效果好
缺点
适用范围窄 : 对波动性强、周期性或无明显趋势的序列效果很差中长期预测差 : 本质是指数拟合,预测期越长,误差累积越严重模型较敏感 : 原始数据的微小变动或新数据的加入可能导致模型参数变化较大
适用场景 数据量有限 的短期 、单调趋势 预测
社会经济 : 能源消耗、粮食产量、人口数量、特定商品价格的短期趋势管理决策 : 新产品销量、网站访问量、库存变化的短期预测地质水文 : 河流径流量、自然灾害发生次数的短期预测
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 import numpy as npimport matplotlib.pyplot as plt'font.sans-serif' ] = ['SimHei' ]'axes.unicode_minus' ] = False class GreyForecast :""" GM(1,1)灰色预测模型 该类实现了灰色预测的完整流程,包括级比检验、建模、预测和多维度检验。 """ def __init__ (self, data, n_preds ):""" 初始化模型 :param data: 原始数据序列 (list or numpy array) :param n_preds: 需要向后预测的期数 (int) """ if not isinstance (data, (list , np.ndarray)) or len (data) < 4 :raise ValueError("输入数据必须是列表或Numpy数组,且至少包含4个数据点。" )len (data)None def _level_ratio_test (self, data_series ):""" 执行级比检验 :param data_series: 需要检验的数据序列 :return: (bool, list) 是否通过检验,级比序列 """ 1 :] / data_series[:-1 ]2 / (self.n + 1 ))2 / (self.n + 1 ))all ((level_ratios > lower_bound) & (level_ratios < upper_bound))return passed, level_ratiosdef fit (self ):""" 执行建模与预测全流程 """ 0 if not test_passed:min () + 1 if not test_passed_after_translation:print ("警告:原始数据未通过级比检验,且平移变换后仍未通过。模型可能不适用。" )0.5 * (x1[:-1 ] + x1[1 :])1 :].reshape(-1 , 1 )0 ] = x0[0 ]for k in range (1 , total_len):0 ] - b / a) * np.exp(-a * k) + b / a0 ] = x0[0 ]1 :] = x1_fit_pred[1 :] - x1_fit_pred[:-1 ]if translation_c > 0 :"parameters" : {"a" : a, "b" : b},"translation_c" : translation_c,"fitted_values" : fitted_values,"predicted_values" : predicted_values,"tests" : testsreturn self.prediction_resultsdef _run_post_tests (self, original, fitted, a ):""" 执行所有建模后的检验 """ abs (residuals / original)1 - mean_relative_error1 )1 )1 )sum (np.abs (residuals - np.mean(residuals)) < 0.6745 * s1)1 - 0.5 * a) / (1 + 0.5 * a)abs (1 - theory_ratio / level_ratios[1 :]) return {"residual_test" : {"residuals" : residuals,"relative_errors" : relative_errors,"mean_relative_error" : mean_relative_error,"accuracy" : accuracy"posterior_error_test" : {"C_ratio" : C,"P_small_error_prob" : P"level_ratio_deviation_test" : {"mean_deviation" : mean_ratio_deviationdef plot (self ):""" 绘制结果图 """ if self.prediction_results is None :print ("请先调用 .fit() 方法进行建模。" )return 1 , self.n + 1 )1 , self.n + 1 )1 , self.n + self.n_preds + 1 )12 , 7 ))'o-' , label='原始数据 (Original Data)' , color='blue' )'fitted_values' ], 's--' , label='拟合数据 (Fitted Data)' ,'green' )'predicted_values' ], '^-' ,'预测数据 (Predicted Data)' , color='red' )'GM(1,1) 灰色预测模型结果' )'时间序列 (Time Series)' )'数值 (Value)' )True , linestyle='--' , alpha=0.6 )def print_results (self ):""" 格式化打印所有结果 """ if self.prediction_results is None :print ("请先调用 .fit() 方法进行建模。" )return print ("\n" + "=" * 50 )print ("GM(1,1) 灰色预测模型结果报告" )print ("=" * 50 )print ("\n[1] 级比检验结果" )2 / (self.n + 1 ))2 / (self.n + 1 ))print (f" - 级比检验区间: ({lower_bound:.4 f} , {upper_bound:.4 f} )" )print (f" - 原始数据级比检验: {'通过' if original_passed else '不通过' } " )print (f" - 级比序列: {[f'{ratio:.4 f} ' for ratio in original_ratios]} " )if res['translation_c' ] > 0 :'translation_c' ]print (f" - 平移变换后级比检验: {'通过' if transformed_passed else '不通过' } " )print (f" - 平移后级比序列: {[f'{ratio:.4 f} ' for ratio in transformed_ratios]} " )print ("\n[2] 模型参数" )print (f" - 发展系数 a = {res['parameters' ]['a' ]:.4 f} " )print (f" - 灰色作用量 b = {res['parameters' ]['b' ]:.4 f} " )if res['translation_c' ] > 0 :print (f" - 平移变换常数 c = {res['translation_c' ]:.4 f} " )print ("\n[3] 拟合与预测值" )for i, val in enumerate (res['fitted_values' ]):print (f" - 第 {i + 1 } 期 (拟合值): {val:.4 f} " )for i, val in enumerate (res['predicted_values' ]):print (f" - 第 {self.n + i + 1 } 期 (预测值): {val:.4 f} " )print ("\n[4] 模型检验结果" )'tests' ]['residual_test' ]['accuracy' ]print (f"\n--- 4.1 残差检验 ---" )print (f" - 平均相对误差: {1 - acc:.4 %} " )print (f" - 模型精度: {acc:.4 %} " )'tests' ]['posterior_error_test' ]['C_ratio' ]'tests' ]['posterior_error_test' ]['P_small_error_prob' ]"优" if C <= 0.35 else "合格" if C <= 0.50 else "勉强合格" if C <= 0.65 else "不合格" "优" if P >= 0.95 else "合格" if P >= 0.80 else "勉强合格" if P >= 0.70 else "不合格" print (f"\n--- 4.2 后验差检验 ---" )print (f" - 后验差比值 C = {C:.4 f} (等级: {c_level} )" )print (f" - 小误差概率 P = {P:.4 f} (等级: {p_level} )" )'tests' ]['level_ratio_deviation_test' ]['mean_deviation' ]"优" if rho < 0.1 else "合格" if rho < 0.2 else "不合格" print (f"\n--- 4.3 级比偏差检验 ---" )print (f" - 平均级比偏差 = {rho:.4 f} (等级: {rho_level} )" )print ("\n" + "=" * 50 )if __name__ == '__main__' :print ("--- 示例 1:典型增长数据 ---" )71.8 , 80.6 , 96.5 , 108.3 , 118.9 , 130.1 ]3 )print ("\n\n--- 示例 2:波动较大,不一定适用的示例 ---" )22 , 20 , 25 , 28 , 26 , 30 , 34 , 32 ]4 )
ARIMA 时间序列模型
ARIMA模型,全称为差分整合移动平均自回归模型 (Autoregressive Integrated Moving Average Model) ,是应用统计学中进行时间序列分析和预测的基石模型。它的核心思想是,一个时间序列中的数值变化规律可以通过其自身过去的值、过去的预测误差以及这两者的线性组合来捕捉和描述
该模型由三个核心参数(p, d, q)定义,每个字母都代表了模型的一个关键组成部分:
p (Autoregressive - AR) : 自回归阶数,指当前值与过去多少个观测值 直接相关d (Integrated - I) : 差分阶数,指为使序列变得平稳 所需要进行的差分运算次数q (Moving Average - MA) : 移动平均阶数,指当前值与过去多少个预测误差 直接相关
平稳性 (Stationarity)与差分
平稳性是ARIMA模型应用的先决条件。一个平稳的时间序列,其统计特性不随时间的推移而改变。具体来说,它应满足:
均值恒定 : 序列的平均水平不随时间改变方差恒定 : 序列的波动幅度不随时间改变(无异方差)自协方差不依赖于时间 : 序列在任意两个时间点t和t-k的关联性只取决于时间间隔k,而与t的位置无关
只有当序列的统计规律不随时间变化时,我们才能相信从历史数据中学到的模式(如均值、方差、自相关性)在未来同样适用,从而使预测成为可能
差分 是处理非平稳性的主要手段,其操作由参数d即差分次数 控制,具体为计算相邻观测值之差,一阶差分Y t ′ = Y t − Y t − 1 Y'_t = Y_t - Y_{t-1} Y t ′ = Y t − Y t − 1
判断是否平稳的方法:
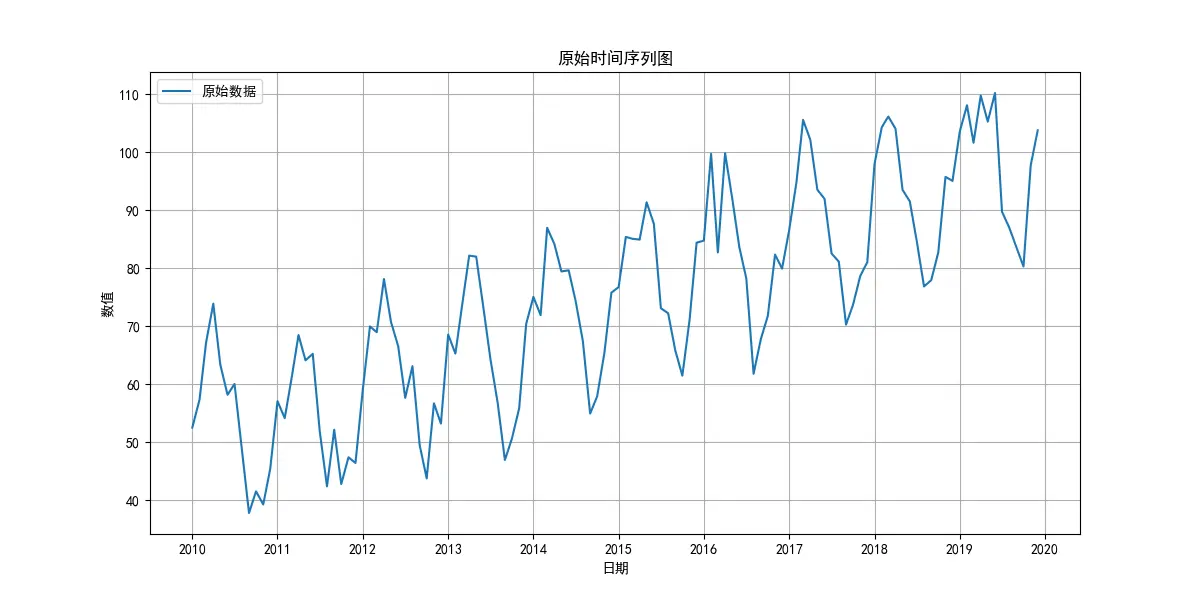
视觉判断: 观察时序图,如果存在明显趋势或季节性,则序列非平稳。
统计检验: 使用增强迪基-福勒检验 (Augmented Dickey-Fuller Test, ADF检验)
原假设 (H₀) : 序列存在单位根,即非平稳 检验目标 : 我们希望检验结果的p值小于0.05 ,这样就可以拒绝原假设,认为序列是平稳的
即对原始序列进行ADF检验。若不平稳,则进行差分,再对差分后的序列进行检验。重复此过程,直到检验通过。总共的差分次数就是d的值,d通常不超过2
模型构成
在序列通过差分变得平稳后,我们用AR和MA部分来对其中的动态结构进行建模
AR(p p p
描述当前值与过去值之间的线性关系,即“系统的记忆”
数学形式 :
Y t = c + ϕ 1 Y t − 1 + ϕ 2 Y t − 2 + ⋯ + ϕ p Y t − p + ϵ t Y_t = c + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \dots + \phi_p Y_{t-p} + \epsilon_t
Y t = c + ϕ 1 Y t − 1 + ϕ 2 Y t − 2 + ⋯ + ϕ p Y t − p + ϵ t
其中 ϕ \phi ϕ p p p
偏自相关函数图 (PACF) :衡量了在剔除中间所有滞后项的传递影响后,Y t Y_t Y t Y t − k Y_{t-k} Y t − k p p p 滞后第p p p (相关系数突然跌落至置信区间内并保持在其中)
MA(q q q
描述当前值与过去预测误差(随机冲击)之间的关系,即“冲击的记忆”。它不是 指滚动的平均值
数学形式 :
Y t = μ + ϵ t + θ 1 ϵ t − 1 + θ 2 ϵ t − 2 + ⋯ + θ q ϵ t − q Y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \dots + \theta_q \epsilon_{t-q}
Y t = μ + ϵ t + θ 1 ϵ t − 1 + θ 2 ϵ t − 2 + ⋯ + θ q ϵ t − q
其中 θ \theta θ q q q
自相关函数图 (ACF) :衡量了Y t Y_t Y t Y t − k Y_{t-k} Y t − k q q q 滞后第q q q
核心步骤
Box-Jenkins方法论是一个由四个步骤构成的、科学且迭代的建模框架
1. 模型识别 (Identification)
确定最合适的模型阶数( p , d , q ) (p, d, q) ( p , d , q )
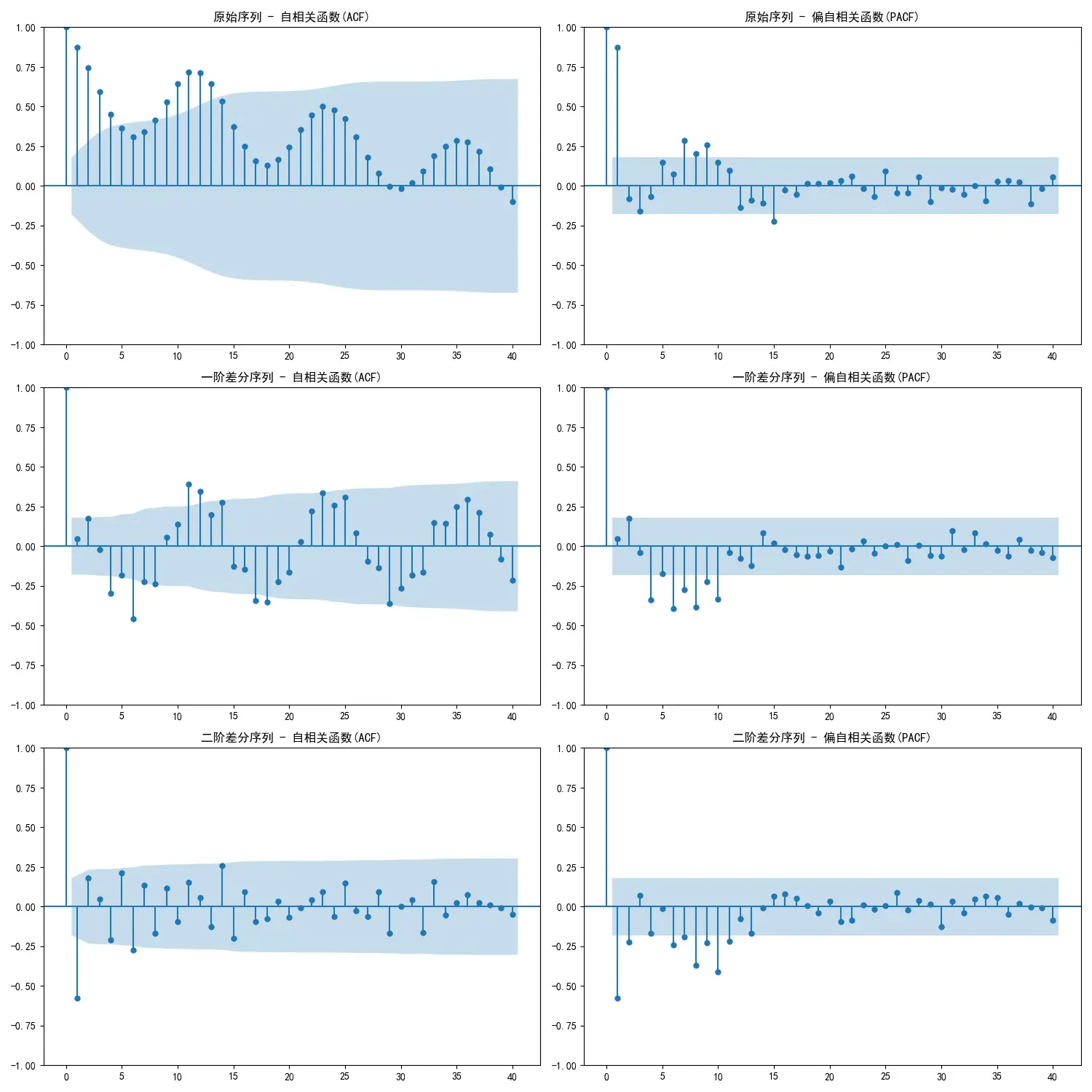
定 d d d : 通过ADF检验确定差分次数定 p p p q q q : 对差分后的平稳序列,绘制ACF和PACF图
PACF截尾,ACF拖尾 -> 考虑AR(p p p ( p , d , 0 ) (p, d, 0) ( p , d , 0 ) ACF截尾,PACF拖尾 -> 考虑MA(q q q ( 0 , d , q ) (0, d, q) ( 0 , d , q ) ACF和PACF均拖尾 -> 考虑ARMA(p , q p,q p , q ( p , d , q ) (p, d, q) ( p , d , q )
信息准则辅助 : 当图形特征不明显时,使用AIC(赤池信息量准则)或 BIC(贝叶斯信息量准则) ,但是需要在模型的拟合优度与复杂度之间做权衡,我们倾向于选择AIC或BIC值最小 的模型,BIC对模型复杂度的惩罚更重,因此更倾向于推荐简约模型
一般BIC效果更好,但是不能盲目根据AIC或BIC的结果之间确定模型,还应结合PACF和ACF图形进行判断
2. 参数估计 (Estimation)
在确定了模型结构( p , d , q ) (p,d,q) ( p , d , q ) ϕ \phi ϕ θ \theta θ c c c
最大似然估计 (Maximum Likelihood Estimation, MLE)
假定模型的误差项ϵ t \epsilon_t ϵ t
3. 模型诊断 (Diagnostic Checking)
对已估计好的模型进行“质检”,确保其充分捕捉了数据信息,通过检验模型的残差 (Residuals =真实值 - 预测值) 是否满足白噪声 的假定
诊断方法:
残差时序图 : 检查残差是否围绕0随机波动,且方差恒定残差ACF图 : 检查残差是否存在自相关。理想情况下,所有滞后阶数(lag>0)的柱子都应在置信区间内Ljung-Box Q检验 : 对残差的自相关性进行正式的统计检验
原假设(H 0 H_0 H 0 : 残差序列不存在自相关性判决 : 我们希望检验的p值 > 0.05 。一个大的p值意味着模型通过检验,残差是随机的
残差直方图/Q-Q图 : 检查残差是否服从正态分布,这对于预测区间的可靠性至关重要
迭代循环 : 若诊断检验失败(如Ljung-Box检验p值很小),必须返回第一步,重新识别模型(例如调整p p p q q q
4. 模型应用与预测 (Application & Forecasting)
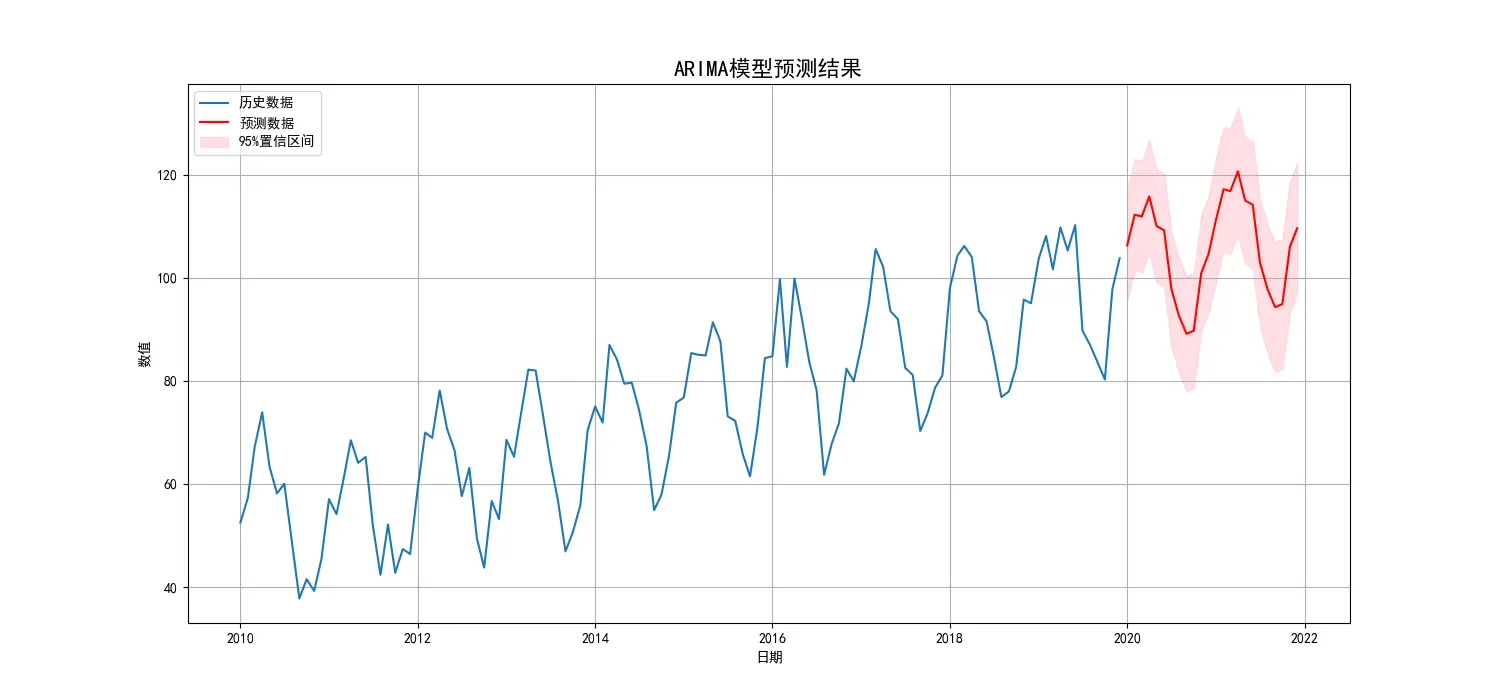
使用通过所有检验的最终模型来预测未来的数值,预测结果通常包含一个点预测 (最可能的值)和一个预测区间 (一个值范围)
随着预测时间向未来延伸,不确定性会累积,导致预测区间越来越宽。
ARIMA的局限与扩展模型
模型局限性
线性关系 : 只能捕捉线性规律,对于复杂的非线性模式无能为力单变量 : 传统ARIMA无法整合外部信息(如天气、政策、其他经济指标等)常数方差 : 假设误差的波动性是恒定的,不适用于金融市场等波动性聚集的场景
扩展模型
ARIMAX (ARIMA with eXogenous variables) : 在ARIMA模型中加入了外生解释变量,使得模型可以利用外部信息进行预测GARCH族模型 : 用于处理时变的波动性(异方差),常与ARIMA模型结合使用,先用ARIMA对收益率建模,再用GARCH对残差的波动性建模SARIMA (Seasonal ARIMA) : ARIMA( p , d , q ) ( P , D , Q ) m (p,d,q)(P,D,Q)_m ( p , d , q ) ( P , D , Q ) m
SARIMA:
基础ARIMA模型难以处理具有明显**季节性(Seasonality)**规律的时间序列。季节性指的是数据中以固定频率(如每年、每季度、每周)重复出现的模式。例如,零售业销售额通常在每年年底出现高峰
SARIMA模型的核心思想可以理解为两个ARIMA模型的巧妙结合 :一个用于描述短期非季节性动态,另一个用于描述长期季节性动态
它引入了四个新的季节性参数 :
m m m 季节性周期长度 。这是最重要的参数,它定义了“季节”的长度。对于月度数据,m = 12 m=12 m = 12 m = 4 m=4 m = 4 P P P 季节性自回归阶数 。表示当前值与过去季节的对应值(如Y t − m Y_{t-m} Y t − m Y t − 2 m Y_{t-2m} Y t − 2 m D D D 季节性差分阶数 。用于消除季节性趋势。其操作为:Y t ′ = Y t − Y t − m Y'_t = Y_t - Y_{t-m} Y t ′ = Y t − Y t − m Q Q Q 季节性移动平均阶数 。表示当前值与过去季节的预测误差(如ϵ t − m \epsilon_{t-m} ϵ t − m ϵ t − 2 m \epsilon_{t-2m} ϵ t − 2 m
一个完整的SARIMA模型表示为:
SARIMA ( p , d , q ) ( P , D , Q ) m \text{SARIMA}(p,d,q)(P,D,Q)_m
SARIMA ( p , d , q ) ( P , D , Q ) m
建模过程与Box-Jenkins方法论类似,但在识别阶段需要特别关注:
观察原始序列的ACF图,如果在大间隔的滞后(如m , 2 m , 3 m , … m, 2m, 3m, \dots m , 2 m , 3 m , …
先进行季节性差分(定D D D d d d
在平稳序列的ACF/PACF图上,观察滞后m , 2 m , … m, 2m, \dots m , 2 m , … P P P Q Q Q p p p q q q
代码示例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport statsmodels.api as smfrom statsmodels.tsa.stattools import adfullerfrom statsmodels.graphics.tsaplots import plot_acf, plot_pacffrom statsmodels.tsa.statespace.sarimax import SARIMAXimport pmdarima as pmimport warnings'ignore' , category=FutureWarning)'font.sans-serif' ] = ['SimHei' ]'axes.unicode_minus' ] = False def create_sample_data ():""" 创建一个带线性趋势和标准年度(12个月)季节性的模拟时间序列数据。 """ 42 )120 '2010-01-01' , periods=n_samples, freq='MS' )0 , 50 , n_samples)10 15 * np.sin(np.linspace(0 , n_years * 2 * np.pi, n_samples))0 , 5 , n_samples)50 + trend + seasonal + noise'value' )return ts_dataprint ("--- 数据预览 ---" )print (ts_data.head())print ("\n" )12 , 6 ))'原始数据' )'原始时间序列图' )'日期' )'数值' )True )def adf_test (timeseries ):""" 执行ADF检验并打印结果。 ADF检验的原假设(H0)是:序列存在单位根,即非平稳。 如果p-value < 0.05,我们拒绝原假设,认为序列是平稳的。 """ print ('--- ADF检验结果 ---' )'AIC' )print (f'ADF 统计量: {result[0 ]} ' )print (f'p-value: {result[1 ]} ' )print ('临界值:' )for key, value in result[4 ].items():print (f'\t{key} : {value} ' )if result[1 ] <= 0.05 :print ("结论: 序列是平稳的 (拒绝原假设)" )else :print ("结论: 序列是非平稳的 (无法拒绝原假设)" )print ("--- 对原始序列进行平稳性检验 ---" )print ("\n" )print ("--- 绘制ACF和PACF图进行模型识别 ---" )3 , 2 , figsize=(15 , 15 ))0 , 0 ], lags=40 , title='原始序列 - 自相关函数(ACF)' )0 , 1 ], lags=40 , title='原始序列 - 偏自相关函数(PACF)' )1 , 0 ], lags=40 , title='一阶差分序列 - 自相关函数(ACF)' )1 , 1 ], lags=40 , title='一阶差分序列 - 偏自相关函数(PACF)' )2 , 0 ], lags=40 , title='二阶差分序列 - 自相关函数(ACF)' )2 , 1 ], lags=40 , title='二阶差分序列 - 偏自相关函数(PACF)' )print ("--- 对一阶差分序列进行平稳性检验 ---" )print ("\n" )print ("--- 对二阶差分序列进行平稳性检验 ---" )print ("\n" )print ("--- 使用auto_arima自动寻找最优模型 ---" )1 , start_q=1 ,'adf' , 8 , max_q=8 , 12 , 1 , True , 0 ,None , True , 'ignore' ,True ,True , 'bic' )print ("\n--- 自动选择的最优模型摘要 ---" )print (model_fit.summary())print ("\n" )print ("--- 模型诊断 ---" )15 , 12 ))'模型诊断图' , fontsize=16 , y=0.92 )24 True )1 ] + pd.DateOffset(months=1 ), periods=n_periods, freq='MS' )'预测值' ])'置信下限' , '置信上限' ])print ("--- 未来24期预测结果 ---" )print (forecast_df)print ("\n--- 置信区间 ---" )print (conf_int_df)print ("\n" )15 , 7 ))'历史数据' )'预测数据' , color='red' )0 ],1 ], color='pink' , alpha=0.5 , label='95%置信区间' )'ARIMA模型预测结果' , fontsize=16 )'日期' )'数值' )'upper left' )True )
输出结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 --- 数据预览 ---to minimize bicBIC =853.299, Time =0.12 secBIC =853.166, Time =0.01 secBIC =837.517, Time =0.06 secBIC =849.036, Time =0.07 secBIC =848.701, Time =0.01 secBIC =857.678, Time =0.02 secBIC =830.314, Time =0.18 secBIC =818.295, Time =0.33 secBIC =813.706, Time =0.14 secBIC =848.818, Time =0.06 secBIC =818.221, Time =0.33 secBIC =848.207, Time =0.17 secBIC =inf, Time =0.63 secBIC =inf, Time =0.22 secBIC =814.285, Time =0.14 secBIC =inf, Time =0.54 secBIC =inf, Time =0.25 secBIC =inf, Time =0.37 secBIC =809.029, Time =0.11 secBIC =844.285, Time =0.04 secBIC =832.892, Time =0.03 secBIC =813.618, Time =0.27 secBIC =813.544, Time =0.24 secBIC =853.190, Time =0.01 secBIC =843.650, Time =0.11 secBIC =825.668, Time =0.11 secBIC =inf, Time =0.51 secBIC =inf, Time =0.22 secBIC =809.609, Time =0.12 secBIC =790.425, Time =0.15 secBIC =848.767, Time =0.07 secBIC =817.402, Time =0.08 secBIC =795.052, Time =0.26 secBIC =794.988, Time =0.29 secBIC =857.412, Time =0.02 secBIC =848.417, Time =0.22 secBIC =804.015, Time =0.22 secBIC =799.983, Time =0.40 secBIC =788.774, Time =0.09 secBIC =844.499, Time =0.04 secBIC =816.103, Time =0.06 secBIC =793.108, Time =0.20 secBIC =792.958, Time =0.25 secBIC =853.266, Time =0.01 secBIC =843.923, Time =0.14 secBIC =799.897, Time =0.15 secBIC =inf, Time =0.68 secBIC =790.859, Time =0.15 secBIC =795.032, Time =0.20 secNo . Observations: 120.. ... .
结果解读:
数据特性与预处理
原始序列 :经ADF检验 (p-value=0.99),原始序列为非平稳 时间序列,含有趋势或周期性。差分处理 :进行一阶差分 (d=1) 后,序列变得平稳 (p-value ≈ 1.42e-11),满足了ARIMA建模的前提
事实是在这个示例中差分可以被AR代替
最优模型选择
通过 auto_arima 自动寻优(基于BIC最小化原则),最终确定的最优模型为 SARIMAX(0, 1, 1)x(1, 0, 1, 12)
这是一个包含一阶差分 (d=1) 、一个移动平均项 (q=1) 的模型,还包含了强大的年度季节性结构 (m=12) ,由一个季节性自回归项 (P=1) 和一个季节性移动平均项 (Q=1) 共同驱动,ar.S.L12 系数 (0.9892) 极接近1,表明数据存在极强的年度周期性
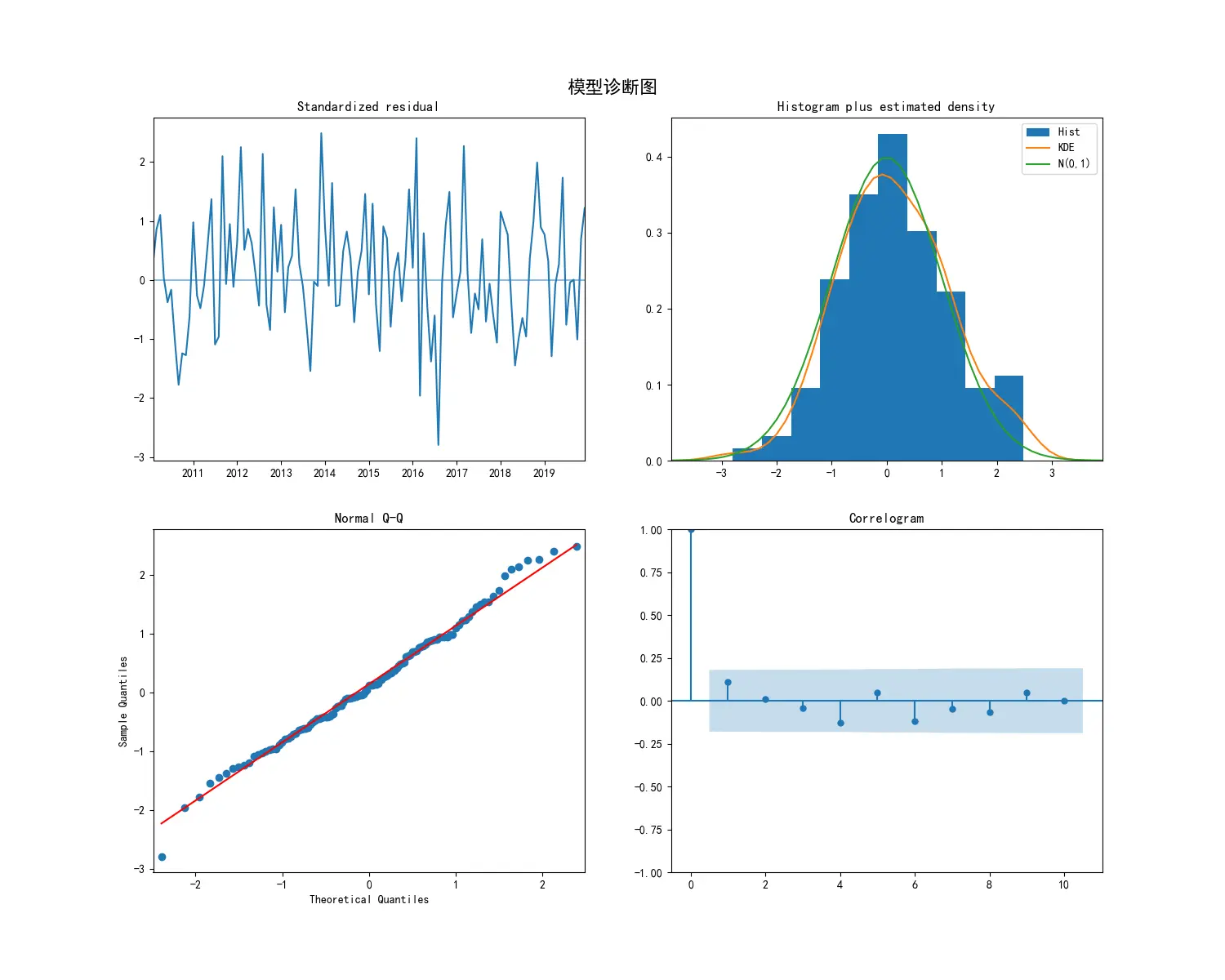
模型质量评估 (诊断检验)
残差独立性 (Ljung-Box) : Prob(Q) (0.23) > 0.05,表明残差为白噪声,模型已充分提取信息残差正态性 (Jarque-Bera) : Prob(JB) (0.89) > 0.05,表明残差服从正态分布残差方差齐性 (Heteroskedasticity) : Prob(H) (0.72) > 0.05,表明残差方差恒定所有模型系数的p-value均为0.000,统计上极其显著
朴素贝叶斯分类方法
朴素贝叶斯(Naive Bayes)是一种基于贝叶斯定理(Bayes’ Theorem)与特征条件独立性假设(Feature Conditional Independence Assumption)的概率分类算法。它以其简单、高效和在特定领域(尤其是文本分类)表现出奇的准确性而闻名
贝叶斯定理
贝叶斯定理是朴素贝叶斯算法的数学基石,它描述了在给定证据(特征)的情况下,一个假设(类别)的后验概率
其公式为:
P ( C ∣ X ) = P ( X ∣ C ) ⋅ P ( C ) P ( X ) P(C|X) = \frac{P(X|C) \cdot P(C)}{P(X)}
P ( C ∣ X ) = P ( X ) P ( X ∣ C ) ⋅ P ( C )
P ( C ∣ X ) P(C|X) P ( C ∣ X ) X X X C C C P ( X ∣ C ) P(X|C) P ( X ∣ C ) C C C X X X P ( C ) P(C) P ( C ) C C C P ( X ) P(X) P ( X ) X X X C C C P ( X ) P(X) P ( X )
分类决策的核心是,计算样本 X X X C k C_k C k
Predicted Class = arg max C k P ( C k ∣ X ) ∝ arg max C k P ( X ∣ C k ) ⋅ P ( C k ) \text{Predicted Class} = \arg\max_{C_k} P(C_k|X) \propto \arg\max_{C_k} P(X|C_k) \cdot P(C_k)
Predicted Class = arg C k max P ( C k ∣ X ) ∝ arg C k max P ( X ∣ C k ) ⋅ P ( C k )
“朴素”的特征条件独立性假设
这是该算法“朴素”(Naive)一词的来源。它假设:对于一个给定的类别,所有特征之间是相互独立的,互不影响
在独立性假设下,似然概率 P ( X ∣ C ) P(X|C) P ( X ∣ C )
P ( X ∣ C ) = P ( x 1 , x 2 , . . . , x n ∣ C ) = ∏ i = 1 n P ( x i ∣ C ) P(X|C) = P(x_1, x_2, ..., x_n|C) = \prod_{i=1}^{n} P(x_i|C)
P ( X ∣ C ) = P ( x 1 , x 2 , ... , x n ∣ C ) = i = 1 ∏ n P ( x i ∣ C )
其中 X = { x 1 , x 2 , . . . , x n } X=\{x_1, x_2, ..., x_n\} X = { x 1 , x 2 , ... , x n } n n n
核心步骤
准备阶段 :确定特征属性,并对训练样本进行分类训练阶段 :
计算每个类别的先验概率 P ( C k ) P(C_k) P ( C k )
计算每个类别下,每个特征属性的条件概率 P ( x i ∣ C k ) P(x_i|C_k) P ( x i ∣ C k )
分类阶段 :
对于一个新样本 X X X C k C_k C k P ( C k ) ∏ i = 1 n P ( x i ∣ C k ) P(C_k) \prod_{i=1}^{n} P(x_i|C_k) P ( C k ) ∏ i = 1 n P ( x i ∣ C k )
比较计算出的概率值,将样本归类到概率最大的那个类别
零概率问题与拉普拉斯平滑
问题 :如果在训练集中,某个特征值在某个类别下从未出现过,会导致其条件概率 P ( x i ∣ C k ) P(x_i|C_k) P ( x i ∣ C k )
拉普拉斯平滑 (Laplacian Smoothing) ,也称加一平滑。它对概率计算公式进行修正,确保任何概率值都不会为零
P ( x i ∣ C k ) = 类别 C k 中特征 x i 的出现次数 + α 类别 C k 的总样本数 + α ⋅ K P(x_i|C_k) = \frac{\text{类别 } C_k \text{ 中特征 } x_i \text{ 的出现次数} + \alpha}{\text{类别 } C_k \text{ 的总样本数} + \alpha \cdot K}
P ( x i ∣ C k ) = 类别 C k 的总样本数 + α ⋅ K 类别 C k 中特征 x i 的出现次数 + α
α \alpha α K K K x i x_i x i
主要模型类型
根据特征数据的分布类型,朴素贝叶斯主要分为三种模型:
高斯朴素贝叶斯 (Gaussian Naive Bayes)
适用场景 :特征是连续型数据(如身高、体重、温度),并假设这些特征在每个类别下都服从高斯(正态)分布方法 :对每个类别下的每个特征,计算其均值和方差。在预测时,使用高斯概率密度函数来计算条件概率 P ( x i ∣ C k ) P(x_i|C_k) P ( x i ∣ C k )
多项式朴素贝叶斯 (Multinomial Naive Bayes)
适用场景 :特征是离散型数据,通常表示“出现次数”或“频率”典型应用 :文本分类。特征是词汇表中的单词,值是该单词在文档中出现的次数(词频)
伯努利朴素贝叶斯 (Bernoulli Naive Bayes)
适用场景 :特征是二元(布尔)数据,即只关心特征“是否出现”典型应用 :文本分类。特征是词汇表中的单词,值是 1 或 0,表示该单词是否在文档中出现过
对立的特征可以直接转换成二元数据,如宽->1,窄->0
优缺点分析
优点
算法简单高效 :模型训练和预测的速度非常快,易于实现性能稳定 :对于小规模数据集,其表现通常很好,结果稳定对缺失数据不敏感 :在计算概率时,可以简单地忽略缺失的特征善于处理多分类问题 :在多分类任务中表现出色,且实现简单在特征独立的场景下效果最佳 :当数据满足其核心假设时,效果可与更复杂的模型媲美
缺点
特征条件独立性假设过强 :这个假设在现实世界中几乎不成立,是其主要理论缺陷。当特征之间关联性很强时,模型性能会下降对输入数据的表达形式敏感 :不同的数据预处理(如分箱、转换)可能会对结果产生较大影响先验概率影响 :在训练集不平衡时,先验概率可能会主导后验概率,导致对小样本类别的预测出现偏差
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 import numpy as npimport pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNB, MultinomialNB, BernoulliNBfrom sklearn.metrics import accuracy_score, classification_reportfrom sklearn.datasets import load_irisfrom sklearn.feature_extraction.text import CountVectorizerprint ("=" *60 )print ("示例 1: GaussianNB (高斯朴素贝叶斯) on Iris Dataset" )print ("=" *60 )'target' ] = yprint ("--- 数据集预览 (前5行) ---" )print (df.head())print ("\n标签含义: 0='setosa', 1='versicolor', 2='virginica'" )0.2 , random_state=42 )print (f"\n训练集大小: {X_train.shape} " )print (f"测试集大小: {X_test.shape} " )print ("\n--- 模型训练完成 ---" )print ("\n--- 预测结果 vs 真实结果 ---" )print ("预测结果:" , y_pred)print ("真实结果:" , y_test)print (f"\n模型准确率 (Accuracy): {accuracy:.4 f} " )print ("\n--- 分类报告 (Classification Report) ---" )print (classification_report(y_test, y_pred, target_names=iris.target_names))5.1 , 3.5 , 1.4 , 0.2 ]] 0 ]]print (f"\n--- 预测新样本 ---" )print (f"新样本 {new_flower} 的预测类别是: {predicted_class_name} ({prediction[0 ]} )" )print ("=" *60 )print ("示例 2: MultinomialNB (多项式朴素贝叶斯) for Text Classification" )print ("=" *60 )'A great game of football' ,'The election was close' ,'A very clean sweep in the game' ,'The president is speaking' ,'The player scored a goal' 'sports' , 'not sports' , 'sports' , 'not sports' , 'sports' ]print ("文本数据的词频特征 (供 MultinomialNB 使用):" )print (df_multi)print ("-" * 30 )print (f"\nMultinomialNB 模型准确率: {accuracy_mnb:.4 f} \n" )print ("MultinomialNB 分类报告:" )print (classification_report(labels, y_pred_mnb))'The team won the game' ]print (f"预测新句子 '{new_sentence_multi[0 ]} ' 的类别是: {prediction_mnb[0 ]} " )print ("\n\n" )print ("=" *60 )print ("示例 3: BernoulliNB (伯努利朴素贝叶斯) for Text Classification" )print ("=" *60 )True )print ("文本数据的二元特征 (供 BernoulliNB 使用):" )print (df_bern)print ("-" * 30 )print (f"\nBernoulliNB 模型准确率: {accuracy_bnb:.4 f} \n" )print ("BernoulliNB 分类报告:" )print (classification_report(labels, y_pred_bnb))'The president won the election' ]print (f"预测新句子 '{new_sentence_bern[0 ]} ' 的类别是: {prediction_bnb[0 ]} " )print ("\n\n" )
决策树
决策树是一种模拟人类决策过程的监督学习算法,可用于分类 和回归 任务。它通过学习一系列简单的是/否决策规则,从数据特征中推断出目标值,并将这个决策过程呈现为一棵树的形状
核心思想 :“分而治之 (Divide and Conquer)”。从根节点开始,通过对特征的提问,不断将数据集切分成更小的、特征更同质化的子集结构 :
根节点 (Root Node) :包含所有训练样本的起始点内部节点 (Internal Node) :代表一个特征的“问题”或“测试点”分支 (Branch) :代表对这个问题的不同“答案”叶节点 (Leaf Node) :代表最终的决策输出(一个类别或一个连续值)
一个生活中的例子:
根节点 :我要不要去打球?内部节点1 :天气怎么样?
如果是“雨天”,直接到达叶节点 :“不去”
如果是“晴天”,再进入内部节点2 :朋友去吗?
分支 :“去”、“不去”如果朋友“去”,到达叶节点 :“去!”
如果朋友“不去”,到达叶节点 :“不去”
决策树分类 (Classification Tree)
分类树的目标是预测一个离散的类别标签(如“是/否”)。CART (Classification and Regression Tree) 是最主流的实现算法,以下内容以其为例
除使用基尼不纯度 的CART,还有主要使用信息增益 的ID3的算法,和其改进版 - 使用信息增益率 作为划分标准的 C4.5算法,这里不多赘述
核心指标:基尼不纯度 (Gini Impurity)
CART使用基尼不纯度 来衡量一个节点的“混乱程度”,定义为从一个数据集中随机抽取两个样本,其类别标签不一致的概率 ,这个概率值越小,说明数据集越“纯净”,即数据集中大部分样本都属于同一个类别
G i n i ( D ) = 1 − ∑ i = 1 k p i 2 Gini(D) = 1 - \sum_{i=1}^{k} p_i^2
G ini ( D ) = 1 − i = 1 ∑ k p i 2
(其中 p i p_i p i
计算示例:
p y e s = 6 / 10 = 0.6 p_{yes} = 6/10 = 0.6 p yes = 6/10 = 0.6 p n o = 4 / 10 = 0.4 p_{no} = 4/10 = 0.4 p n o = 4/10 = 0.4 Gini = 1 − ( 0.6 2 + 0.4 2 ) = 1 − ( 0.36 + 0.16 ) = 1 − 0.52 = 0.48 1 - (0.6^2 + 0.4^2) = 1 - (0.36 + 0.16) = 1 - 0.52 = 0.48 1 − ( 0. 6 2 + 0. 4 2 ) = 1 − ( 0.36 + 0.16 ) = 1 − 0.52 = 0.48
这个0.48就代表了当前节点的混乱程度。如果10个样本全是“是”,Gini值将为 1 − ( 1 2 + 0 2 ) = 0 1 - (1^2 + 0^2) = 0 1 − ( 1 2 + 0 2 ) = 0
划分标准:基尼增益 (Gini Gain)
CART的目标是找到一个根据某个特征的某个切分点的划分,使得基尼不纯度下降得最多 。这个下降量被称为基尼增益 (Gini Gain)
G i n i _ G a i n = G i n i ( D f a t h e r ) − [ ∣ D l e f t ∣ ∣ D f a t h e r ∣ G i n i ( D l e f t ) + ∣ D r i g h t ∣ ∣ D f a t h e r ∣ G i n i ( D r i g h t ) ] Gini\_Gain = Gini(D_{father}) - \left[ \frac{|D_{left}|}{|D_{father}|} Gini(D_{left}) + \frac{|D_{right}|}{|D_{father}|} Gini(D_{right}) \right]
G ini _ G ain = G ini ( D f a t h er ) − [ ∣ D f a t h er ∣ ∣ D l e f t ∣ G ini ( D l e f t ) + ∣ D f a t h er ∣ ∣ D r i g h t ∣ G ini ( D r i g h t ) ]
计算示例: G i n i = 0.48 Gini=0.48 G ini = 0.48
划分数据 :
有房 (左节点) :5个样本,其中5个“是”,0个“否”。无房 (右节点) :5个样本,其中1个“是”,4个“否”。
计算子节点的Gini :
G i n i ( l e f t ) = 1 − ( 1 2 + 0 2 ) = 0 Gini(left) = 1 - (1^2 + 0^2) = 0 G ini ( l e f t ) = 1 − ( 1 2 + 0 2 ) = 0 G i n i ( r i g h t ) = 1 − ( ( 1 / 5 ) 2 + ( 4 / 5 ) 2 ) = 1 − ( 0.04 + 0.64 ) = 0.32 Gini(right) = 1 - ( (1/5)^2 + (4/5)^2 ) = 1 - (0.04 + 0.64) = 0.32 G ini ( r i g h t ) = 1 − (( 1/5 ) 2 + ( 4/5 ) 2 ) = 1 − ( 0.04 + 0.64 ) = 0.32
计算加权Gini :
加权Gini = ( 5 10 × 0 ) + ( 5 10 × 0.32 ) = 0 + 0.16 = 0.16 (\frac{5}{10} \times 0) + (\frac{5}{10} \times 0.32) = 0 + 0.16 = 0.16 ( 10 5 × 0 ) + ( 10 5 × 0.32 ) = 0 + 0.16 = 0.16
计算基尼增益 :
Gini Gain (是否有房) = 0.48 − 0.16 = 0.32 0.48 - 0.16 = 0.32 0.48 − 0.16 = 0.32
算法会为所有特征(如“是否有工作”、“年龄”等)都计算一遍基尼增益,然后选择增益最高的那个特征(如此处的“是否有房”)作为当前节点的划分标准
创建子节点与递归运行
在选定好特征来创建子节点时,CART通过二元切分 来处理所有类型的特征:
对于连续型特征:
处理方式与C4.5类似。将所有样本在该特征上的取值进行排序,然后遍历所有可能的切分点(通常是相邻两个值的中点),对每个切分点计算基尼增益,选择增益最大的那个点作为该特征的最佳二分点。例如,年龄 <= 30和年龄 > 30
对于离散型特征:
这是最能体现CART二分思想的地方。如果一个离散特征有N个取值(N > 2),CART会遍历该特征所有可能的取值组合,将其划分为两个子集,然后从中找到最佳的划分方式
举例说明: {北京, 上海, 广州}。CART在考虑如何用“城市”这个特征来分裂时,会评估以下所有可能的二分组合:
划分1: {北京} vs{上海, 广州}
划分2: {上海} vs {北京, 广州}
划分3: {广州}vs {北京, 上海}
CART会分别计算这三种划分方式的基尼增益,然后选择增益最大的那一种作为该节点的分裂方式。例如,如果划分1的基尼增益最大,那么该节点就会分裂成两条分支:“城市是北京”和“城市不是北京(即上海或广州)”
独热编码 (One-Hot Encoding):
用一个只包含0和1的稀疏向量来表示一个类别
示例:
原始数据:
经过独热编码后,会变成:
ID
城市_北京
城市_上海
城市_广州
1
1
0
0
2
0
1
0
3
0
0
1
现在,每个城市都被表示成一个向量,它们之间的距离是相等的,没有了顺序关系
实践中为了API的统一性、计算效率和工程上的便利,scikit-learn中的DecisionTreeClassifier被设计为只接受数值型输入。它内部并没有实现上述理论中那种复杂的、针对类别组合的搜索功能。它期望用户在将数据喂给它之前,就已经将所有非数值特征(如文本类别)转换完毕,因此使用热独编码
递归执行:
让每一个新的子节点,带着它所分配到的数据子集,返回第1步,重复整个过程,直到所有分支都达到停止条件
条件一(完全纯净):如果当前节点 D 中所有样本都属于同一类别,则无需再划分。将该节点标记为叶节点,类别即为该类别
条件二(特征用尽):如果所有可用的特征都已经被用于划分,但节点内的样本仍不属于同一类别,则也停止划分。将该节点标记为叶节点,其类别通常定为该节点中样本数最多的那个类别(少数服从多数)
条件三(样本集为空):如果划分到一个分支的样本集为空,则无法继续划分。将该节点标记为叶节点,其类别定为其父节点中样本数最多的类别
也可以人为设定条件进行剪枝,防止树过于庞大导致过拟合
预测
一个新的数据样本进入训练好的树,从根节点开始,根据每个节点的规则向下走,直到到达一个叶节点
决策树回归 (Regression Tree)
回归树的目标是预测一个连续的数值(如房价、气温)
核心指标:均方误差 (Mean Squared Error, MSE)
在分类树中,我们使用“信息熵”或“基尼不纯度”来衡量节点的“纯净度”。而回归树使用MSE 来衡量一个节点内样本值的“离散程度”。MSE本质上就是节点内样本目标值的方差 (Variance) ,MSE越小,节点内的数值越相似
M S E ( D ) = 1 N ∑ i = 1 N ( y i − y ˉ ) 2 MSE(D) = \frac{1}{N} \sum_{i=1}^{N} (y_i - \bar{y})^2
MSE ( D ) = N 1 i = 1 ∑ N ( y i − y ˉ ) 2
(其中 y ˉ \bar{y} y ˉ
划分标准:MSE缩减 (MSE Reduction)
回归树选择能够最大化MSE缩减量 的划分
M S E _ R e d u c t i o n = M S E ( D f a t h e r ) − [ N l e f t N f a t h e r M S E ( D l e f t ) + N r i g h t N f a t h e r M S E ( D r i g h t ) ] MSE\_Reduction = MSE(D_{father}) - \left[ \frac{N_{left}}{N_{father}} MSE(D_{left}) + \frac{N_{right}}{N_{father}} MSE(D_{right}) \right]
MSE _ R e d u c t i o n = MSE ( D f a t h er ) − [ N f a t h er N l e f t MSE ( D l e f t ) + N f a t h er N r i g h t MSE ( D r i g h t ) ]
计算示例:
计算根节点的MSE :
平均房价 y ˉ = ( 80 + 90 + 150 + 180 + 200 ) / 5 = 140 \bar{y} = (80+90+150+180+200)/5 = 140 y ˉ = ( 80 + 90 + 150 + 180 + 200 ) /5 = 140
M S E ( r o o t ) = 1 5 [ ( 80 − 140 ) 2 + . . . + ( 200 − 140 ) 2 ] = 1 5 [ 3600 + 2500 + 100 + 1600 + 3600 ] = 2280 MSE(root) = \frac{1}{5}[(80-140)^2 + ... + (200-140)^2] = \frac{1}{5}[3600+2500+100+1600+3600] = 2280 MSE ( roo t ) = 5 1 [( 80 − 140 ) 2 + ... + ( 200 − 140 ) 2 ] = 5 1 [ 3600 + 2500 + 100 + 1600 + 3600 ] = 2280
尝试以“面积 <= 100”为切分点 :
左节点 (面积<=100) : 样本{(70, 80), (80, 90)}右节点 (面积>100) : 样本{(120, 150), (140, 180), (160, 200)}
计算子节点的MSE :
左节点均值 y ˉ l e f t = ( 80 + 90 ) / 2 = 85 \bar{y}_{left} = (80+90)/2 = 85 y ˉ l e f t = ( 80 + 90 ) /2 = 85 M S E ( l e f t ) = 1 2 [ ( 80 − 85 ) 2 + ( 90 − 85 ) 2 ] = 25 MSE(left) = \frac{1}{2}[(80-85)^2 + (90-85)^2] = 25 MSE ( l e f t ) = 2 1 [( 80 − 85 ) 2 + ( 90 − 85 ) 2 ] = 25
右节点均值 y ˉ r i g h t = ( 150 + 180 + 200 ) / 3 ≈ 176.7 \bar{y}_{right} = (150+180+200)/3 \approx 176.7 y ˉ r i g h t = ( 150 + 180 + 200 ) /3 ≈ 176.7 M S E ( r i g h t ) = 1 3 [ ( 150 − 176.7 ) 2 + . . . ] ≈ 422.2 MSE(right) = \frac{1}{3}[(150-176.7)^2 + ...] \approx 422.2 MSE ( r i g h t ) = 3 1 [( 150 − 176.7 ) 2 + ... ] ≈ 422.2
计算MSE缩减量 :
加权MSE = ( 2 5 × 25 ) + ( 3 5 × 422.2 ) = 10 + 253.32 = 263.32 (\frac{2}{5} \times 25) + (\frac{3}{5} \times 422.2) = 10 + 253.32 = 263.32 ( 5 2 × 25 ) + ( 5 3 × 422.2 ) = 10 + 253.32 = 263.32
MSE缩减 = 2280 − 263.32 = 2016.68 2280 - 263.32 = 2016.68 2280 − 263.32 = 2016.68
算法会测试所有可能的切分点,选择使MSE缩减最大的那个点
创建子节点与递归运行
与决策树分类同理,当一个节点停止分裂时,它就成为一个叶节点。该叶节点的最终预测值,就是该节点内所有训练样本目标值的平均数
预测
一个新的数据样本进入树,最终会落在一个叶节点上。该样本的预测值就是这个叶节点中所有训练样本目标值的平均数 ,因此所有落到同一个叶节点上的样品的预测值都相同
预测示例: [面积 <= 100?] -> 是 -> 叶节点 (预测值=85万)
现在来了一个新数据:房屋面积为90平米 。
在根节点,判断“面积<=100”,答案是“是”
到达叶节点,该叶节点的预测值为85万。因此模型预测该房屋价格为85万
这也揭示了回归树预测的特点:预测值是分段常数 (Piecewise Constant)
剪枝:防止过拟合 (Pruning)
为了防止决策树学得“太细”(过拟合),需要进行剪枝
优缺点分析
优点
可解释性强 :模型逻辑清晰,可以被可视化和解释数据预处理要求低 :无需归一化或标准化能处理混合数据类型 :可以同时处理数值型和类别型数据自动进行特征选择 :建树过程天然地选出了重要性高的特征
缺点
容易过拟合 :单个决策树极易学习到训练数据中的噪声不稳定性 :数据的微小变动可能导致树结构发生巨大变化预测能力有限(回归) :回归树的预测不平滑,且无法进行外插(预测超出训练数据范围的值)局部最优问题 :采用贪心策略,不能保证得到全局最优树
多个决策树:集成学习 (Ensemble Learning)
为了克服单个决策树的缺点(尤其是不稳定性),现代机器学习通常将多个决策树组合起来,形成更强大的集成模型
随机森林 (Random Forest) :同时构建多棵树,每棵树使用随机的样本和特征子集。通过“集体投票”的方式进行预测,大大提高了模型的稳定性和准确性梯度提升决策树 (Gradient Boosted Decision Trees, GBDT) :按顺序构建多棵树,每一棵新树都努力去纠正前面所有树犯下的错误。像XGBoost、LightGBM等是其高效实现,是结构化数据上更先进强大的算法
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, plot_treefrom sklearn.datasets import load_iris, fetch_california_housingfrom sklearn.metrics import accuracy_score, classification_report, mean_squared_error, r2_score'font.sans-serif' ] = ['SimHei' , 'Heiti TC' , 'Microsoft JhengHei' ]'axes.unicode_minus' ] = False def run_classification_example ():""" 执行并展示决策树分类的示例。 任务:使用鸢尾花数据集 (Iris dataset) 进行品种分类。 """ print ("=" * 50 )print (" 示例1: 决策树分类 (鸢尾花数据集)" )print ("=" * 50 )print ("任务描述: 根据花的4个特征,预测其属于哪个品种。" )print ("特征名称:" , feature_names)print ("目标品种:" , class_names, "\n" )0.3 , random_state=42 , stratify=y)'gini' , max_depth=3 , random_state=42 )print ("开始训练决策树分类模型..." )print ("训练完成!\n" )print (f"决策树在测试集上的准确率: {accuracy:.4 f} \n" )print ("分类报告:" )print (classification_report(y_test, y_pred, target_names=class_names))20 , 12 ))True , True , 12 )"决策树分类可视化 (鸢尾花数据集, max_depth=3)" , fontsize=16 )def run_regression_example ():""" 执行并展示决策树回归的示例。 任务:使用加州房价数据集 (California Housing dataset) 预测房价。 """ print ("\n" * 3 )print ("=" * 50 )print (" 示例2: 决策树回归 (加州房价数据集)" )print ("=" * 50 )print ("任务描述: 根据地区的8个特征,预测房价中位数。" )print ("特征名称:" , feature_names, "\n" )0.3 , random_state=42 )4 , random_state=42 )print ("开始训练决策树回归模型..." )print ("训练完成!\n" )print (f"决策树在测试集上的均方误差(MSE): {mse:.4 f} " )print (f"决策树在测试集上的R^2决定系数: {r2:.4 f} \n" )10 , 6 ))0.5 , edgecolor='k' )min (), y_test.max ()], [y_test.min (), y_test.max ()], 'r--' , lw=2 )"真实房价" )"预测房价" )"决策树回归预测结果对比" , fontsize=16 )True )22 , 14 ))True ,True ,10 )"决策树回归结构可视化 (加州房价, max_depth=4)" , fontsize=16 )if __name__ == "__main__" :
随机森林
一种基于 决策树 (CART) 的 集成学习 (Ensemble Learning) 算法,通过构建了大量的决策树(即“森林”),通过集体决策(投票或平均)来提升模型的准确性和稳定性,有效克服单棵决策树容易过拟合的问题
两大随机性来源
随机森林的强大之处和名称来源在于其双重的随机性,这保证了“森林”中树木的多样性 和低相关性
样本随机 (行抽样 - Bagging)
做法 : 从包含N个样本的原始数据集中,有放回地 随机抽取N个样本,形成一个训练子集。这个过程重复M次,创建M个不同的训练集,用于训练M棵树目的 : 制造训练数据的多样性,使得每棵树都略有不同,从而降低整个模型的方差 (Variance) 副产品 : 每个训练过程中约有36.8%的数据未被抽中,称为袋外数据 (Out-of-Bag, OOB) ,可直接用于模型的验证,评估泛化能力
特征随机 (列抽样)
做法 : 在构建每棵决策树的每个节点 进行分裂时,不是从全部P个特征中选择最优分裂点,而是先随机选取p个特征 (通常p远小于P,例如 p ≈ P p \approx \sqrt{P} p ≈ P 目的 : 避免少数强特征主导所有决策树的构建,进一步降低树与树之间的相关性 (Correlation) ,增强模型的稳健性
核心步骤
训练阶段 :
a. 对原始数据集进行样本随机 抽样,得到训练集 D_i。
b. 使用 D_i 训练一棵决策树 T_i。在每个节点分裂时,都执行特征随机 选择
c. 通常让树完全生长,不进行剪枝
预测阶段 :
将新数据点输入到森林中所有的 n_estimators 棵树
得到 n_estimators 个预测结果
分类问题 : 采用投票 (Voting) 方式,得票最多的类别为最终结果回归问题 : 采用平均 (Averaging) 方式,所有树预测值的平均数为最终结果
关键超参数:
n_estimators: 森林中决策树的数量。数量越多,模型越稳定,但计算成本也越高,且性能提升有边际效应max_features: 在节点分裂时随机选择的特征数量。这是控制模型偏差和方差的关键参数,直接影响树之间的相关性max_depth: 树的最大深度。用于控制单棵树的复杂度,防止过拟合min_samples_split / min_samples_leaf: 节点分裂或叶节点所需的最小样本数,也用于控制树的生长
优缺点分析
优点
性能强大,准确率高 : 在绝大多数场景下,都是非常有效且强大的基线模型强抗过拟合能力 : 双重随机性使其比单棵决策树稳健得多能评估特征重要性 : 可以通过模型计算出每个特征对预测的贡献度易于并行化 : 每棵树的训练相互独立,计算效率高对缺失值不敏感 ,能处理高维度数据
缺点
模型解释性差 : 相对于单棵决策树清晰的规则,随机森林是一个“黑盒子 ”,难以解释具体预测的内在逻辑资源消耗大 : 当树的数量非常多时,训练和预测需要较大的内存和计算时间不适合某些类型数据 : 在处理非常稀疏的数据(如文本)时,可能不如专门的模型(如线性模型或梯度提升树)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as sns from sklearn.model_selection import train_test_splitfrom sklearn.ensemble import RandomForestClassifier, RandomForestRegressorfrom sklearn.datasets import load_iris, fetch_california_housingfrom sklearn.metrics import (accuracy_score, classification_report, confusion_matrix,from matplotlib.colors import ListedColormap'font.sans-serif' ] = ['SimHei' , 'Heiti TC' , 'Microsoft JhengHei' ]'axes.unicode_minus' ] = False "whitegrid" , font='SimHei' ) def plot_confusion_matrix (y_true, y_pred, class_names ):""" 绘制混淆矩阵热力图。 """ 8 , 6 ))True , fmt='d' , cmap='Blues' ,'混淆矩阵热力图' , fontsize=16 )'真实类别' , fontsize=12 )'预测类别' , fontsize=12 )def plot_decision_boundary (X, y, model, feature_names, class_names ):""" 绘制二维决策边界图。 注意:此函数仅为了可视化,只使用了两个最重要的特征。 """ 2 , 3 ]100 , random_state=42 , n_jobs=-1 ).02 0 ].min () - 0.5 , X_vis[:, 0 ].max () + 0.5 1 ].min () - 0.5 , X_vis[:, 1 ].max () + 0.5 10 , 7 ))'#FFAAAA' , '#AAFFAA' , '#AAAAFF' ])0.8 )0 ], X_vis[:, 1 ], c=y, cmap=ListedColormap(['#FF0000' , '#00FF00' , '#0000FF' ]),'k' , s=40 )'随机森林决策边界 (基于最重要的两个特征)' , fontsize=16 )0 ]], fontsize=12 )1 ]], fontsize=12 )0 ], labels=list (class_names), title="品种" )def run_iris_classifier_example ():""" 运行随机森林分类器的示例。 """ print ("=" * 50 )print (" 示例1: 鸢尾花分类 (Random Forest Classifier)" )print ("=" * 50 )print ("任务描述: 根据花的4个特征,预测其属于哪个品种。" )print ("特征名称:" , feature_names)print ("目标品种:" , class_names, "\n" )0.2 , random_state=42 , stratify=y)print (f"分类任务 - 训练集大小: {X_train.shape} " )print (f"分类任务 - 测试集大小: {X_test.shape} \n" )100 , random_state=42 , n_jobs=-1 )print ("开始训练鸢尾花分类模型..." )print ("训练完成!\n" )print (f"模型准确率 (Accuracy): {accuracy:.4 f} \n" )print ("分类报告 (Classification Report):\n" , classification_report(y_test, y_pred, target_names=class_names))False )12 , 7 ))"鸢尾花分类 - 特征重要性" , fontsize=16 )"重要性分数" , fontsize=12 )"特征" , fontsize=12 )def plot_residuals (y_true, y_pred ):""" 绘制残差图。 """ 10 , 6 ))0.5 )0 , color='r' , linestyle='--' )'残差图 (Residuals vs. Predicted Values)' , fontsize=16 )'预测值' , fontsize=12 )'残差 (真实值 - 预测值)' , fontsize=12 )def run_housing_regressor_example ():""" 运行随机森林回归器的示例。 """ print ("\n" * 3 )print ("=" * 50 )print (" 示例2: 加州房价预测 (Random Forest Regressor)" )print ("=" * 50 )print ("任务描述: 根据地区的8个特征,预测房价中位数。" )print ("特征名称:" , feature_names, "\n" )0.2 , random_state=42 )print (f"回归任务 - 训练集大小: {X_train.shape} " )print (f"回归任务 - 测试集大小: {X_test.shape} \n" )100 , random_state=42 , n_jobs=-1 )print ("开始训练加州房价预测模型..." )print ("训练完成!\n" )print (f"均方误差 (MSE): {mse:.4 f} " )print (f"R^2 决定系数: {r2:.4 f} \n" )False )12 , 7 ))"加州房价预测 - 特征重要性" , fontsize=16 )"重要性分数" , fontsize=12 )"特征" , fontsize=12 )10 , 6 ))0.3 , edgecolor='k' )min (), y_test.max ()], [y_test.min (), y_test.max ()], 'r--' , lw=2 , label='完美预测线' )'真实值 vs. 预测值' , fontsize=16 )'真实房价' , fontsize=12 )'预测房价' , fontsize=12 )True )if __name__ == "__main__" :
XGBoost
XGBoost 极致梯度提升 (eXtreme Gradient Boosting) 是梯度提升决策树 (GBDT) 的一种极致、高效、可扩展的工程实现。如果说随机森林是“民主投票制”(所有树独立并行工作),那么XGBoost就是“精英导师制”(每个新模型都在弥补前面模型的不足)
核心定位:处理结构化/表格数据 的非常有效的模型,在数据科学竞赛和工业界应用中被广泛使用
与随机森林的根本区别:
随机森林 (并行) :构建多棵独立的树,通过投票或平均来降低模型的方差,防止过拟合XGBoost (串行) :依次构建树,每一棵新树都旨在修正前面所有树的预测残差(误差),目标是不断降低模型的偏差,提升精度
XGBoost的原理建立在GBDT之上,并通过一系列优化达到了极致
基础思想:加法模型 (Additive Model)
y ^ i = ∑ k = 1 K f k ( x i ) \hat{y}_i = \sum_{k=1}^{K} f_k(x_i)
y ^ i = k = 1 ∑ K f k ( x i )
其中,K K K f k f_k f k k k k
学习目标:修正残差 (Residual Fitting) t − 1 t-1 t − 1 残差 error = y_true - y_predt t t f_t 的学习目标不再是原始的 y_true,而是这个 error。通过不断学习和累加修正残差的树,模型最终能很好地逼近真实值
“梯度”的体现:损失函数的梯度下降 损失函数关于当前预测值的负梯度 。这使得XGBoost可以支持任意可微的自定义损失函数,应用场景更广
XGBoost的“极致(eXtreme)”优化
正则化 (Regularization) :这是XGBoost防止过拟合的关键。它的目标函数包含了损失函数 和正则化项 两部分,在追求高精度的同时惩罚模型的复杂度,使其泛化能力更强二阶泰勒展开 :在优化目标函数时,XGBoost使用了二阶泰勒展开,同时利用了一阶导数(梯度)和二阶导数信息,使得优化过程更快、更准内置缺失值处理 :能自动学习和处理数据中的缺失值高效的工程实现 :支持大规模并行计算,优化了内存和缓存使用,训练速度远超传统GBDT
核心步骤
XGBoost (Extreme Gradient Boosting) 的核心在于其高度优化的目标函数和高效的树构建算法。整个推导过程可以分为四个主要部分:
定义模型与目标函数 :确定我们要优化的目标。泰勒展开近似 :将复杂的目标函数简化为二次函数。重构目标函数 :将对样本的优化,转为对树结构的优化。求解最优树 :推导如何计算叶子权重和如何寻找最佳分裂点。
1. 定义模型与目标函数
XGBoost是一个加法模型(Additive Model),由 K 棵树组成。对于第 i 个样本,其最终预测值 y ^ i \hat{y}_i y ^ i
y ^ i = ∑ k = 1 K f k ( x i ) \hat{y}_i = \sum_{k=1}^{K} f_k(x_i)
y ^ i = k = 1 ∑ K f k ( x i )
其中 f k f_k f k
这是一个逐步迭代的过程。在第 t 步,我们添加第 t 棵树 f t f_t f t
y ^ i ( t ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}_i^{(t)} = \hat{y}_i^{(t-1)} + f_t(x_i)
y ^ i ( t ) = y ^ i ( t − 1 ) + f t ( x i )
其中 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y ^ i ( t − 1 )
我们的总目标函数 (Objective Function) 由两部分组成:损失函数 和正则化项
Obj ( t ) = ∑ i = 1 n L ( y i , y ^ i ( t ) ) + ∑ k = 1 t Ω ( f k ) \text{Obj}^{(t)} = \sum_{i=1}^{n} L(y_i, \hat{y}_i^{(t)}) + \sum_{k=1}^{t} \Omega(f_k)
Obj ( t ) = i = 1 ∑ n L ( y i , y ^ i ( t ) ) + k = 1 ∑ t Ω ( f k )
L ( y i , y ^ i ( t ) ) L(y_i, \hat{y}_i^{(t)}) L ( y i , y ^ i ( t ) ) y ^ i ( t ) \hat{y}_i^{(t)} y ^ i ( t ) y i y_i y i ( y i − y ^ i ( t ) ) 2 (y_i - \hat{y}_i^{(t)})^2 ( y i − y ^ i ( t ) ) 2 Ω ( f k ) \Omega(f_k) Ω ( f k ) n n n
将 y ^ i ( t ) \hat{y}_i^{(t)} y ^ i ( t )
Obj ( t ) = ∑ i = 1 n L ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) \text{Obj}^{(t)} = \sum_{i=1}^{n} L(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t)
Obj ( t ) = i = 1 ∑ n L ( y i , y ^ i ( t − 1 ) + f t ( x i )) + Ω ( f t )
我们的目标是在第 t 步找到一棵树 f t f_t f t 最小化 这个 Obj ( t ) \text{Obj}^{(t)} Obj ( t )
2. 泰勒展开近似
目标函数中的 f t ( x i ) f_t(x_i) f t ( x i ) L L L 二阶泰勒展开 在 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y ^ i ( t − 1 )
一个通用的二阶泰勒展开公式为:
f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) ( Δ x ) 2 f(x + \Delta x) \approx f(x) + f'(x)\Delta x + \frac{1}{2} f''(x)(\Delta x)^2
f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x + 2 1 f ′′ ( x ) ( Δ x ) 2
我们将损失函数 L L L
x → y ^ i ( t − 1 ) x \rightarrow \hat{y}_i^{(t-1)} x → y ^ i ( t − 1 ) Δ x → f t ( x i ) \Delta x \rightarrow f_t(x_i) Δ x → f t ( x i )
应用展开,我们得到:
L ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) ≈ L ( y i , y ^ i ( t − 1 ) ) + ∂ L ( y i , y ^ i ( t − 1 ) ) ∂ y ^ i ( t − 1 ) ⋅ f t ( x i ) + 1 2 ⋅ ∂ 2 L ( y i , y ^ i ( t − 1 ) ) ∂ ( y ^ i ( t − 1 ) ) 2 ⋅ f t 2 ( x i ) \begin{aligned}
L\big(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)\big) \approx\
&L\big(y_i, \hat{y}_i^{(t-1)}\big)
+ \frac{\partial L(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)}} \cdot f_t(x_i)
+ \frac{1}{2} \cdot \frac{\partial^2 L(y_i, \hat{y}_i^{(t-1)})}{\partial (\hat{y}_i^{(t-1)})^2} \cdot f_t^2(x_i)
\end{aligned}
L ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) ≈ L ( y i , y ^ i ( t − 1 ) ) + ∂ y ^ i ( t − 1 ) ∂ L ( y i , y ^ i ( t − 1 ) ) ⋅ f t ( x i ) + 2 1 ⋅ ∂ ( y ^ i ( t − 1 ) ) 2 ∂ 2 L ( y i , y ^ i ( t − 1 ) ) ⋅ f t 2 ( x i )
为了简化,我们定义一阶导数(gradient)和 二阶导数(Hessian) :
g i = ∂ y ^ ( t − 1 ) L ( y i , y ^ i ( t − 1 ) ) g_i = \partial_{\hat{y}^{(t-1)}} L(y_i, \hat{y}_i^{(t-1)}) g i = ∂ y ^ ( t − 1 ) L ( y i , y ^ i ( t − 1 ) ) h i = ∂ y ^ ( t − 1 ) 2 L ( y i , y ^ i ( t − 1 ) ) h_i = \partial^2_{\hat{y}^{(t-1)}} L(y_i, \hat{y}_i^{(t-1)}) h i = ∂ y ^ ( t − 1 ) 2 L ( y i , y ^ i ( t − 1 ) )
在第 t 步,y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y ^ i ( t − 1 ) i i i g i g_i g i h i h_i h i 可以计算出的常数
将 g i g_i g i h i h_i h i f t f_t f t L ( y i , y ^ i ( t − 1 ) ) L(y_i, \hat{y}_i^{(t-1)}) L ( y i , y ^ i ( t − 1 ) ) 简化目标函数 :
Obj ( t ) ≈ ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) \text{Obj}^{(t)} \approx \sum_{i=1}^{n} \left[ g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i) \right] + \Omega(f_t)
Obj ( t ) ≈ i = 1 ∑ n [ g i f t ( x i ) + 2 1 h i f t 2 ( x i ) ] + Ω ( f t )
3. 重构目标函数(从样本到叶子)
现在,我们需要用数学语言来定义一棵树 f t f_t f t Ω ( f t ) \Omega(f_t) Ω ( f t )
树的定义 :一棵树由其结构 q q q w w w q ( x i ) q(x_i) q ( x i ) x i x_i x i j j j w j w_j w j j j j
f t ( x i ) = w q ( x i ) f_t(x_i) = w_{q(x_i)}
f t ( x i ) = w q ( x i )
正则化项定义 :复杂度由叶子的数量 T T T w w w
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega(f_t) = \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} w_j^2
Ω ( f t ) = γ T + 2 1 λ j = 1 ∑ T w j 2
其中 γ \gamma γ λ \lambda λ
将这两个定义代入简化目标函数:
Obj ( t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 \text{Obj}^{(t)} = \sum_{i=1}^{n} \left[ g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2 \right] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} w_j^2
Obj ( t ) = i = 1 ∑ n [ g i w q ( x i ) + 2 1 h i w q ( x i ) 2 ] + γ T + 2 1 λ j = 1 ∑ T w j 2
这个公式仍然是对所有样本 i i i 改变求和的顺序 ,将其重构为对叶子的求和
定义 I j = { i ∣ q ( x i ) = j } I_j = \{ i \mid q(x_i)=j \} I j = { i ∣ q ( x i ) = j } j j j
那么,对所有样本求和就等价于,先对所有叶子求和,再对每个叶子内的样本求和:
Obj ( t ) = ∑ j = 1 T [ ∑ i ∈ I j g i w j + ∑ i ∈ I j 1 2 h i w j 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 \text{Obj}^{(t)} = \sum_{j=1}^{T} \left[ \sum_{i \in I_j} g_i w_j + \sum_{i \in I_j} \frac{1}{2} h_i w_j^2 \right] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} w_j^2
Obj ( t ) = j = 1 ∑ T i ∈ I j ∑ g i w j + i ∈ I j ∑ 2 1 h i w j 2 + γ T + 2 1 λ j = 1 ∑ T w j 2
由于对于同一个叶子 j j j w j w_j w j
Obj ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \text{Obj}^{(t)} = \sum_{j=1}^{T} \left[ \left(\sum_{i \in I_j} g_i\right) w_j + \frac{1}{2} \left(\sum_{i \in I_j} h_i + \lambda \right) w_j^2 \right] + \gamma T
Obj ( t ) = j = 1 ∑ T i ∈ I j ∑ g i w j + 2 1 i ∈ I j ∑ h i + λ w j 2 + γ T
再次为了简化,我们定义每个叶子 j j j
G j = ∑ i ∈ I j g i G_j = \sum_{i \in I_j} g_i G j = ∑ i ∈ I j g i H j = ∑ i ∈ I j h i H_j = \sum_{i \in I_j} h_i H j = ∑ i ∈ I j h i
最终,我们得到了关于树结构的最终目标函数 :
Obj ( t ) = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \text{Obj}^{(t)} = \sum_{j=1}^{T} \left[ G_j w_j + \frac{1}{2} (H_j + \lambda) w_j^2 \right] + \gamma T
Obj ( t ) = j = 1 ∑ T [ G j w j + 2 1 ( H j + λ ) w j 2 ] + γ T
4. 求解最优树
这个最终的目标函数非常优美,它将问题分解成了两部分:
如何找到最优的树结构 (即如何分裂节点)?
对于一个固定的树结构 ,如何计算最优的叶子权重 w j w_j w j
求解最优叶子权重 w j ∗ w_j^* w j ∗
对于一个固定的树结构,每个叶子 j j j G j w j + 1 2 ( H j + λ ) w j 2 G_j w_j + \frac{1}{2} (H_j + \lambda) w_j^2 G j w j + 2 1 ( H j + λ ) w j 2 最优叶子权重 :
w j ∗ = − G j H j + λ w_j^* = - \frac{G_j}{H_j + \lambda}
w j ∗ = − H j + λ G j
将最优权重 w j ∗ w_j^* w j ∗ 评分(Score)
Obj ∗ = ∑ j = 1 T [ G j ( − G j H j + λ ) + 1 2 ( H j + λ ) ( − G j H j + λ ) 2 ] + γ T \text{Obj}^* = \sum_{j=1}^{T} \left[ G_j \left(- \frac{G_j}{H_j + \lambda}\right) + \frac{1}{2} (H_j + \lambda) \left(- \frac{G_j}{H_j + \lambda}\right)^2 \right] + \gamma T
Obj ∗ = j = 1 ∑ T [ G j ( − H j + λ G j ) + 2 1 ( H j + λ ) ( − H j + λ G j ) 2 ] + γ T
Obj ∗ = ∑ j = 1 T [ − G j 2 H j + λ + 1 2 G j 2 H j + λ ] + γ T \text{Obj}^* = \sum_{j=1}^{T} \left[ -\frac{G_j^2}{H_j + \lambda} + \frac{1}{2}\frac{G_j^2}{H_j + \lambda} \right] + \gamma T
Obj ∗ = j = 1 ∑ T [ − H j + λ G j 2 + 2 1 H j + λ G j 2 ] + γ T
Obj ∗ = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T \text{Obj}^* = - \frac{1}{2} \sum_{j=1}^{T} \frac{G_j^2}{H_j + \lambda} + \gamma T
Obj ∗ = − 2 1 j = 1 ∑ T H j + λ G j 2 + γ T
寻找最佳分裂点:分裂增益 (Gain)
XGBoost采用贪心算法来构建树。它从根节点开始,尝试所有可能的分裂,选择**增益(Gain)**最大的那个,增益的定义是:分裂后的收益减去分裂前的“收益”,再减去新增叶子带来的复杂度代价
增益 = (左子节点分数 + 右子节点分数) - 父节点分数 - γ \gamma γ
注意:这里的“分数”是指目标函数中与 w w w G , H G, H G , H − 1 2 G 2 H + λ -\frac{1}{2}\frac{G^2}{H+\lambda} − 2 1 H + λ G 2 γ \gamma γ T T T
设一个父节点为 P P P L L L R R R
Gain = ( − 1 2 G L 2 H L + λ ) + ( − 1 2 G R 2 H R + λ ) − ( − 1 2 G P 2 H P + λ ) − γ \text{Gain} = \left(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}\right) + \left(-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}\right) - \left(-\frac{1}{2}\frac{G_P^2}{H_P+\lambda}\right) - \gamma
Gain = ( − 2 1 H L + λ G L 2 ) + ( − 2 1 H R + λ G R 2 ) − ( − 2 1 H P + λ G P 2 ) − γ
整理后得到最终的分裂增益公式 :
Gain = 1 2 [ G L 2 H L + λ + G R 2 H R + λ − G P 2 H P + λ ] − γ \text{Gain} = \frac{1}{2} \left[ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{G_P^2}{H_P + \lambda} \right] - \gamma
Gain = 2 1 [ H L + λ G L 2 + H R + λ G R 2 − H P + λ G P 2 ] − γ
在构建树的每一步,算法都会遍历所有特征和所有可能的分裂点,计算其Gain值,并选择Gain最大的分裂方案。如果最大的Gain小于等于0,则停止分裂
总结:
初始化 :从深度为 0 的根节点开始,根节点包含所有训练样本。计算根节点的G root = ∑ i = 1 n g i G_{\text{root}} = \sum_{i=1}^n g_i G root = ∑ i = 1 n g i H root = ∑ i = 1 n h i H_{\text{root}} = \sum_{i=1}^n h_i H root = ∑ i = 1 n h i
迭代生长 :对于树中每一个尚未分裂的子节点,执行以下操作:
a. 设当前节点为 C C C G C 2 H C + λ \frac{G_C^2}{H_C + \lambda} H C + λ G C 2
b. 初始化 max_gain = 0 和 best_split = null
c. 遍历所有特征 :对数据中的每一个特征 k k k
i. 遍历所有分裂点 :对特征 k k k v v v
ii. 尝试分裂 :根据规则 $ \text{feature}_k < v $ 将当前节点 C C C I L I_L I L I R I_R I R
iii. 计算增益 :
计算 G L , H L , G R , H R G_L, H_L, G_R, H_R G L , H L , G R , H R
使用上面的分裂增益公式计算本次分裂的 Gain
如果 $ \text{Gain} > \text{max_gain} $,则更新 max_gain = Gain,并记录下当前的分裂特征和分裂点 v v v best_split
d. 决策 :在遍历完所有特征和所有分裂点后,如果 $ \text{max_gain} > 0 $,说明找到了一个可以带来收益的分裂点。就将当前节点 C C C best_split 的方案进行分裂,生成两个新的子节点
停止生长 :重复第 2 步,直到满足以下任一停止条件:
计算出的最大增益 max_gain 小于等于 0(或者小于一个用户设定的阈值 min_split_gain)。这意味着任何分裂都无法带来收益
树的深度达到了用户设定的最大深度 max_depth
叶子节点包含的样本权重之和(即 H H H min_child_weight。这可防止叶子节点样本太少,避免过拟合
总体流程
初始化模型,例如一个返回常数值的基模型
For t = 1 to K (迭代K棵树): i i i g i g_i g i h i h_i h i f t f_t f t f t f_t f t w j w_j w j w j ∗ = − G j H j + λ w_j^* = - \frac{G_j}{H_j + \lambda} w j ∗ = − H j + λ G j 更新总模型 :将新生成的树加入模型。通常会引入一个学习率 η \eta η 来防止过拟合:
y ^ i ( t ) = y ^ i ( t − 1 ) + η ⋅ f t ( x i ) \hat{y}_i^{(t)} = \hat{y}_i^{(t-1)} + \eta \cdot f_t(x_i)
y ^ i ( t ) = y ^ i ( t − 1 ) + η ⋅ f t ( x i )
结束迭代 ,得到最终的模型 y ^ = ∑ k = 1 K η ⋅ f k ( x i ) \hat{y} = \sum_{k=1}^K \eta \cdot f_k(x_i) y ^ = ∑ k = 1 K η ⋅ f k ( x i )
模型评估
交叉检验 (Cross-Validation)
这是一种更稳健、更可靠的评估方法。最常用的是K-折交叉验证 (K-Fold Cross-Validation)
将训练数据(不包括测试集)平均分成 K 份(例如 K=5 或 10)
进行 K 轮迭代。在每一轮中,选择其中 1 份作为验证集,其余 K-1 份作为训练集
训练模型并在验证集上计算评估指标
最终的评估结果是这 K 轮指标的平均值
分类任务核心评估指标
分类模型的评估指标可以从不同角度衡量其性能,通常需要综合考量
指标
核心含义
适用场景与解读
准确率 (Accuracy) 所有预测正确的样本占总样本的比例。
在类别均衡 的数据集上直观易懂。但在类别不均衡时具有极强的误导性 ,不推荐作为主要指标。
精确率 (Precision) “查准率” :在所有被预测为正例的样本中,真正是正例的比例。当误报(False Positive)的代价很高 时是关键指标。例如:垃圾邮件过滤(不想错杀好邮件)。
召回率 (Recall) “查全率” :在所有实际为正例的样本中,被成功预测出来的比例。当漏报(False Negative)的代价很高 时是关键指标。例如:疾病诊断(不想漏掉真病人)。
F1分数 (F1-Score) 精确率和召回率的调和平均数 。
当精确率和召回率同等重要,需要一个综合性指标 来平衡两者时使用。
AUC-ROC ROC曲线下的面积,衡量模型将正样本排在负样本前面的综合能力。
最常用、最重要的分类评估指标之一 。它不受类别不平衡和分类阈值选择的影响,能全面评估模型的排序能力。AUC越接近1越好,0.5代表随机猜测。
回归任务核心评估指标
回归模型的评估指标主要衡量预测值与真实值之间的数值差距
指标
核心含义
解读
MAE (平均绝对误差) 预测误差绝对值的平均数。
直观,单位与原数据相同,对异常值不敏感。
MSE (均方误差) 预测误差平方的平均数。
对大误差的惩罚比MAE更重。
RMSE (均方根误差) MSE的平方根。
最常用的回归指标 。单位与原数据相同,且对大误差敏感,易于解释。
R² (决定系数) 模型能解释的数据方差的比例。
值越接近1,说明模型对数据的拟合程度越好。
超参数与调参
无论使用何种工具,一个清晰的策略都至关重要。直接将所有参数扔给自动化工具不仅效率低下,而且结果可能不理想。推荐遵循以下结构化步骤,它能帮助你理解参数间的相互作用,并逐步优化模型
第0步:建立基准模型
目标 :确定一个合理的n_estimators(树的数量),为后续调优提供一个稳定的基准。做法 :
设置一个相对较高的学习率 learning_rate(如 0.1)。
使用一个较大的n_estimators(如 1000)。
利用**早停(Early Stopping)**机制,在验证集上监控性能。当验证集上的评估指标(如AUC, logloss等)在一定轮数内不再提升时,训练会自动停止。此时的迭代次数就是当前学习率下较优的n_estimators。
第1步:优化树的结构
目标 :调整对模型性能影响最大的参数,即树的复杂度和结构。参数 :max_depth, min_child_weight。
第2步:优化分裂阈值
目标 :通过调整分裂的“门槛”来进一步控制树的生长。参数 :gamma。
第3步:优化随机性
目标 :通过采样增加模型的随机性,降低过拟合风险。参数 :subsample, colsample_bytree。
第4步:优化正则化
目标 :对模型进行微调,进一步控制复杂度。参数 :reg_alpha, reg_lambda。
第5步:最终确定与降速
目标 :使用已找到的最优参数组合,通过降低学习率来训练一个更稳健、更精确的模型。做法 :将learning_rate降低(如从0.1降到0.01),同时按比例增加n_estimators(如增加10倍),再次使用早停确定最终的迭代次数。
网格搜索 (Grid Search)
网格搜索是最简单、最暴力的调参方法。它会尝试你指定参数的所有可能组合,通过为每个待调优的参数提供一个离散值的列表,网格搜索会遍历这些列表的所有组合,对每一种组合都训练一个模型并使用交叉验证进行评估,最终返回性能最好的参数组合
贝叶斯优化 (Bayesian Optimization)
贝叶斯优化是一种更智能、更高效的调参方法。它借鉴了先验知识来指导后续的搜索方向
即使使用自动化工具,也最好遵循前面提到的结构化策略 。例如,使用Optuna分阶段调整参数组,而不是一次性把所有参数都放进去优化,这样通常效果更好,也更易于分析
示例代码
建议在Jupyter环境下运行
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 import pandas as pdimport numpy as npimport xgboost as xgbimport optunaimport matplotlib.pyplot as pltimport seaborn as snstry :import shap True except ImportError:False print ("SHAP library is not available. Please install it with 'pip install shap'. Model explanation part will be skipped." )try :from optuna.visualization import plot_optimization_history, plot_param_importancesTrue except ImportError:False print ("Optuna visualization is not available. Please install it with 'pip install optuna-dashboard'." )from sklearn.datasets import load_iris, fetch_california_housingfrom sklearn.model_selection import train_test_split, cross_val_scorefrom sklearn.metrics import accuracy_score, confusion_matrix, classification_report, mean_squared_error, \def run_iris_classification ():""" 执行完整的鸢尾花分类XGBoost工作流, 包括使用Optuna进行自动化超参数调优和结果可视化。 """ print ("==========================================================" )print ("= Running XGBoost for Iris Multi-Class Classification =" )print ("==========================================================" )print (f"Iris dataset loaded. Shape: {X.shape} , Number of classes: {len (np.unique(y))} \n" )0.2 , random_state=42 , stratify=y)def objective_iris (trial ):"""定义Optuna要优化的目标函数。""" 'objective' : 'multi:softprob' ,'num_class' : 3 ,'eval_metric' : 'mlogloss' ,'verbosity' : 0 ,'booster' : 'gbtree' ,'tree_method' : 'hist' , 'lambda' : trial.suggest_float('lambda' , 1e-8 , 1.0 , log=True ),'alpha' : trial.suggest_float('alpha' , 1e-8 , 1.0 , log=True ),'max_depth' : trial.suggest_int('max_depth' , 2 , 7 ),'eta' : trial.suggest_float('eta' , 0.01 , 0.3 , log=True ),'subsample' : trial.suggest_float('subsample' , 0.5 , 1.0 ),'colsample_bytree' : trial.suggest_float('colsample_bytree' , 0.5 , 1.0 ),5 , scoring='accuracy' , n_jobs=-1 ).mean()return scoreprint ("--- Starting Hyperparameter Tuning with Optuna ---" )'maximize' )50 )print ("\nIris Tuning Finished!" )print (f"Best CV Accuracy: {study_iris.best_value:.4 f} " )print ("Best Hyperparameters:" , best_params_iris)if is_optuna_viz_available:print ("\n--- Visualizing Tuning Process ---" )"Iris: Optimization History" ).show()"Iris: Hyperparameter Importances" ).show()print ("\n--- Training Final Model on Full Training Data ---" )'multi:softprob' ,3 ,'mlogloss' ,'hist' ,print ("\n--- Evaluating Final Model on Test Set ---" )print (f"Test Set Accuracy: {accuracy_iris:.4 f} " )10 , 6 ))"Iris: Feature Importance" )8 , 6 ))True , fmt='d' , cmap='Blues' , xticklabels=iris.target_names, yticklabels=iris.target_names)'Predicted Label' )'True Label' )'Iris: Confusion Matrix' )print ("\nClassification Report:" )print (classification_report(y_test, y_pred_iris, target_names=iris.target_names))if not is_shap_available:print ("\n❌ SHAP库不可用,跳过模型解释分析" )return print ("\n--- SHAP Model Explanation Analysis ---" )print ("正在准备SHAP分析模型..." )'multi:softprob' , num_class=3 , eval_metric='mlogloss' ,'hist' , **best_params_irisprint ("正在计算SHAP值..." )100 , random_state=42 )print ("\n正在生成 SHAP 多分类汇总图 (Beeswarm)..." )print ("\n正在生成 SHAP 特征重要性条形图..." )"bar" ,False )"Iris: SHAP Feature Importance (Mean Absolute SHAP Values)" )print ("\n--- Individual Sample SHAP Analysis ---" )0 , 5 , 10 ]for i, idx in enumerate (sample_indices):print (f"\n分析测试样本 {idx} :" )print (f" 真实标签: {iris.target_names[y_test_sample[i]]} " )print (f" 预测标签: {iris.target_names[y_pred_sample_cpu[i]]} " )print (f" 为预测类别 '{iris.target_names[pred_class]} ' 生成力图..." )True , show=True ,10 )def run_california_housing_regression ():""" 执行完整的加州房价预测XGBoost工作流, 包括使用Optuna进行自动化超参数调优和结果可视化。 """ print ("\n\n==========================================================" )print ("= Running XGBoost for California Housing Price Prediction =" )print ("==========================================================" )print (f"California Housing dataset loaded. Shape: {X.shape} \n" )0.2 , random_state=42 )def objective_housing (trial ):""" 定义Optuna要优化的目标函数。 """ 'objective' : 'reg:squarederror' ,'eval_metric' : 'rmse' ,'verbosity' : 0 ,'booster' : 'gbtree' ,'tree_method' : 'hist' , 'lambda' : trial.suggest_float('lambda' , 1e-8 , 10.0 , log=True ),'alpha' : trial.suggest_float('alpha' , 1e-8 , 10.0 , log=True ),'max_depth' : trial.suggest_int('max_depth' , 3 , 10 ),'eta' : trial.suggest_float('eta' , 0.01 , 0.3 , log=True ),'subsample' : trial.suggest_float('subsample' , 0.6 , 1.0 ),'colsample_bytree' : trial.suggest_float('colsample_bytree' , 0.6 , 1.0 ),5 , scoring='neg_root_mean_squared_error' , n_jobs=-1 ).mean()return scoreprint ("--- Starting Hyperparameter Tuning with Optuna ---" )'maximize' )50 )print ("\nHousing Tuning Finished!" )print (f"Best CV RMSE: {-study_housing.best_value:.4 f} " )print ("Best Hyperparameters:" , best_params_housing)if is_optuna_viz_available:print ("\n--- Visualizing Tuning Process ---" )"Housing: Optimization History" ).show()"Housing: Hyperparameter Importances" ).show()print ("\n--- Training Final Model on Full Training Data ---" )'reg:squarederror' ,'rmse' ,'hist' ,print ("\n--- Evaluating Final Model on Test Set ---" )print (f"Root Mean Squared Error (RMSE): {rmse:.4 f} " )print (f"Mean Absolute Error (MAE): {mae:.4 f} " )print (f"R-squared (R²): {r2:.4 f} " )10 , 6 ))"Housing: Feature Importance" )10 , 10 ))0.5 )min (y_test), max (y_test)], [min (y_test), max (y_test)], '--' , color='red' , linewidth=2 )'Actual Prices ($100,000s)' )'Predicted Prices ($100,000s)' )'Housing: Actual vs. Predicted Prices' )'equal' )'square' )if not is_shap_available:print ("\n❌ SHAP库不可用,跳过模型解释分析" )return print ("\n--- SHAP Model Explanation Analysis ---" )print ("正在准备SHAP分析模型..." )'reg:squarederror' , eval_metric='rmse' ,'hist' , **best_params_housingprint ("正在计算SHAP值..." )200 , random_state=42 )print ("\n正在生成 SHAP 汇总图 (Beeswarm)..." )False )"Housing: SHAP Summary Plot - Feature Impact on Predictions" )print ("\n正在生成 SHAP 特征重要性条形图..." )"bar" , show=False )"Housing: SHAP Feature Importance (Mean Absolute SHAP Values)" )print ("\n--- Individual Sample SHAP Analysis ---" )0 , 1 , 2 ]for i, idx in enumerate (sample_indices):print (f"\n分析测试样本 {idx} :" )print (f" 真实房价: ${y_test_sample[i]:.2 f} (万美元)" )print (f" 预测房价: ${y_pred_sample[i]:.2 f} (万美元)" )print (f" 为样本 {idx} 生成瀑布图..." )True )print (f" 为样本 {idx} 生成力图..." )True , show=True )try :print ("\n--- Feature Interaction Analysis ---" )print ("正在生成 MedInc 的依赖图,并根据 HouseAge 着色..." )"MedInc" ],"HouseAge" ],True )except Exception as e:print (f"特征交互分析失败: {e} " )if __name__ == '__main__' :
k-近邻算法(KNN)
k-近邻(kNN)算法是监督学习中最简单、最直观的算法之一。它是一种“懒惰学习”(Lazy Learning)或基于实例的学习(Instance-based Learning)方法,本身没有显式的训练过程。
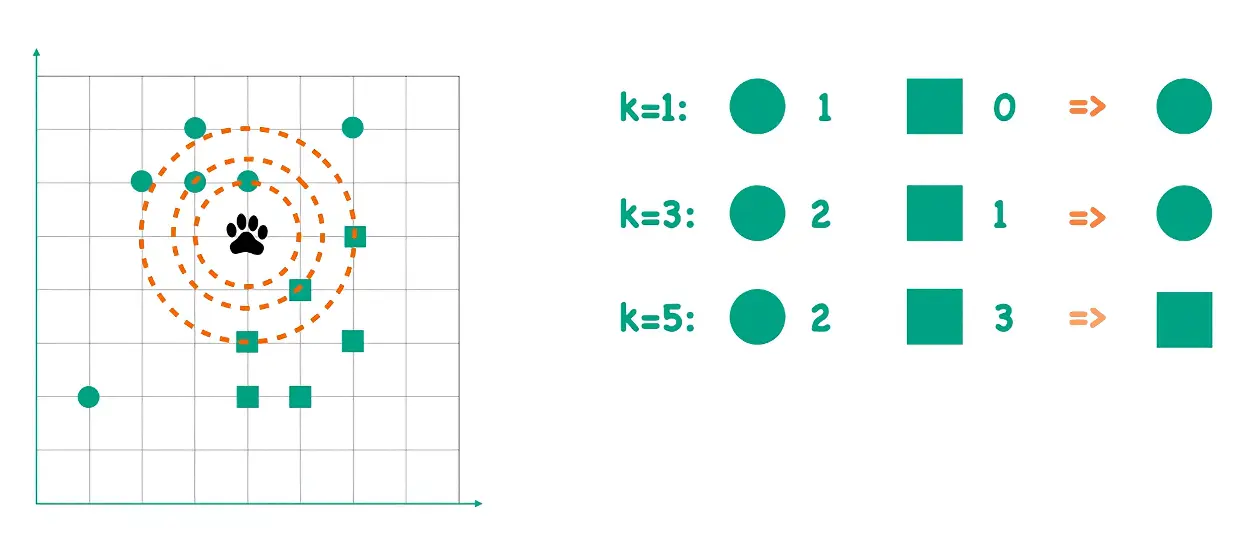
其核心思想为对于一个未知样本的分类,可以观察其在特征空间中最近的k个邻居,并由这些邻居的类别通过多数表决的方式来决定该样本的类别
这个思想可以应用于两个主要的机器学习任务:
分类(Classification) :新样本的类别由其k个最近邻居中出现次数最多的类别 (即众数)决定回归(Regression) :新样本的预测值是其k个最近邻居的数值的平均值或中位数
核心步骤
kNN算法的实现过程非常清晰,可以分为以下几个步骤:
先要对特征归一化 或标准化
确定关键参数 :
k值 :选择一个正整数k,代表要观察的最近邻居的数量距离度量 :选择一种计算样本之间距离的方法(如欧几里得距离)
k 太小容易过拟合,k 太大容易欠拟合,一般 k ≤ N k \le \sqrt{N} k ≤ N 交叉验证 等方法确定最优值
欧几里得距离(Euclidean Distance):A = ( x 1 , x 2 , . . . , x n ) A=(x_1, x_2, ..., x_n) A = ( x 1 , x 2 , ... , x n ) B = ( y 1 , y 2 , . . . , y n ) B=(y_1, y_2, ..., y_n) B = ( y 1 , y 2 , ... , y n )
$$
D(A, B) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}
$$
曼哈顿距离(Manhattan Distance):
D ( A , B ) = ∑ i = 1 n ∣ x i − y i ∣ D(A, B) = \sum_{i=1}^{n} |x_i - y_i|
D ( A , B ) = i = 1 ∑ n ∣ x i − y i ∣
闵可夫斯基距离(Minkowski Distance):
D ( A , B ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 p D(A, B) = \left( \sum_{i=1}^{n} |x_i - y_i|^p \right)^{\frac{1}{p}}
D ( A , B ) = ( i = 1 ∑ n ∣ x i − y i ∣ p ) p 1
当 p = 1 p=1 p = 1
当 p = 2 p=2 p = 2
计算距离 :
对于一个待预测的新样本,计算它与训练数据集中每一个 样本之间的距离
找到k个最近邻 :
将计算出的所有距离进行排序,找出距离最小的前k个样本,这些样本就是新样本的“k个最近邻”
做出决策 :
对于分类任务 :统计这k个邻居的类别。选择出现频率最高的类别作为新样本的预测类别。为避免平票,k通常取奇数对于回归任务 :计算这k个邻居的目标值的平均值(或其他聚合值,如中位数),将该平均值作为新样本的预测值
优缺点分析
优点
简单直观 :算法原理简单,易于理解和实现无需训练 :kNN是一种懒惰学习算法,没有显式的训练阶段,数据可以直接用于预测。这使得它可以轻松适应新数据非参数模型 :对数据分布没有假设,适用于各种复杂和非线性的决策边界对异常值不敏感 (在k值较大时)
缺点
计算成本高 :在预测阶段,需要计算待测样本与所有训练样本的距离,当训练集非常大时,计算量巨大,效率低下内存消耗大 :需要存储全部训练数据集对不相关特征和数据维度敏感 :在高维空间中,点之间的距离变得难以区分(所谓的**“维度灾难”**),不相关的特征会严重干扰距离计算,导致算法性能下降样本不均衡问题 :如果某些类别的样本数量远多于其他类别,那么新样本很容易被归类到这些多数类中
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 import matplotlib.pyplot as pltimport numpy as npimport seaborn as snsfrom collections import Counterfrom matplotlib.colors import ListedColormapfrom sklearn.neighbors import KNeighborsClassifierdef visualize_knn_process ():""" 一个完整的函数,用于分步可视化kNN算法的决策过程。 """ "whitegrid" )'font.sans-serif' ] = ['SimHei' ] 'axes.unicode_minus' ] = False 10 , 2 ], [12 , 1 ], [15 , 0 ], [9 , 3 ], [11 , 2 ]])1 , 10 ], [3 , 12 ], [0 , 9 ], [2 , 8 ], [4 , 11 ]])'动作片' ] * len (action_movies) + ['喜剧片' ] * len (comedy_movies)7 , 6 ])10 , 7 ))0 ], action_movies[:, 1 ], c='red' , s=100 , label='动作片 (Action)' )0 ], comedy_movies[:, 1 ], c='blue' , s=100 , label='喜剧片 (Comedy)' )'步骤 1: 已知的电影数据' , fontsize=16 )'爆炸场景数量' , fontsize=12 )'搞笑桥段数量' , fontsize=12 )True )10 , 7 ))0 ], action_movies[:, 1 ], c='red' , s=100 , label='动作片 (Action)' )0 ], comedy_movies[:, 1 ], c='blue' , s=100 , label='喜剧片 (Comedy)' )0 ], new_movie[1 ], c='grey' , s=250 , marker='*' , label='未知电影' , edgecolors='black' )'步骤 2: 出现一个未知的新电影' , fontsize=16 )'爆炸场景数量' , fontsize=12 )'搞笑桥段数量' , fontsize=12 )True )sum ((all_movies - new_movie) ** 2 , axis=1 ))3 10 , 7 ))0 ], action_movies[:, 1 ], c='red' , s=100 , alpha=0.3 )0 ], comedy_movies[:, 1 ], c='blue' , s=100 , alpha=0.3 )0 ], new_movie[1 ], c='grey' , s=250 , marker='*' , label='未知电影' , edgecolors='black' )0 ], nearest_neighbors[:, 1 ], s=150 ,'none' , edgecolors='green' , linewidth=3 , label=f'最近的 {k} 个邻居' )for neighbor in nearest_neighbors:0 ], neighbor[0 ]], [new_movie[1 ], neighbor[1 ]], 'g--' )f'步骤 3: K={k} , 寻找最近的{k} 个邻居' , fontsize=16 )'爆炸场景数量' , fontsize=12 )'搞笑桥段数量' , fontsize=12 )True )for i in nearest_indices]1 )[0 ][0 ]'blue' if final_decision == '喜剧片' else 'red' 10 , 7 ))0 ], action_movies[:, 1 ], c='red' , s=100 , alpha=0.3 )0 ], comedy_movies[:, 1 ], c='blue' , s=100 , alpha=0.3 )0 ], new_movie[1 ], c=final_color, s=250 , marker='*' ,f'最终分类: {final_decision} ' , edgecolors='black' )0 ], nearest_neighbors[:, 1 ], s=150 ,'none' , edgecolors='green' , linewidth=3 )"投票结果:\n" for label, count in vote_result.items():f"{label} : {count} 票\n" 0.5 , 6 , vote_text, fontsize=14 , bbox=dict (facecolor='yellow' , alpha=0.5 ))f'步骤 4: 邻居投票决定 (K={k} ),结果为 {final_decision} ' , fontsize=16 )'爆炸场景数量' , fontsize=12 )'搞笑桥段数量' , fontsize=12 )True )1 if label == '动作片' else 0 for label in all_labels])0 ].min () - 2 , X[:, 0 ].max () + 2 1 ].min () - 2 , X[:, 1 ].max () + 2 0.1 ),0.1 ))'#A0C4FF' , '#FFB3B3' ])'blue' , 'red' ]12 , 8 ))0 ], y=X[:, 1 ], hue=y, palette=cmap_bold, s=150 , edgecolor="k" )0 ], new_movie[1 ], c=final_color, s=300 , marker='*' ,f'未知电影 (被分类为{final_decision} )' , edgecolors='black' )f'kNN的决策边界 (K={k} )' , fontsize=18 )'爆炸场景数量' , fontsize=14 )'搞笑桥段数量' , fontsize=14 )'喜剧片' , '动作片' , f'未知电影 (被分类为{final_decision} )' ]12 )if __name__ == '__main__' :
SVM 支持向量机
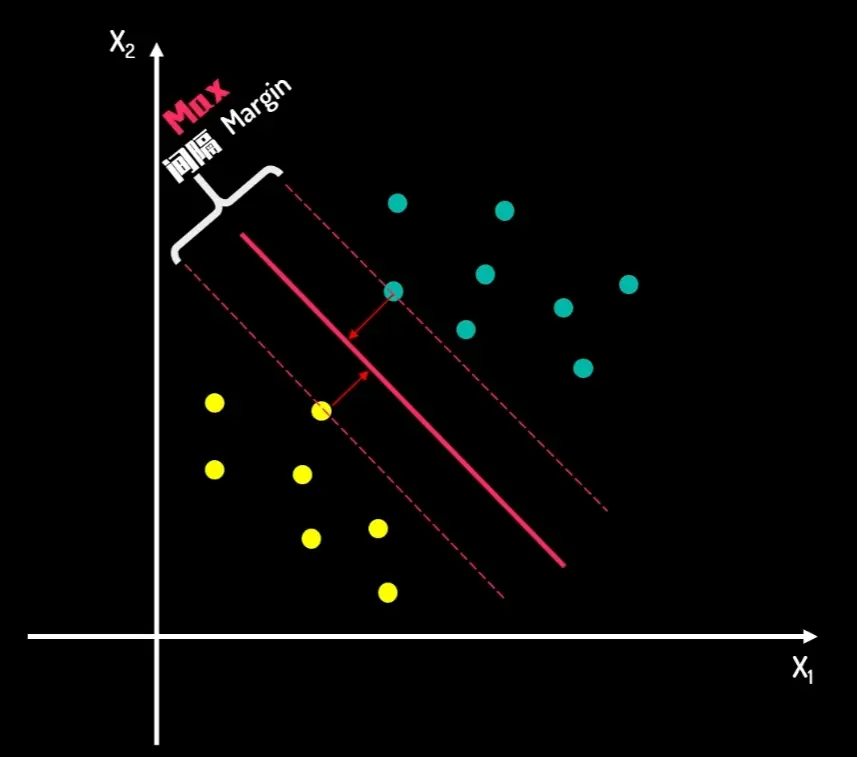
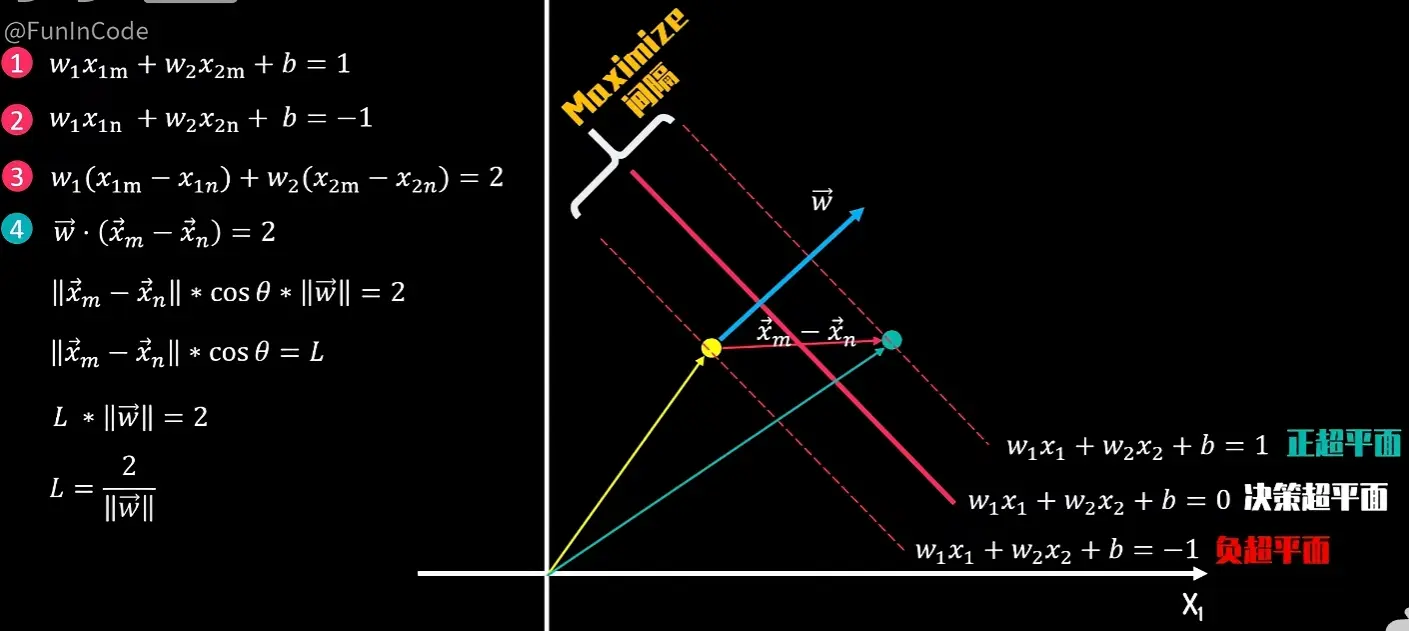
支持向量机是一种功能强大且用途广泛的监督学习算法,核心为不仅要找到一条能分开两类点的线(或更高维度的超平面 ),还要让这条线到两边数据点的**间隔(Margin)**尽可能宽,使得SVM具有很强的泛化能力,即对新数据的预测能力更强
超平面(Hyperplane) : 在二维空间里是一条直线 ,在三维空间里是一个平面 ,在更高维度的空间中,这个分界被称为超平面。它是决策的边界
间隔(Margin) :决策边界与离它最近的样本点之间的距离。SVM的目标就是最大化这个间隔
支持向量(Support Vectors) :那些离决策边界最近 的样本点(即图中分割线上的点),它们像“支撑”着整个决策边界一样,决定了间隔的宽度和超平面的最终位置。如果移动支持向量,超平面就会改变;如果移动其他非支持向量,超平面则不会受到影响。这是SVM高效的关键之一
硬间隔与软间隔:
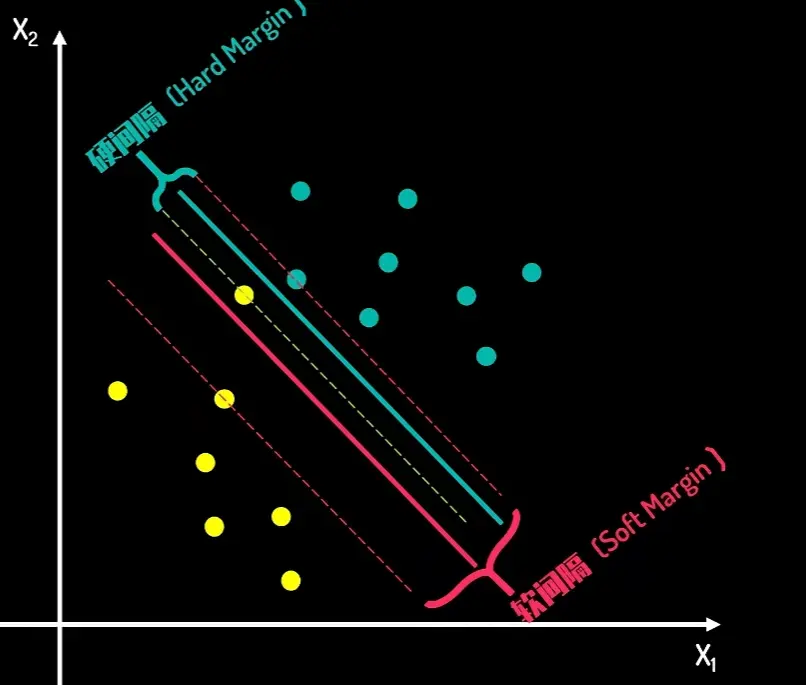
硬间隔完美分类所有点,同时最大化间隔,要求数据必须是完全线性可分 的
软间隔在最大化间隔和最小化分类错误之间找到平衡,可以处理非线性可分 或有噪声 的数据,鲁棒性更强
核心内容推导
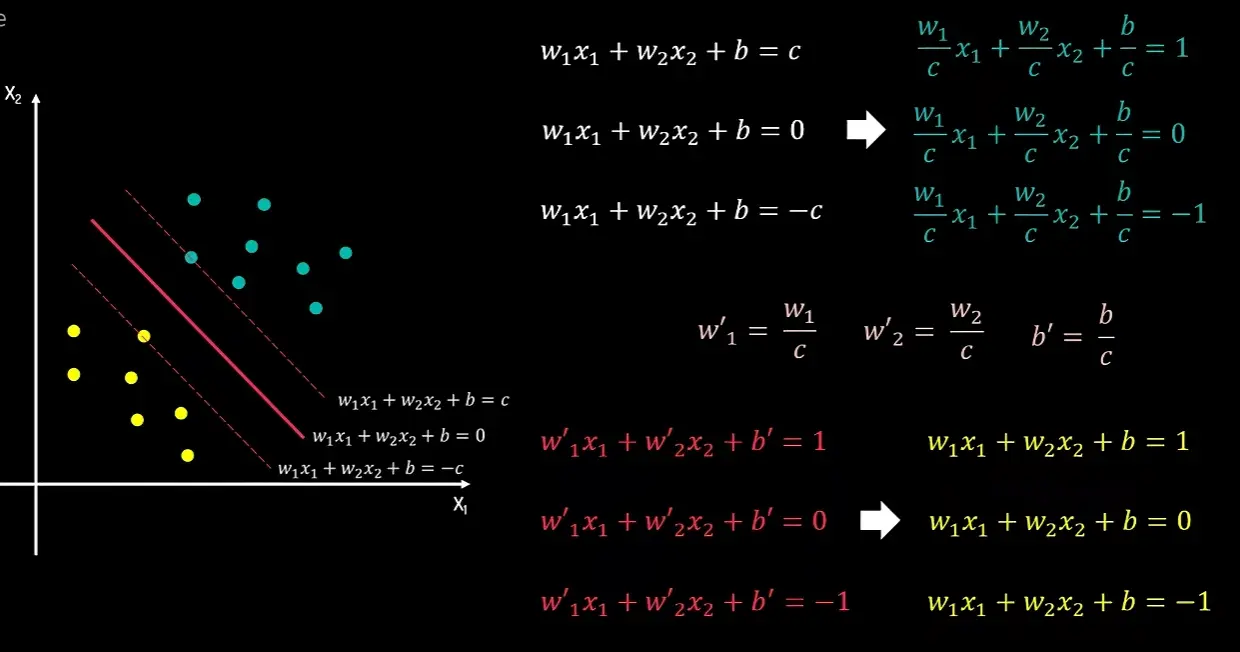
模型定义
优化目标:最大化间隔
硬间隔 的约束
其中
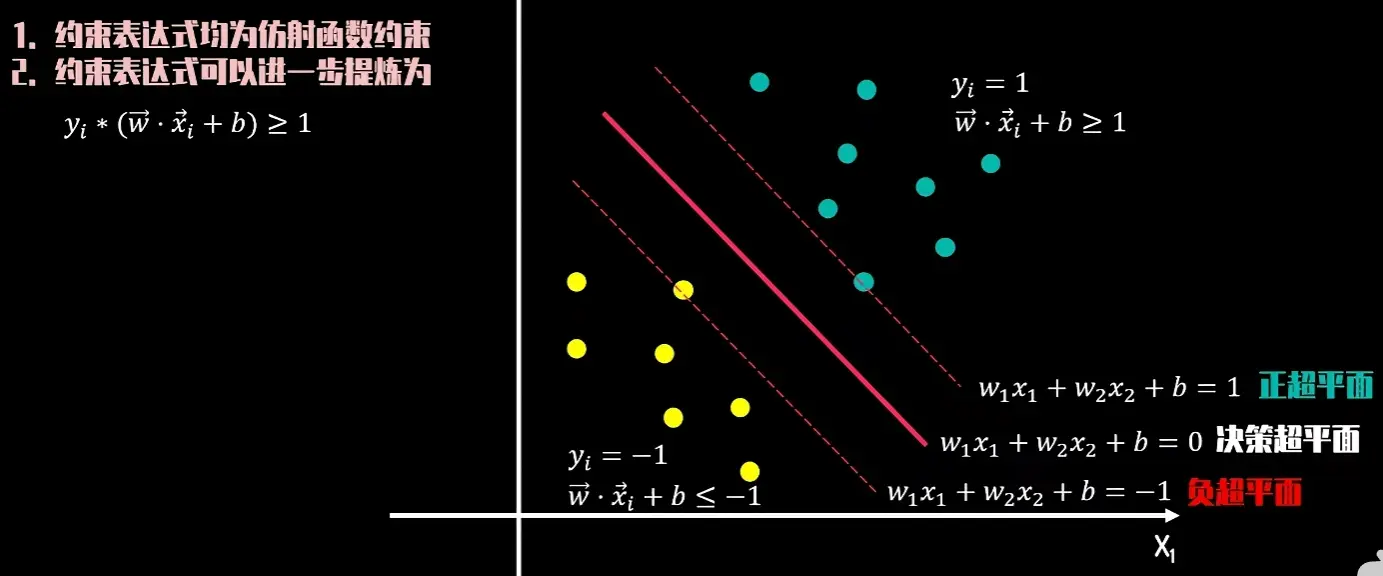
y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , … , N y_i(w \cdot x_i + b) - 1 \geq 0,\quad i = 1,\dots,N
y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , … , N
即为原始可行性条件(Primal Feasibility)
然后就得到了以下的模型定义,即优化问题,再构建拉格朗日函数
最后得到了硬间隔 的KKT 条件:
原始可行性条件(Primal Feasibility)
y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , … , N y_i\,(w \cdot x_i + b) - 1 \ge 0,\quad i = 1,\dots,N
y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , … , N
来源:SVM 原始优化问题的约束条件本身i i i y i ( w ⋅ x i + b ) y_i(w \cdot x_i + b) y i ( w ⋅ x i + b ) ≥ 1 \ge 1 ≥ 1
平稳性条件(Stationarity)
w − ∑ i = 1 N λ y i x i = 0 ⟹ w = ∑ i = 1 N λ i y i x i w - \sum_{i=1}^{N}\lambda y_i x_i = 0
\quad\Longrightarrow\quad
w = \sum_{i=1}^{N}\lambda_i y_i x_i
w − i = 1 ∑ N λ y i x i = 0 ⟹ w = i = 1 ∑ N λ i y i x i
来源:拉格朗日函数 L L L w w w ∂ L ∂ w = 0 \frac{\partial L}{\partial w}=0 ∂ w ∂ L = 0 w w w x i x_i x i α i \alpha_i α i α i > 0 \alpha_i>0 α i > 0 w w w
− ∑ i = 1 N λ i y i = 0 ⟹ ∑ i = 1 N λ i y i = 0 -\sum_{i=1}^{N}\lambda_i y_i = 0
\quad\Longrightarrow\quad
\sum_{i=1}^{N}\lambda_i y_i = 0
− i = 1 ∑ N λ i y i = 0 ⟹ i = 1 ∑ N λ i y i = 0
来源:拉格朗日函数 L L L b b b ∂ L ∂ b = 0 \frac{\partial L}{\partial b}=0 ∂ b ∂ L = 0
互补松弛条件(Complementary Slackness)
λ i [ y i ( w ⋅ x i + b ) − 1 ] = 0 , i = 1 , … , N \lambda_i\,\bigl[\,y_i(w \cdot x_i + b) - 1\,\bigr] = 0,\quad i = 1,\dots,N
λ i [ y i ( w ⋅ x i + b ) − 1 ] = 0 , i = 1 , … , N
来源:KKT 核心条件
情形 A: λ i = 0 \lambda_i = 0 λ i = 0 不是 支持向量,对决策边界无贡献;通常远离间隔边界且已正确分类情形 B: y i ( w ⋅ x i + b ) − 1 = 0 y_i(w \cdot x_i + b) - 1 = 0 y i ( w ⋅ x i + b ) − 1 = 0 λ i > 0 \lambda_i > 0 λ i > 0 支持向量(Support Vectors)
对偶可行性条件(Dual Feasibility)
λ i ≥ 0 , i = 1 , … , N \lambda_i \ge 0,\quad i = 1,\dots,N
λ i ≥ 0 , i = 1 , … , N
来源:拉格朗日乘子法对不等式约束的标准要求
对偶函数
构造下界函数q(λ),令该函数一定小于 目标函数的最小值,即 q ( λ ) ≤ f ( w ∗ ) q(\lambda) \leq f(w^*) q ( λ ) ≤ f ( w ∗ ) q(λ)最大值得到目标函数f ( w ∗ ) f(w^*) f ( w ∗ ) 最小值 的原问题转换成求最大值 的对偶问题
其中所有SVM问题(包括软&硬间隔)都是强对偶性 ,属于凸优化且满足斯莱特条件,因此max(q) = min(f)
将上述KKT条件全部代入后得到最终的对偶问题为:
核方法
当原数据难以被超平面划分时,可以通过升维 来提高区分度
**核技巧:**通过核函数直接计算出高维空间中的点积结果,从而避免对原始数据点进行升维计算
多项式核
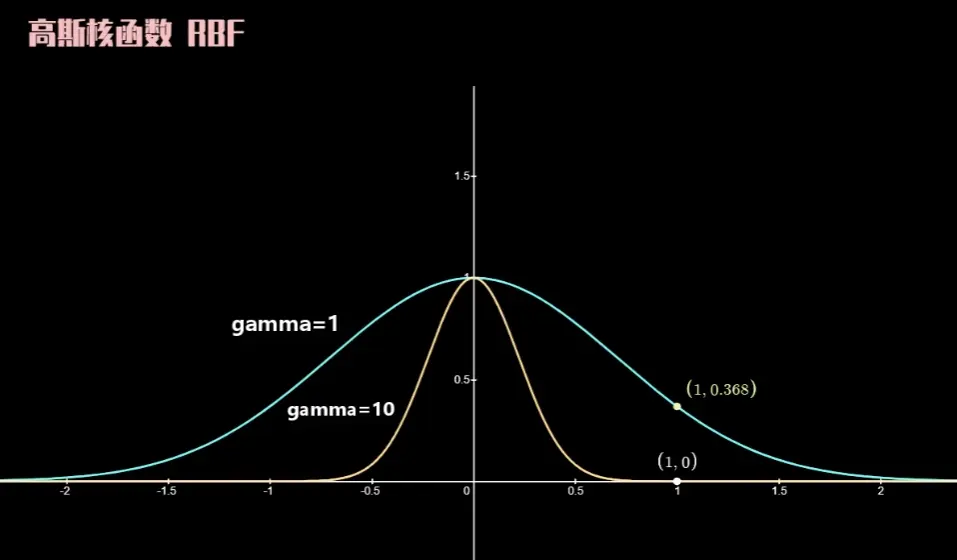
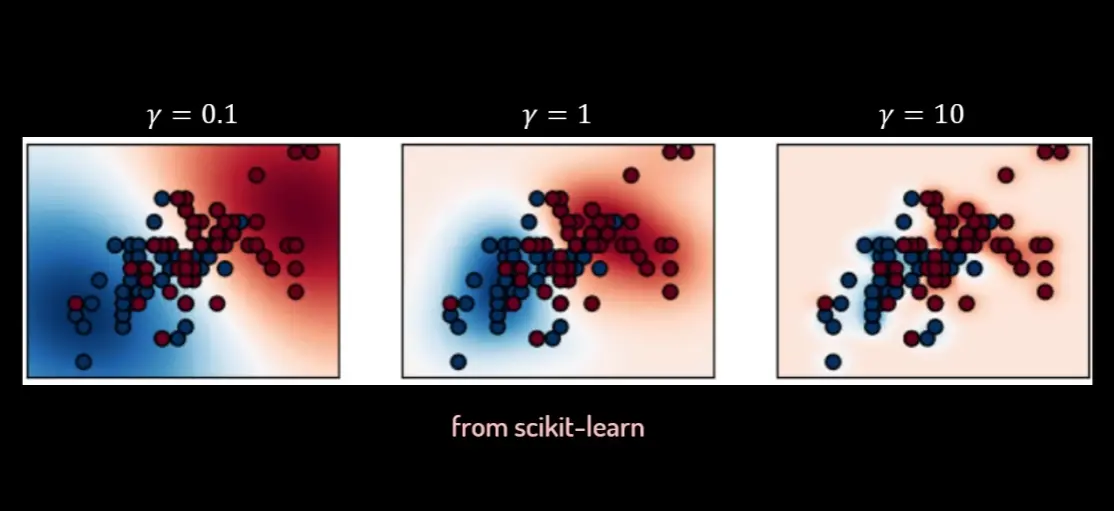
高斯核
K ( x ⃗ i , x ⃗ j ) = e − γ ∥ x ⃗ i − x ⃗ j ∥ 2 K(\vec{x}_i, \vec{x}_j) = e^{-\gamma \lVert \vec{x}_i - \vec{x}_j \rVert^2}
K ( x i , x j ) = e − γ ∥ x i − x j ∥ 2
其中 γ \gamma γ
对于SVM非线性分类,可以直接尝试使用高斯核
构建并求解核化的对偶问题
max λ q ( λ ) = ∑ i = 1 s λ i − 1 2 ∑ i = 1 s ∑ j = 1 s λ i λ j y i y j K ( x i ⃗ , x j ⃗ ) \max_{\boldsymbol{\lambda}} \quad q(\boldsymbol{\lambda}) = \sum_{i=1}^{s} \lambda_i - \frac{1}{2}\sum_{i=1}^{s}\sum_{j=1}^{s} \lambda_i \lambda_j y_i y_j K(\vec{x_i}, \vec{x_j})
λ max q ( λ ) = i = 1 ∑ s λ i − 2 1 i = 1 ∑ s j = 1 ∑ s λ i λ j y i y j K ( x i , x j )
约束条件 :
∑ i = 1 s λ i y i = 0 \sum_{i=1}^{s} \lambda_i y_i = 0 ∑ i = 1 s λ i y i = 0
0 ≤ λ i ≤ C ( 对于软间隔SVM ) 0 \le \lambda_i \le C \quad (\text{对于软间隔SVM}) 0 ≤ λ i ≤ C ( 对于软间隔 SVM )
获得最优解 λ i ∗ \lambda_i^* λ i ∗
将上述二次规划(QP)问题输入优化求解器,得到最优的拉格朗日乘子向量 λ ∗ = ( λ 1 ∗ , λ 2 ∗ , . . . , λ s ∗ ) \boldsymbol{\lambda}^* = (\lambda_1^*, \lambda_2^*, ..., \lambda_s^*) λ ∗ = ( λ 1 ∗ , λ 2 ∗ , ... , λ s ∗ )
计算偏置项 b b b
识别支持向量 (Support Vectors, SV)
根据求解出的 λ ∗ \boldsymbol{\lambda}^* λ ∗ λ i ∗ > 0 \lambda_i^* > 0 λ i ∗ > 0 x i ⃗ \vec{x_i} x i
选择一个边界上的支持向量
选择一个满足 0 < λ s ∗ < C 0 < \lambda_s^* < C 0 < λ s ∗ < C ( x s ⃗ , y s ) (\vec{x_s}, y_s) ( x s , y s )
计算 b b b
利用KKT条件 y s ( w ⃗ ⋅ ϕ ( x s ⃗ ) + b ) = 1 y_s (\vec{w} \cdot \phi(\vec{x_s}) + b) = 1 y s ( w ⋅ ϕ ( x s ) + b ) = 1 w ⃗ = ∑ i = 1 s λ i ∗ y i ϕ ( x i ⃗ ) \vec{w} = \sum_{i=1}^{s} \lambda_i^* y_i \phi(\vec{x_i}) w = ∑ i = 1 s λ i ∗ y i ϕ ( x i ) b b b b = y s − ∑ i ∈ SV λ i ∗ y i K ( x i ⃗ , x s ⃗ ) b = y_s - \sum_{i \in \text{SV}} \lambda_i^* y_i K(\vec{x_i}, \vec{x_s})
b = y s − i ∈ SV ∑ λ i ∗ y i K ( x i , x s )
为提高稳健性,实践中通常会计算所有边界支持向量的 b b b
决策函数
写出决策函数的形式
代入并使用核函数替换
将 w ⃗ \vec{w} w
f ( x ⃗ n e w ) = ( ∑ i ∈ SV λ i ∗ y i ϕ ( x i ⃗ ) ) ⋅ ϕ ( x ⃗ n e w ) + b f(\vec{x}_{new}) = \left( \sum_{i \in \text{SV}} \lambda_i^* y_i \phi(\vec{x_i}) \right) \cdot \phi(\vec{x}_{new}) + b
f ( x n e w ) = ( i ∈ SV ∑ λ i ∗ y i ϕ ( x i ) ) ⋅ ϕ ( x n e w ) + b
⇓ \Downarrow
⇓
f ( x ⃗ n e w ) = ∑ i ∈ SV λ i ∗ y i K ( x i ⃗ , x ⃗ n e w ) + b f(\vec{x}_{new}) = \sum_{i \in \text{SV}} \lambda_i^* y_i K(\vec{x_i}, \vec{x}_{new}) + b
f ( x n e w ) = i ∈ SV ∑ λ i ∗ y i K ( x i , x n e w ) + b
分类预测
Predicted Class = sign ( f ( x ⃗ n e w ) ) \text{Predicted Class} = \text{sign}(f(\vec{x}_{new}))
Predicted Class = sign ( f ( x n e w ))
如果 f ( x ⃗ n e w ) > 0 f(\vec{x}_{new}) > 0 f ( x n e w ) > 0
如果 f ( x ⃗ n e w ) < 0 f(\vec{x}_{new}) < 0 f ( x n e w ) < 0
软间隔
软间隔的优化目标
min w ⃗ , b , ξ 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + C ∑ i = 1 s ξ i \min_{\vec{w}, b, \boldsymbol{\xi}} \quad \frac{1}{2}||\vec{w}||^2 + C \sum_{i=1}^{s} \xi_i
w , b , ξ min 2 1 ∣∣ w ∣ ∣ 2 + C i = 1 ∑ s ξ i
y i ( w ⃗ ⋅ x i ⃗ + b ) ≥ 1 − ξ i y_i(\vec{w} \cdot \vec{x_i} + b) \ge 1 - \xi_i
y i ( w ⋅ x i + b ) ≥ 1 − ξ i
ξ i ≥ 0 , i = 1 , 2 , . . . , s \xi_i \ge 0, \quad i=1, 2, ..., s
ξ i ≥ 0 , i = 1 , 2 , ... , s
对偶问题与支持向量的变化
对偶问题的主要变化在于拉格朗日乘子 λ i \lambda_i λ i λ i ≥ 0 \lambda_i \ge 0 λ i ≥ 0
0 ≤ λ i ≤ C 0 \le \lambda_i \le C
0 ≤ λ i ≤ C
这个变化也丰富了支持向量(SV)的类型:
λ i = 0 \lambda_i = 0 λ i = 0 0 < λ i < C 0 < \lambda_i < C 0 < λ i < C ξ i = 0 \xi_i = 0 ξ i = 0 λ i = C \lambda_i = C λ i = C ξ i > 0 \xi_i > 0 ξ i > 0
其他内容与硬间隔相同
示例代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 import numpy as npimport matplotlib.pyplot as pltfrom sklearn import svm, datasetsfrom sklearn.preprocessing import StandardScaler'font.sans-serif' ] = ['SimHei' ] 'axes.unicode_minus' ] = False def plot_svm_boundary (clf, X, y, title ):""" 绘制SVM的决策边界、间隔和支持向量 """ .02 0 ].min () - 1 , X[:, 0 ].max () + 1 1 ].min () - 1 , X[:, 1 ].max () + 1 0.3 ) 'k' , levels=[-1 , 0 , 1 ], alpha=0.5 ,'--' , '-' , '--' ]) 0 ], X[:, 1 ], c=y, cmap=plt.cm.coolwarm, s=50 , edgecolors='k' )0 ], clf.support_vectors_[:, 1 ],100 , facecolors='none' , edgecolors='k' , linewidth=2 ,'Support Vectors' )'Feature 1' )'Feature 2' )'tight' )print ("正在生成线性SVM图..." )100 , centers=2 , random_state=6 )'linear' , C=1000 )8 , 6 ))'1. 线性SVM (趋向硬间隔)' )print ("正在生成软间隔SVM对比图..." )100 , centers=2 , random_state=0 , cluster_std=1.2 )'linear' , C=100 )'linear' , C=0.1 )12 , 6 ))1 , 2 , 1 )'2a. 软间隔 (高C值)' )1 , 2 , 2 )'2b. 软间隔 (低C值)' )print ("正在生成核函数SVM图..." )100 , factor=.5 , noise=.1 )'rbf' , C=1 , gamma='auto' )8 , 6 ))'3. 核函数SVM (RBF核)' )
蒙特卡洛方法
蒙特卡洛方法,又称随机抽样法或统计试验法,是一种依赖于重复随机抽样来获得数值结果的计算方法。其核心思想是将一个难以通过确定性算法求解的问题,转化为一个等价的概率模型,然后通过进行大量随机试验,利用统计学原理(如大数定律)来估算其解
例如在一个边长为2的正方形内部,画一个半径为1的内切圆,随机地向这个正方形内投掷大量的点,统计落在圆内的点的数量(N_circle)和落在正方形内的总点数(N_square),根据几何概率,圆的面积与正方形面积之比为 (π * 1²) / (2²) = π / 4。同时,这个比值约等于落在圆内的点数与总点数之比,即 N_circle / N_square。因此,可以推导出 π ≈ 4 * (N_circle / N_square)
核心原理
该方法的理论基础是概率论中的大数定律 :当样本数量足够大时,一个随机事件出现的频率会无限接近其真实概率。通过构造一个与问题解相关的随机试验,并进行海量重复,最终得到的统计平均值会收敛到问题的真实解
主要特点
依赖随机性 :使用伪随机数序列 (Pseudo-random Numbers) 来模拟随机过程概率收敛 :结果是统计意义上的近似解,伴随着一定的统计误差收敛速度 :误差收敛速度通常为 O ( 1 / N ) O(1/\sqrt{N}) O ( 1/ N ) N N N 通用性强 :概念简单,易于实现,并且能广泛应用于各种领域,尤其是那些本身就包含不确定性或维度极高的问题
优缺点与应用
优势 :实现简单,能够直观地模拟复杂的物理或金融过程,且其收敛速度与问题维度无关,能有效规避“维度灾难”。局限 :收敛速度相对较慢,获得高精度结果通常需要巨大的计算量典型应用 :粒子物理学(模拟粒子输运)、金融风险分析(VaR计算)、计算机图形学、项目管理风险评估、人工智能等
拟蒙特卡洛方法 (Quasi-Monte Carlo Method)
拟蒙特卡洛方法是蒙特卡洛方法的一种改进,旨在通过更优化的抽样策略来提高计算效率和精度。它并非采用纯粹的随机抽样,而是使用经过精心设计的、确定性的序列来更均匀地探索整个样本空间
核心原理
该方法用低差异序列 (Low-discrepancy Sequences) 取代了伪随机数。所谓“低差异”,指的是点集在空间中分布得非常均匀,系统性地避免了随机抽样中可能出现的点“聚集”和“空白”区域。这种均匀性使得用更少的样本点就能达到对整个样本空间的有效覆盖
主要特点
确定性序列 :使用哈尔顿 (Halton)、索博尔 (Sobol’) 等确定性的拟随机数序列均匀覆盖 :其设计目标是让样本点尽可能均匀地填充空间,新生成的点总会落在现有最“空旷”的位置收敛速度 :在理想条件下,其误差收敛速度可接近 O ( 1 / N ) O(1/N) O ( 1/ N ) 效率驱动 :专为提升数值积分和模拟的效率而设计
优缺点与应用
优势 :计算效率高,收敛速度快。在同样的计算成本下,通常能获得比标准蒙特卡洛方法精确得多的结果局限 :在处理极高维度问题时,低差异序列的均匀性优势可能会减弱。同时,由于其确定性,误差估计比标准蒙特卡洛方法更为复杂典型应用 :金融工程(尤其是期权定价)、高维数值积分、计算机图形学(全局光照渲染)等对计算精度和速度要求都非常高的领域
马尔科夫链
从本质上讲,马尔科夫链是一个数学模型,它通过一系列概率来描述一个系统如何从一个状态演变到另一个状态,下一步的状态只与当前状态有关
马尔科夫性质 (Markov Property)
这是马尔科夫链得以简化复杂现实问题的关键,即**“无记忆性” (Memorylessness)**
定义 : 系统在 t + 1 t+1 t + 1 t t t t t t
P ( X n + 1 = j ∣ X n = i , X n − 1 = i n − 1 , . . . , X 0 = i 0 ) = P ( X n + 1 = j ∣ X n = i ) P(X_{n+1} = j | X_n = i, X_{n-1} = i_{n-1}, ..., X_0 = i_0) = P(X_{n+1} = j | X_n = i)
P ( X n + 1 = j ∣ X n = i , X n − 1 = i n − 1 , ... , X 0 = i 0 ) = P ( X n + 1 = j ∣ X n = i )
如明天的天气怎么样,只和今天的天气状况有关,而和昨天、前天的天气没有直接关系。虽然这在现实中是过度简化,但它为我们提供了一个强大且可计算的分析框架
定义
状态 (State) 与状态空间 (State Space)
状态 : 系统在某个瞬间的快照。它可以是任何离散的情况状态空间 (S S S : 系统所有可能状态的集合示例 :
天气模型 : 状态空间 S = { 晴天, 阴天, 雨天 } S = \{\text{晴天, 阴天, 雨天}\} S = { 晴天 , 阴天 , 雨天 }
转移概率 (Transition Probability) 与转移矩阵 (P P P
系统从一个状态到另一个状态的可能性。这些概率被组织在一个称为转移矩阵 P P P 的方阵中
矩阵元素 : p i j p_{ij} p ij i i i 经过一步 转移到状态 j j j
示例:三状态天气模型
如果今天晴天,明天有80%概率继续晴天,20%概率变阴天,0%概率下雨
如果今天阴天,明天40%概率转晴,40%概率继续阴天,20%概率下雨
如果今天雨天,明天60%概率转晴,30%概率变阴天,10%概率继续下雨
对应的转移矩阵 P P P
P = ( 0.8 0.2 0.0 0.4 0.4 0.2 0.6 0.3 0.1 ) P = \begin{pmatrix}
0.8 & 0.2 & 0.0 \\
0.4 & 0.4 & 0.2 \\
0.6 & 0.3 & 0.1
\end{pmatrix}
P = 0.8 0.4 0.6 0.2 0.4 0.3 0.0 0.2 0.1
矩阵性质 :
非负性 : p i j ≥ 0 p_{ij} \ge 0 p ij ≥ 0 行和为1 : ∑ j p i j = 1 \sum_{j} p_{ij} = 1 ∑ j p ij = 1
1. n阶转移矩阵 (P ( n ) P^{(n)} P ( n )
描述系统经过 n 步 转移的概率矩阵,即P ( n ) = P n P^{(n)} = P^n P ( n ) = P n
2. 切普曼-柯尔莫哥洛夫方程 (Chapman-Kolmogorov Equation)
公式 : P ( m + n ) = P ( m ) P ( n ) P^{(m+n)} = P^{(m)} P^{(n)} P ( m + n ) = P ( m ) P ( n ) 解释 : 从状态 i i i m + n m+n m + n j j j m m m i i i k k k n n n k k k j j j k k k
链的分类与状态的性质
1. 可约性 (Reducibility)
不可约 (Irreducible) : 链中任意两个状态都是互通 的(可以相互到达)。系统像一个设计良好的城市,所有地点之间都有路径
示例 : 上述天气模型就是不可约的,你可以从任何天气类型最终转到任何其他天气类型
可约 (Reducible) : 链中存在不互通的状态。系统内部存在“孤岛”或“陷阱”
2. 周期性 (Periodicity)
3. 状态类型
常返态 (Recurrent State) : 只要离开,最终总能100%回来瞬时态 (Transient State) : 离开后,有一定的概率再也回不来了在上面可约的游戏示例中,状态2和3是常返态 (甚至是吸收态)。状态1是瞬时态 ,因为只要离开状态1,就再也回不来了。
4. 平稳分布 (Stationary Distribution)
当一个马尔科夫链运行足够长时间后,系统处于各个状态的概率将不再随时间变化,达到一种统计上的平衡。这个平衡时的概率分布,就是平稳分布 π \pi π
π P = π \pi P = \pi
π P = π
约束:∑ j π j = 1 \sum_j \pi_j = 1 ∑ j π j = 1
平稳分布向量π \pi π
当前的概率分布 π \pi π π \pi π
对于一个有限状态、不可约、非周期 的马尔科夫链,存在唯一 的平稳分布 π \pi π
与极限矩阵的关系:
对于满足上述黄金定理的链,当 n → ∞ n \to \infty n → ∞ P ( n ) P^{(n)} P ( n ) W W W
这个矩阵的每一行,就是那个唯一的平稳分布向量 π \pi π
深刻含义 : 经过足够长的时间,系统遗忘了它的初始状态 。无论一开始是晴天、阴天还是雨天,在遥远的未来,是晴天的概率都会趋近于同一个值 π 1 \pi_1 π 1 示例(续) :对于我们的天气模型,可以解出其唯一平稳分布约为 π ≈ ( 0.655 , 0.259 , 0.086 ) \pi \approx (0.655, 0.259, 0.086) π ≈ ( 0.655 , 0.259 , 0.086 )
HMM 隐马尔可夫模型
隐马尔可夫模型 (Hidden Markov Model, HMM) 是标准马尔科夫链的扩展,用于解决状态不可观测 的问题。它描述了这样一个过程:系统内部存在一个不可见的、隐藏的马尔科夫状态链,而我们只能观测到由这些隐藏状态以一定概率生成的输出序列。HMM的目标就是通过可观测的序列,来推断隐藏状态的性质和序列
示例:密室天气
隐藏状态 (Hidden State) : 你无法直接看到的真实天气(如:晴天、雨天)。它的变化遵循一个马尔科夫过程观测值 (Observation) : 你能看到的表象(如:进屋的人的心情)。某个观测值的出现概率与当时的隐藏状态有关
HMM 的五大组成要素
一个完整的HMM模型由一个五元组 λ = ( S , O , A , B , π ) \lambda = (S, O, A, B, \pi) λ = ( S , O , A , B , π )
隐藏状态集合 S S S :
所有可能的隐藏状态的集合
S = { s 1 , s 2 , . . . , s N } S = \{s_1, s_2, ..., s_N\} S = { s 1 , s 2 , ... , s N } N N N
观测集合 O O O :
所有可能的观测值的集合。
O = { o 1 , o 2 , . . . , o M } O = \{o_1, o_2, ..., o_M\} O = { o 1 , o 2 , ... , o M } M M M
状态转移概率矩阵 A A A :
描述隐藏状态之间 的转移概率,与标准马尔科夫链的转移矩阵相同
A = [ a i j ] A = [a_{ij}] A = [ a ij ] a i j = P ( 下一时刻为状态 s j ∣ 当前为状态 s i ) a_{ij} = P(\text{下一时刻为状态 } s_j | \text{当前为状态 } s_i) a ij = P ( 下一时刻为状态 s j ∣ 当前为状态 s i )
发射概率矩阵 B B B :
描述在某个隐藏状态 下,生成某个观测值 的概率。这是HMM特有的核心
B = [ b j ( k ) ] B = [b_j(k)] B = [ b j ( k )] b j ( k ) = P ( 观测到 o k ∣ 当前为状态 s j ) b_j(k) = P(\text{观测到 } o_k | \text{当前为状态 } s_j) b j ( k ) = P ( 观测到 o k ∣ 当前为状态 s j )
初始状态概率分布 π \pi π :
描述系统在初始时刻处于各个隐藏状态 的概率
π = [ π i ] \pi = [\pi_i] π = [ π i ] π i = P ( 初始时刻为状态 s i ) \pi_i = P(\text{初始时刻为状态 } s_i) π i = P ( 初始时刻为状态 s i )
HMM 的三大应用
HMM的强大之处在于它能系统性地解决以下三个核心问题:
问题类型
问题描述
解决方法
评估问题 (Evaluation) 给定模型 λ \lambda λ O O O
\lambda)$
解码问题 (Decoding) 给定模型 λ \lambda λ O O O 最有可能 产生此观测的隐藏状态序列 Q Q Q
维特比算法 (Viterbi Algorithm)
学习问题 (Learning) 仅给定观测序列 O O O λ = ( A , B , π ) \lambda=(A, B, \pi) λ = ( A , B , π )
鲍姆-韦尔奇算法 (Baum-Welch Algorithm)